Abstract
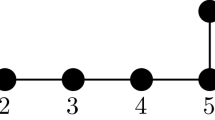
Borcherds algebras represent a new class of Lie algebras which have almost all the properties that ordinary Kac-Moody algebras have, but the only major difference is that these generalized Kac-Moody algebras are allowed to have imaginary simple roots. The simplest nontrivial examples one can think of are those where one adds ‘by hand’ one imaginary simple root to an ordinary Kac-Moody algebra. We study the fundamental representation of this class of examples and prove that an irreducible module is given by the full tensor algebra over some integrable highest weight module of the underlying Kac-Moody algebra. We also comment on possible realizations of these Lie algebras in physics as symmetry algebras in quantum field theory.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Borcherds, R. E., Vertex algebras, Kac-Moody algebras, and the monster,Proc. Nat. Acad. Sci. USA,83, 3068–3071 (1986).
Borcherds, R. E., Monstrous Lie superalgebras,Invent. Math. 109, 405–444 (1992).
Gebert, R. W., Introduction to vertex algebras, Borcherds algebras, and the monster Lie algebra.Internat. J. Modern Phys. A 8, 5441–5503 (1993).
Conway, J. H., The automorphism group of the 26-dimensional even unimodular Lorentzian lattice,J. Algebra 80, 159–163 (1983).
Borcherds, R. E., Conway, J. H., Queen, L., and Sloane, N. J. A., A monster Lie algebra?Adv. in Math. 53, 75–79 (1984).
Frenkel, I. B., Representations of Kac-Moody algebras and dual resonance models, inApplications of Group Theory in Theoretical Physics, Lect. Appl. Math., Vol. 21. Amer. Math. Soc., Providence, 1985, pp. 325–353.
Goddard, P. and Olive, D., Algebras, lattices and strings, in J. Lepowsky, S. Mandelstam, and I. M. Singer (eds),Vertex Operators in Mathematics and Physics - Proc. Conference, November 10-17, 1983, Publ. Math. Sci. Res. Inst. #3, Springer, New York, 1985, pp. 51–96.
Borcherds, R. E., The monster Lie algebra,Adv. in Math. 83, 30–47 (1990).
Borcherds, R. E., Generalized Kac-Moody algebras,J. Algebra 115, 501–512 (1988).
Harada, K., Miyamoto, M., and Yamada, H. A generalization of Kac-Moody algebras, Preprint.
Borcherds, R. E., Central extensions of generalized Kac-Moody algebras,J. Algebra 140, 330–335 (1991).
Slansky, R., An algebraic role for energy and number operators for multiparticle states. Preprint LA-UR-91-3562, Los Alamos National Laboratory, 1991.
Kac, V. G.,Infinite Dimensional Lie Algebras, Cambridge University Press, Cambridge, third edition, 1990.
Gepner, D. and Witten, E., String theory on group manifolds,Nuclear Phys. B 278, 493–549 (1986).
Author information
Authors and Affiliations
Additional information
Supported by Konrad-Adenauer-Stiftung e.V.
Supported by Deutsche Forschungsgemeinschaft.
Rights and permissions
About this article
Cite this article
Gebert, R.W., Teschner, J. On the fundamental representation of borcherds algebras with one imaginary simple root. Lett Math Phys 31, 327–334 (1994). https://doi.org/10.1007/BF00762796
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00762796