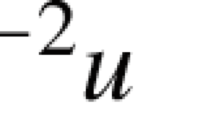Skip to main content
SpringerLink
Log in

On Darboux transformations for soliton equations in high-dimensional spacetime

  • Published:
Letters in Mathematical Physics Aims and scope Submit manuscript

Abstract

The Darboux transformations for a class of completely integrable systems in the spacetimeR n + 1, which are much more general than the systems inLett. Math. Phys. 26, 199–209 (1989), are considered. The structure of the nonlinear evolution equations with space constraints is elucidated. It is pointed out that the inverse scattering method can be used to solve the Cauchy problem with initial data given on a noncharacteristic line.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ablowitz, M. J., Beals, R., and Tenenblat, K., On the solution of the generalized wave and generalized sine-Gordon equation,Stud. Appl. Math. 74, 177 (1986).

    Google Scholar 

  2. Beals, R. and Coifman, R. R., Scattering and inverse scattering for first order systems,Comm. Pure Appl. Math. 37, 39 (1984).

    Google Scholar 

  3. Beals, R. and Coifman, R. R., Inverse scattering and evolution equations,Comm. Pure Appl. Math. 38, 29 (1985).

    Google Scholar 

  4. Cheng, Y., Constraint of integrable systems: From higher to lower dimensions,Phys. Lett. A166, 217 (1992).

    Google Scholar 

  5. Gu, C. H., On the Darboux form of Bäcklund transformations, inIntegrable System, Nankai Lectures on Math. Phys., World Scientific, Singapore, 1989, pp. 162–168.

    Google Scholar 

  6. Gu, C. H., Darboux transformations for a class of integrable systems inn variables, to appear inColloque International, Analyse, Variétés et Physique, 1992.

  7. Gu, C. H., On the interaction of solitons for a class of integrable systems in the spacetimeR n + 1,Lett. Math. Phys. 26, 199–209 (1992).

    Google Scholar 

  8. Konopelchenko, B., Sidorenko, J., and Strampp, W., (1 + 1)-dimensional integrable systems as symmetry constraints of (2 + 1) dimensional systems,Phys. Lett. A157, 17 (1991).

    Google Scholar 

  9. Sattinger, D. H. and Zurkowski, V. D., Gauge theory of Bäcklund transformations II,Physica 26D, 225 (1987).

    Google Scholar 

  10. Wilson, G., Commuting flows and conservation laws for Lax equations,Math. Proc. Camb. Phil. Soc. 86, 131 (1979).

    Google Scholar 

  11. Zhou, Z. X., Explicit Solutions of N-Wave Equation in 1 + 2 Dimensions,Phys. Lett. A168, 370 (1992).

    Google Scholar 

  12. Zhou, Z. X., A method to obtain explicit solutions of 1 + 2 dimensional AKNS system,Internat. J. Modern Phys. A 3, 565 (1993).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Science and Technology of China, Hefei, China

    Gu Chaohao

  2. Institute of Mathematics, Fudan University, Shanghai, China

    Gu Chaohao

  3. Institute of Mathematics, Fudan University, Shanghai, China

    Zhou Zixiang

Authors
  1. Gu Chaohao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhou Zixiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Supported by National Basic Research Project ‘Nonlinear Science’, NNSFC of China, FEYUT-SEDC-CHINA and Fok Ying-Tung Education Foundation of China.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chaohao, G., Zixiang, Z. On Darboux transformations for soliton equations in high-dimensional spacetime. Lett Math Phys 32, 1–10 (1994). https://doi.org/10.1007/BF00761119

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00761119

Mathematics Subject Classifications (1991)

Search

Navigation