Abstract
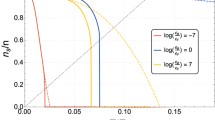
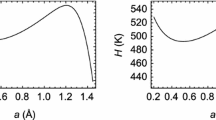
We consider the properties of vortices in superfluid helium-4 at negative pressure. Based on a simple density-functional model, we first calculate the density profile in the vicinity of a vortex. We then determine the negative pressure at which the vortex becomes unstable against a uniform radial expansion all along its length. This instability occurs at −6.9 bars. We then calculate the pressure-dependence of the energy Δ Enuc required to nucleate a bubble on the vortex. The results of this calculation are used to estimate the effect of quantized vortices on the rate at which bubbles are nucleated in superfluid helium at negative pressure.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Early measurements were made by J. W. Beams,Phys. Rev. 104, 880 (1956), and A. D. Misener and G. R. Herbert,Nature 177, 946 (1956).
J. C. Fisher,J. Appl. Phys. 19, 1062 (1948).
H. J. Maris and Q. Xiong,Phys. Rev. Lett. 63, 1078 (1989).
Q. Xiong and H. J. Maris,J. Low Temp. Phys. 77, 347 (1989).
R. D. Finch, R. Kagiwada, M. Barmatz, and I. Rudnick,Phys. Rev. 134 A1425 (1964).
R. D. Finch and T. G. Wang,J. Acoust. Soc. Am. 39, 511 (1966).
R. D. Finch, T. G. Wang, R. Kagiwada, M. Barmatz, and I. Rudnick,J. Acoust. Soc. Am. 40, 211 (1966).
M. H. Edwards, R. M. Cleary, and W. M. Fairbank, inQuantum Fluids (North-Holland, Amsterdam, 1966), p. 140.
R. D. Finch and M. L. Chu,Phys. Rev. 161, 202 (1967).
P. D. Jarman and K. J. Taylor,J. Low Temp. Phys. 2, 389 (1970).
P. M. McConnell, M. L. Chu, and R. D. Finch,Phys. Rev. 1, 411 (1970).
A. Mossé, M. L. Chu, and R. D. Finch,J. Acoust. Soc. Am. 47, 1258 (1970).
E. A. Neppiras and R. D. Finch,J. Acoust. Soc. Am. 52, 335 (1971).
J. R. Shadley and R. D. Finch,Phys. Rev. A 3, 780 (1971).
P. L. Marston,J. Low Temp. Phys. 25, 383 (1976).
H. C. Dhingra and R. D. Finch,J. Acoust. Soc. Am. 59, 19 (1976).
D. E. Daney,Cryogenics 28, 132 (1988).
J. A. Nissen, E. Bodegom, L. C. Brodie, and J. S. Semura,Adv. Cryo. Engineering 33, 999 (1988);Phys. Rev. B 40, 617 (1989).
Q. Xiong and H. J. Maris,J. Low Temp. Phys. 82, 105 (1991).
V. A. Akulichev and Y. Y. Boguslavskii,Sov. Phys. JETP 35, 1012 (1972).
R. B. Dean,J. Appl. Phys. 15, 446 (1944).
F. Dalfovo, G. Renversez, and J. Treiner,J. Low Temp. 89, 425 (1992).
F. Dalfovo,Phys. Rev. B 46, 5482 (1992).
B. M. Abraham, Y. Eckstein, J. B. Ketterson, M. Kuchnir, and P. R. Roach,Phys. Rev. A 1, 250 (1970).
W. M. Whitney and C. E. Chase,Phys. Rev. Lett. 9, 243 (1962).
H. J. Maris,Phys. Rev. Lett. 66, 45 (1991).
H. J. Maris, in “Excitations in Liquid Helium at Negative Pressures,” inNato Advanced Research Workshop on Excitations in 2D and 3D Quantum Fluids edited by H. J. Lauter and A. F. G. Wyatt (Plenum, New York, 1991), p. 107.
J. R. Eckardt, D. O. Edwards, S. Y. Shen, and F. M. Gasparini,Phys. Rev. B 16, 1944 (1977).
M. Iino, M. Suzuki, and A. Ikushima,J. Low Temp. Phys. 61, 155 (1985).
C. Ebner and W. F. Saam,Phys. Rev. Phys. Rev. B 12, 923 (1975).
L. B. Lurio, T. A. Rabedeau, P. S. Pershan, I. F. Silvera, M. Deutsch, S. D. Kosowsky, and B. M. Ocko,Phys. Rev. Lett. 68, 2628 (1992).
Using the earlier version of the equation of state we had obtained the value of −6.5 bars for Pv. See Ref. 4..
Using a more elaborate density-functional scheme F. Dalfovo has obtained the value −8 bars forP v. See Ref. 24..
For an example of the use of this model see Ref. 23..
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Maris, H.J. Nucleation of Bubbles on quantized vortices in helium-4. J Low Temp Phys 94, 125–144 (1994). https://doi.org/10.1007/BF00755421
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00755421