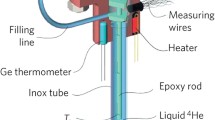
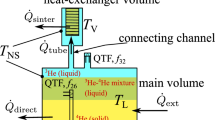
Abstract
New measurements of the boundary resistivity in superfluid4He (2ppb3He) nearT λ are reported as a function of ¦ɛ¦ (ɛ =T/T λ(Q) — 1) and of heat flux Q in a cell with parallel polished copper surfaces. Here we call Tλ(Q) the temperature where the superfluid state abruptly disappears. In this design, the sidewall gaps between the copper pieces and the stainless steel spacer were eliminated. In contrast to several previous experiments but in agreement with those of Li and Lip a, no largeQ-dependent boundary resistivity anomaly was detected. However, as ¦ɛ¦ → 0 the small weakly divergent resistivity was observed and its dependence onQ over the experimental range 1 <Q < 80 μW/cm2 was found to be very small. These new results are compared with previous experiments and predictions. An explanation of the previously observed anomalous transport phenomena is presented in terms of a heat flow through the sidewall gaps in these cells, and its limitation by a critical flow value Φc. This phenomenological model can be fit satisfactorily to the observations. In the appendix we calculate Φc from mutual friction.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. V. Duncan, G. Ahlers, and V. Steinberg,Phys. Rev. Lett. 58, 377 (1987).
R. V. Duncan and G. Ahlers,Phys. Rev. B 43, 7707 (1991).
D. Frank and V. Dohm,Phys. Rev. Lett. 62, 1864 (1989) andZ. Phys. B 84, 443 (1991). A complete list of references to previous work on the singularity ofR K is given in the 2nd paper.
R. A. Ferrell,Physica B 165/166, 557 (1990). This author has also made quantitative predictions of the divergence of the boundary resistivity. This divergence is roughly proportional to |ɛ|2/3, stronger than that predicted by Ref. 3 and measured by Duncanetal. 1,2.
F. Zhong, J. Tuttle, and H. Meyer,J. Low Temp. Phys. 79, 9 (1990).
D. Murphy and H. Meyer,J. Low Temp. Phys. 97, 489 (1994).
J. S. Olafsen and R. P. Behringer,Phys. Rev. B 52, 61 (1995) and to be published. These authors measured the thermal response ΔT(ω) across a layer of superfluid4He to an AC heat flux, which gaveR b . Their measurements indicated the existence of both aQ-dependent value forR b and an unexpected frequency dependence for |ɛ| <3 × 10−3.
W. Y. Tarn and G. Ahlers,Phys. Rev. B 32, 5932 (1985).
M. Dingus, F. Zhong, and H. Meyer,J. Low Temp. Phys. 65, 185 (1986).
Q. Li, Ph.D Thesis, Stanford University (1990) (unpublished). J. Lipa (private communication).
F.-C. Liu and G. Ahlers,Phys. Rev. Lett. 76, 1300 (1996).
D. Murphy and H. Meyer,J. Low Temp. Phys. 99, 745 (1995).
R. V. Duncan, Ph.D thesis, University of California at Santa Barbara (1988).
D. S. Greywall and G. Ahlers,Phys. Rev. A 7, 2145 (1973).
A discussion of the Vinen equation,Proc. R. Soc. London Sect. A 242, 493 (1957) as modified by Schwarz,Phys. Rev. B 18, 245 (1978), is presented in the paper by Ladner and Tough16
D. R. Ladner and J. T. Tough,Phys. Rev. B 20, 2690 (1979).
J. R. Clow and J. D. Reppy,Phys. Rev. Lett. 19, 291 (1967);Phys. Rev. A 5, 424 (1972).
S. V. Iordanskii,JETP,21, 467, (1965).
J. S. Langer and M. E. Fisher,Phys. Rev. Lett. 19, 560 (1967).
R. Haussmann and V. Dohm,Phys. Rev. B 46, 6361 (1992).
A. Onuki, private communication.
J. T. Tough, “Superfluid Turbulence,” in Progress in Low Temperature Physics, VIII, ed. D. F. Brewer, North Holland Publishing Co. (1982).
P. Leiderer and F. Pobell,J. Low Temp. Phys. 3, 577 (1970). The mutual friction coefficienta = 560 in their work has been multiplied byT −35λ to give oura MF the same units asA.
D. Murphy and H. Meyer, (to be published).
It has been shown by K. W. Schwarz,Phys. Rev. B 38, 2398 (1988) that the Vinen model needs corrections. Nevertheless we use the model as presented by Tough22 in our crude approximative treatment, the purpose of which is simply to explain a phenomenon, not to determine new properties in a precise manner.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Murphy, D., Meyer, H. Thermal boundary resistance in superfluid4He nearT λ . J Low Temp Phys 105, 185–209 (1996). https://doi.org/10.1007/BF00754633
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00754633