Skip to main content
SpringerLink
Log in

Analysis of laminar flow forced convection heat transfer in the entrance region of a circular pipe

  • Published:
Wärme- und Stoffübertragung Aims and scope Submit manuscript

Abstract

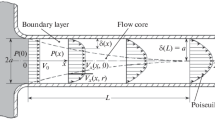
A numerical solution, for incompressible, steady-state, laminar flow heat transfer in the combined entrance region of a circular tube is presented for the case of constant wall heat flux and constant wall temperature. The development of velocity profile is obtained from Sparrow's entrance region solution. This velocity distribution is used in solving the energy equation numerically to obtain temperature profiles. Variation of the heat transfer coefficient for these two different boundary conditions for the early stages of boundary layer formation on the pipe wall is obtained. Local Nusselt numbers are calculated and the results are compared with those given byUlrichson andSchmitz. The effect of the thermal boundary conditions is studied by comparing the uniform wall heat flux results with uniform wall temperature.

Zusammenfassung

Für inkompressible, stationäre, laminare Rohrströmung wird der Wärmeübergang im gemeinsamen Einlauf für konstante Wärmestromdichte und konstante Wandtemperatur numerisch berechnet. Die Entwicklung der Geschwindigkeitsprofile wird einer Lösung vonSparrow entnommen, mit deren Hilfe die Temperaturprofile berechnet werden. Hieraus erhält man den Verlauf des Wärmeübergangskoeffizienten am Beginn der Grenzschichtbildung. Die berechneten örtlichen Nusselt-Zahlen werden mit jenen nachUlrichson undSchmitz verglichen. Die Wirkung der thermischen Grenzschicht wird durch Vergleich der Ergebnisse für konstante Wärmestromdichte mit jenen für konstante Wandtemperatur untersucht.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

Surface area, m2

C p :

Specific heat at constant pressure, kcal/kg grd

J 0 :

Zero order Bessel functions of the first kind

T :

Temperature, °C

d :

Diameter of pipe, m

k :

Thermal conductivity, kcal/m h grd

m :

Number of increment inx direction

n :

Number of increment iny direction

q/A :

Heat flow rate per unit area, kcal/h m2

r :

Radial distance measured from centre of pipe, m

r 0 :

Radius of pipe, m

u :

Local axial velocity component, m/s

ū :

Average axial velocity, m/s

v :

Local radial velocity component, m/s

x :

Axial coordinate measured from inlet of pipe

x*:

Axial stretched coordinate measured from inlet of pipe

y :

Radial distance measured from pipe wall

ΔX, ΔY :

Dimensionless increments in axial and radial directions

Nu (=hd/k):

Nusselt number

Pr (=μC p/k):

Prandtl number

Re (=ūd/v):

Reynolds number

U (=u/ū):

Dimensionless velocity

X (=4x/d/Re):

Dimensionless axial coordinate

Y (=y/d):

Dimensionless radial coordinate

θ:

Fluid density, kg/m3

β:

Eigenvalues

μ:

Dynamic viscosity, kg/m·s

ν:

Kinematic viscosity, m2/s

b:

Refers to bulk, or mixed mean temperature

i:

inlet

w:

surface

T:

constant wall temperature boundary condition

q :

constant heat flux boundary condition

References

  1. Ulrichson, D. L., andR. A. Schmitz: Int. J. Heat Mass Transfer Vol. 8 (1965) pp. 253/258.

    Article  Google Scholar 

  2. Roy, D. N.: Trans. ASME, J. of Heat Transfer Vol. 98 (1965) p. 425.

    Article  Google Scholar 

  3. Kays, W. M.: Trans. Am. Soc. Mech. Engrs. 77 (1955) pp. 1265/1274.

    Google Scholar 

  4. Heaton, H. S., W. C. Reynolds andW. M. Kays: Rep. No. AHT-5, Thermosciences Division, Dept. of Mech. Engng. Stanford University. Stanford (1962).

  5. Basworth, R. T., andH. C. Ward: Paper no. 169, presented at the Annual Meeting of the Amer. Inst. Chem. Engrs. Chicago (1962).

  6. Manohar, R.: Int. J. Heat Mass Transfer Vol. 12 (1969).

  7. Sparrow, E. M., S. H. Lin andT. S. Lundgren: The Physics of Fluids, Vol. 7 (1964) No. 3,

  8. Jeffreys, S. H., andB. S. Jeffreys: Methods of Mathematical Physics, Cambridge Press 1962.

Download references

Author information

Authors and Affiliations

  1. Ankara

    S. Kakaç & M. R. Özgü

Authors
  1. S. Kakaç
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. R. Özgü
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kakaç, S., Özgü, M.R. Analysis of laminar flow forced convection heat transfer in the entrance region of a circular pipe. Wärme- und Stoffübertragung 2, 240–245 (1969). https://doi.org/10.1007/BF00751357

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00751357

Keywords

Search

Navigation