Conclusions
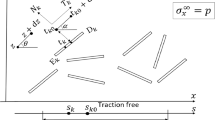
Singular integral equations have been applied to the quasistatic growth of an edge crack in an isotropic elastic half-plane when an arbitrary non-self-balancing load is applied to the edges, and in particular when one of the edges is subject to a localized force. The path has been constructed in a step fashion on the basis of the stress redistribution during crack growth. The singular integral equations are solved by mechanical quadrature.
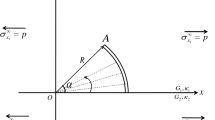
The paths and the stress intensity coefficients along them have been calculated for cases where one of the edges of a crack initially perpendicular to the boundary is, acted on by a constant normal pressure or normal localized force. The direction of the crack increment is derived from the criterion for maximal circumferential stresses.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
M. P. Savruk, P. N. Osiv, and I. V. Prokopchuk, Numerical Analysis in Planar Aspects of Cracking Theory [in Russian], Naukova Dumka, Kiev (1989).
S. Ya. Yarema, “Propagation of a curvilinear crack in a plate,” Izv. Akad. Nauk SSSR, Mekh. Tverd. Tela, No. 2, 156–163 (1988).
M. P. Savruk, Two-Dimensional Problems in Elasticity for a Body Containing Cracks [in Russian], Naukova Dumka, Kiev (1981).
M. P. Savruk and P. N. Osiv, “Calculation of the crack static propagation path,” Probl. Prochn., No. 11, 19–23 (1982).
A. P. Datsyshin, P. N. Osiv, and G. P. Marchenko, “Static crack growth paths in plates,” in: Abstracts for the 1st All-Union Conference on Failure Mechanics, L'vov, 20–22 October 1987 [in Russian], L'vov (1987), p. 115.
V. V. Panasyuk, A. I. Zboromirskii, G. S. Ivanitskaya, and S. Ya. Yarema, “Applicability of the 385-01 criterion for calculating crack paths,” Probl. Prochn., No. 9, 3–7(1986).
V. V. Panasyuk and L. T. Berezhnitskii, “Determining the limiting forces in the stretching of a plate containing a curved crack,” in: Aspects of the Mechanics of Real Solids [in Russian], Issue 3, Naukova Dumka, Kiev (1964), pp. 3–19.
A. P. Datsyshin and G. P. Marchenko, “Interaction of a curvilinear crack with the boundary of an elastic half-plane,” Fiz.-Khim. Mekh. Mater., No. 5, 64–71 (1984).
V. V. Panasyuk, M. P. Savruk, and A. P. Datsyshin, Stress Distribution around a Crack in a Plate or Shell [in Russian], Naukova Dumka, Kiev (1976).
F. D. Gakhov, Boundary-Value Problems [in Russian], Fizmatgiz, Moscow (1963).
M. M. Chawla and T. R. Ramakrishnan, “Modified Gauss-Jacobi quadrature formulas for the numerical evaluation of Cauchy-type singular integrals,” BIT (Sver.),14, No. 1, 14–21 (1974).
Author information
Authors and Affiliations
Additional information
Translated from Fiziko-Khimicheskaya Mekhanika Materialov, Vol. 27, No. 4, pp. 53–59, July–August, 1991.
Rights and permissions
About this article
Cite this article
Datsishin, O.P., Marchenko, G.P. Quasistatic edge crack growth with non-self-balancing stresses at the edges. Mater Sci 27, 379–385 (1992). https://doi.org/10.1007/BF00723229
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00723229