Skip to main content
SpringerLink
Log in

Fluctuations in dense gas concentrations measured in a wind-tunnel

  • Published:
Boundary-Layer Meteorology Aims and scope Submit manuscript

Abstract

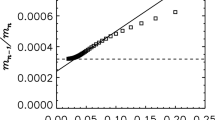
Concentration time series from FID (flame ionisation detector) sensors and catharometers downstream of an instantaneous release of dense gas contaminants are analysed by statistical methods. For each experiment there are either 50 or 100 replications, thus allowing estimates of statistical properties to be made even though the dispersion is nonstationary. The time history of the first four central moments is estimated, and they are plotted against each other, in the manner suggested by Mole and Clarke (1995). The collapse of the skewness-kurtosis plot onto a universal quadratic curve, similar to that found by Mole and Clarke for continuous releases, is observed. In this paper, we show how this observation is consistent with the form of the pdf postulated by Chatwin and Sullivan (1989).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Batchelor, G. K.: 1959, ‘Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity’,J. Fluid Mech. 5, 113–133.

    Google Scholar 

  • Carn, K. K. and Chatwin, P. C.: 1985, ‘Variability and heavy gas dispersion’,J. Haz. Mat. 11, 281–300.

    Google Scholar 

  • Chatwin, P. C.: 1980, ‘Presentation of longitudinal dispersion data’,J. Hydraulic Div. ASCE,106(HY1, 15150), 71–83.

    Google Scholar 

  • Chatwin, P. C.: 1982, ‘The use of statistics in describing and predicting the effects of dispersing gas clouds’,J. Haz. Mat. 6, 213–230.

    Google Scholar 

  • Chatwin, P. C. and Sullivan, P. J.: 1989, ‘The intermittency factor of scalars in turbulence’Phys. Fluids A,1 (4), 761–763.

    Google Scholar 

  • Chatwin, P. C. and Sullivan, P. J.: 1990, ‘A simple and unifying physical interpretation of scalar fluctuation measurements from many turbulent shear flows’,J. Fluid Mech. 212, 533–556.

    Google Scholar 

  • Chatwin, P. C., Lewis, D. M., and Mole, N.: 1994, ‘Practical statistical models of environmental pollution’,to appear in Mathematical and Computer Modeling.

  • Chatwin, P. C., Lewis, D. M., and Sullivan, P. J.: 1995, ‘Turbulent dispersion and the Beta distribution’,submitted to Environmetrics.

  • Fackrell, J. E. and Robins, A. G.: 1982, ‘Concentration fluctuations and fluxes in plumes from point sources in a turbulent boundary layer’,J. Fluid Mech. 117, 1–26.

    Google Scholar 

  • Hall, D. J., Waters, R. A., Marsland, G. W., Upton, S. L., and Emmott, M. A.: 1989, ‘Repeat variability in instantaneously released heavy gas clouds-some wind tunnel experiments’, Technical Report LR 804 (PA), Warren Spring Laboratory.

  • Mylne, K. R. and Mason, P. J.: 1981, ‘Concentration fluctuation measurements in a dispersing plume at a range of up to 1000m’,Quart. J. Roy. Meteorol. Soc.,117, 177–206.

    Google Scholar 

  • Mole, N. and Clarke, E. D.: 1995, ‘Relationships between the higher moments of concentration and of dose in turbulent dispersion’,Boundary-Layer Meteorol. in press.

  • McQuaid, J.: 1985, ‘Design of the Thorney Island continuous release trials’,J. Haz. Mat.,16, 1–8.

    Google Scholar 

  • Pasquill, F.: 1961, ‘The estimation of the dispersion of windborne material’, “Meteorol. Mag.”,90(1063), 33–49.

    Google Scholar 

  • Pope, S. B.: 1985, ‘Pdf methods for turbulent reactive flows’, “Prog. Energy Combust. Sci.”11, 119–192.

    Google Scholar 

  • Robinson, C.: 1995, ‘An overview of gas dispersion with fences’,School of Mathematics and Statistics, University of Sheffield report no. TR/01/95.

  • Sawford, B. L. and Sullivan, P. J.: 1995, ‘A simple representation of a developing contaminant concentration field’, “to appear in J. Fluid Mech.”.

  • Tennekes, H. and Lumley, J. L.: 1972, “A First Course in Turbulence”. MIT Press.

  • Weil, J.C., Sykes, R. I., and Venkatram, A.: 1992, ‘Evaluating air quality models: review and outlook’J. Appl. Meteorol. 31, 1121–1145.

    Google Scholar 

  • Zimmerman, W. B. and Chatwin, P. C.: 1995, ‘Statistical fluctuations due to microscale mixing in a diffusion layer’,Environmetrics 6 (6).

Download references

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, UMIST, PO Box 88, M60 1QD, Manchester, UK

    William B. Zimmerman

  2. Applied Mathematics Section, School of Mathematics and Statistics, University of Sheffield, S10 2UN, Sheffield, UK

    P. C. Chatwin

Authors
  1. William B. Zimmerman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. C. Chatwin
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zimmerman, W.B., Chatwin, P.C. Fluctuations in dense gas concentrations measured in a wind-tunnel. Boundary-Layer Meteorol 75, 321–352 (1995). https://doi.org/10.1007/BF00712268

Download citation

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00712268

Keywords

Search

Navigation