Skip to main content
SpringerLink
Log in

The integrable cases of the planetary three-body problem at first-order resonance

  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

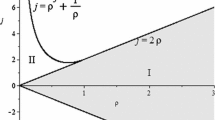
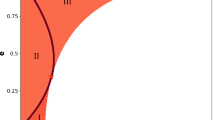
This paper investigates the stability of the motion in the averaged planar general three-body problem in the case of first-order resonance. The equations of the averaged motion of bodies near the resonance surface is obtained and is analytically integrated by quadratures. The stability of the averaged motion is analytically investigated in relation to the semi-major axes, the eccentricities and the resonance phases. An autonomous second-order equation is obtained for the deviation of semiaxes from the resonance surface. This equation has an energy integral and is analytically integrated by quadratures. The quasi-periodic dependence on time with two-frequency basis of the averaged motion of bodies is found. The basic frequencies are analytically calculated. With the help of the mean functionals calculated along integral curves of the averaged problem the new analytic first integrals are constructed with coefficients periodic in time. The analytic conditions of librations of resonance phases are obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ferraz-Mello, S. and Sessin, W.: 1984,Celest. Mech. 34, 453.

    Google Scholar 

  2. Ferraz-Mello, S.: 1987,Publ. Astron. Inst. Czech. Acad. Sci. 68, 49.

    Google Scholar 

  3. Ferraz-Mello, S.: 1987,Astron. J. 94, 208.

    Google Scholar 

  4. Ferraz-Mello, S.: 1988,Astron. J. 96, 400.

    Google Scholar 

  5. Froeschle, C.: 1984,Celest. Mech. 40, 95.

    Google Scholar 

  6. Froeschle, C. and Scholl, H.: 1985,Astron. Astrophys. 42, 457.

    Google Scholar 

  7. Henrard, J. and Lemaître, A.: 1986,Celest. Mech. 39, 213.

    Google Scholar 

  8. Henrard, J. and Lemaître, A.: 1987,Icarus 69, 266.

    Google Scholar 

  9. Hori, G.-I.: 1966,Publ. Astron. Soc. Jpn. 18, 287.

    Google Scholar 

  10. Hills, J.G.: 1970,Nature 225, 840.

    Google Scholar 

  11. Kozai, Y.: 1985,Celest. Mech. 36, 48.

    Google Scholar 

  12. Murray, C.D.: 1985,Icarus 65, 70.

    Google Scholar 

  13. Ovenden, M.W., Feadgin, T. and Graff, O.: 1974,Celest. Mech. 8, 455.

    Google Scholar 

  14. Ovenden, M.W. and Roy, A.E.: 1954,M.W. Mon. Not. Roy. Astron. Soc. 114, 232.

    Google Scholar 

  15. Roy, A.: 1982,Orbital Motion, Adam Hilger, 2nd ed.

  16. Salgado, T.M.V. and Sessin, W.: 1985, in S. Ferraz-Mello and W. Sessin (eds.),The Motion of Planets and Natural and Artificial Satellites, Univ. São Paulo, p. 93.

  17. Sessin, W.: 1981, Dr. thesis (Univ. São Paulo).

  18. Sessin, W.: 1983,Celest. Mech. 29, 361.

    Google Scholar 

  19. Sessin, W. and Ferraz-Mello, S.: 1984,Celest. Mech. 32, 307.

    Google Scholar 

  20. Shinkin, V.N.: 1981,Vestnik Moskov, Gosud. Univ. Serija 15,2, 22.

    Google Scholar 

  21. Wisdom, J.: 1987,Icarus 72, 241.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Scientific and Organizational Management Department, Russian Academy of Sciences, Moscow, Russia

    V. N. Shinkin

Authors
  1. V. N. Shinkin
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shinkin, V.N. The integrable cases of the planetary three-body problem at first-order resonance. Celestial Mech Dyn Astr 55, 249–259 (1993). https://doi.org/10.1007/BF00692513

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00692513

Key words

Search

Navigation