Skip to main content
SpringerLink
Log in

Spherical shock waves in viscous magnetogasdynamics

  • Published:
Astrophysics and Space Science Aims and scope Submit manuscript

Abstract

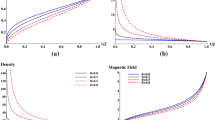
The point-source, spherical magnetogasdynamics shock wave moving into a constant density γ-law gas is considered in the limit of infinite shock strength, from the point of view of the Richtmyer-Von Neumann viscosity technique. Numerical solutions of this problem has been obtained in viscous and non-viscous regions. A similarity solution of this problem is shown to exist. We have shown that field variables change rapidly when the magnetic field is imposed in both the viscous and the non-viscous regions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  • Brode, H. L.: 1954, Rand Corporation Report to the Atomic Energy Commission, p. 571.

  • Christy, R. F.: 1964,Rev. Mod. Phys. 36, 555.

    Google Scholar 

  • Colgate, S. A. and Johnson, M. H.: 1960,Phys. Rev. Letters 5, 235.

    Google Scholar 

  • Latter: 1955,Journal of Applied Physics 26(8), 954.

    Google Scholar 

  • Lax, P. D.: 1954,Comm. Pure Applied Math. 7, 159.

    Google Scholar 

  • Richtmyer, R. D. and Von Neumann, J.: 1950,J. Appl. Phys. 21, 232.

    Google Scholar 

  • Sachdev, P. L. and Prasal Phoolan: 1966,J. Phys. Soc. Japan 21, 12.

    Google Scholar 

  • Summers, D.: 1975,Astron. Astrophys. 45, 151.

    Google Scholar 

  • Taylor: 1950,Proc. Roy. Soc. (London) A201, 159.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Gorakhpur, U. P., India

    B. G. Verma, R. C. Srivastava & V. K. Singh

Authors
  1. B. G. Verma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. C. Srivastava
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. K. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Supported by CSIR, New DeIhi under the grant No. 7157/287/81-DMR-I.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Verma, B.G., Srivastava, R.C. & Singh, V.K. Spherical shock waves in viscous magnetogasdynamics. Astrophys Space Sci 111, 253–263 (1985). https://doi.org/10.1007/BF00649969

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00649969

Keywords

Search

Navigation