Abstract
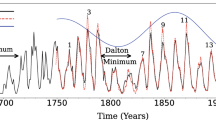
Recently, the origin of the solar cycle is considered to be rooted in the dynamics of the solar core (Grandpierre, 1996). The dynamic solar core model requires macroscopic flow and magnetic field as basic inputs. The macroscopic flow cannot be generated by the quasistatic solar structure and it has to reach a larger than critical size (Grandpierre, 1984) in order to survive dissipation. Therefore the flow must be generated by outer agents. The most significant outer agents to the Sun are the planets of the Solar System. These theoretical arguments are supported by observations showing that planetary tides follow a pattern correlating with the solar cycle in the last three and a half centuries (Wood, 1972; Desmoulins, 1995). Therefore the pulsating-ejecting solar core model gives a firm theoretical basis for the interpretation of these largely ignored observations. In this paper a new and simple calculation is presented which enlightens the planetary origin of the eleven-year period and gives a physical basis for a detailed modelling of the dynamo and the solar cycle.
Similar content being viewed by others
References
Babcock, H.W.: 1961,Astrophys. J. 133, 572.
Currie, R.G.: 1973,Astrophys. Space Sci. 20, 509.
Desmoulins, J.-P. 1995,http://www.alpes — net. fr/~j_p_desm/sunspots.html.
Dobrolyubov, A.I.: 1991,Appl. Mech. Rev. 44, 215.
Dobrolyubov, A.I.: 1993, in: ‘Moon and Living Matter’, International Workshop, Kosice, Slovakia, September 23–25, 1993, Program and Abstracts, 19.
Dodson, H.W. and Hedeman, E.R.: 1972, in: P.S. McIntosh and M. Dryer (eds.),Solar Activity Observations and Predictions, Boulder, NAO, 19.
Dziembowski, W.A. and Goode, P.R.: 1993, in: T.M. Brown (ed.),GONG 1992: Seismic Investigations of the Sun and Stars, 225.
Edmonds, F.B.: 1882,Nature 26, 292.
Grandpierre, A.: 1984, in: A. Noels and M. Gabriel (eds.),Theoretical Problems in Stellar Stability and Oscillations, 48.
Grandpierre, A.: 1990,Sol. Phys. 128, 3.
Grandpierre, A.: 1996,Astron. Astrophys. 308, 119.
Gribbin, J. and Plagemann, S.: 1977,Jupiter Effect Revisited, Fontana, Collins.
Hantzsche, E.: 1978,Astron. Nachr. 299, 259.
Novotny, O.: 1983, in: A.M. Soward (ed.),Stellar and Planetary Magnetism, Gordon and Breach, New York, 289.
Okal, E. and Anderson, D.L.: 1975,Nature 253, 511.
Olah, K., Hall, D.S. and Henry, G.W.: 1991,Astron. Astrophys. 251, 531.
Opik, E.: 1972,Irish Astron. J. 10, 298.
Phillips, K.J.H.: 1992,Guide to the Sun, Cambridge Univ. Press, 70.
Seymour, P.A.H., Willmott, M. and Turner, A.: 1992,Vistas in Astron. 35, 39.
Verma, S.D.: 1986, in: K.B. Bhatnagar (ed.),Space Dynamics and Celestial Mechanics, D. Reidel,Astrophys. Space Sci. Libr. 127, 143.
Wood, K.D.: 1972,Nature 240, 91.
Wood, R.M.: 1975,Nature 255, 312.
Zeilik, M., De Blasi, C., Rhodes, M. and Budding, E.: 1988,Astrophys. J. 332, 293.
Zeilik, M., Cox, D.A., De Blasi, C., Rhodes, M. and Budding, E.: 1989,Astrophys. J. 345, 991.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Grandpierre, A. On the origin of solar cycle periodicity. Astrophys Space Sci 243, 393–400 (1996). https://doi.org/10.1007/BF00644709
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00644709