Electron transport in corona charged 12 μm teflon FEP with saturable deep traps

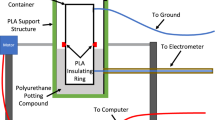
Abstract

Surface-potential measurements carried out in negatively corona charged 12 μm samples of fluorethylenepropylene (Teflon FEP) showed the following characteristics: 1) with a constant charging current, the potential initially rises linearly, and then sublinearly; 2) the potential saturates irrespectively of the charging process and 3) practically no potential decay is observed after switching off the corona. These results have been interpreted in terms of an usual model (field-independent trapping time) for charge transport in insulators, with saturable deep traps in both surface and bulk of the sample and a relatively high electron mobility in order to prevent free-space charge accumulation. The partial differential equations derived from the model are numerically solved and it was found that only the product of the mobility μ with the trapping time is relevant to the fitting of experimental results, provided that μ>10⁻⁸ cm²/Vs. A field-dependent trapping time model leads to poorer fittings.