Abstract
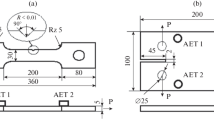
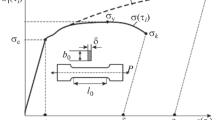
The identification of crack growth signals is extremely important in order to effectively use acoustic emission techniques to detect, locate, and determine the significance of an internal flaw. The results of an analytical methodology, incorporating a source model that is an actual crack propagation and arrest event, are presented in this paper to predict a time dependent acoustic emission signal. The integral equation method is used to calculate the dynamic Mode I stress caused by a crack propagating with a prescribed velocity, after which the displacements at any point are calculated. These time dependent displacements are the analytical form of the acoustic emission waveforms. An experimental procedure, which uses a laser interferometer to measure velocities normal to the specimen's surface, is used to investigate acoustic emission waveforms in a compact tension specimen. The experimental results are used to verify the analytical model.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
L. B. Freund, The initial wave front emitted by a suddenly extending crack in an elastic solid,J. Appl. Mech. 39601–602 (1972).
L. R. F. Rose, The stress-wave radiation from a growing crack,Int. J. Fract. 1745–60 (1981).
J. D. Achenbach and J. G. Harris, Acoustic emission from a brief crack growth event,J. Appl. Mech. 46107–112 (1979).
D. G. Eitzen and H. N. G. Wadley, Acoustic emission: Establishing the fundamentals,J. Res. National Bureau Standards 8975–100 (1984).
Y. H. Pao, Theory of acoustic emission,Elastic Waves and Non-destructive Testing of Materials (ASME AMD-29, 1978), pp. 107–128.
A. N. Ceranoglu and Y. H. Pao, Propagation of elastic pulses and acoustic emission in a plate, Part 1: Theory,J. Appl. Mech. 48125–132 (1981).
A. N. Ceranoglu and Y. H. Pao, Propagation of elastic pulses and acoustic emission in a plate, Part 2: Epicentral responses,J. Appl. Mech. 48133–138 (1981).
A. N. Ceranoglu and Y. H. Pao, Propagation of elastic pulses and acoustic emission in a plate, Part 3: General responses,J. Appl. Mech. 48139–147 (1981).
K. Y. Kim and W. Sachse, Acoustic emission from penny-shaped cracks in glass. I. Radiation pattern and crack orientation,J. Appl. Phys. 592704–2710 (1986).
K. Y. Kim and W. Sachse, Acoustic emission from penny-shaped cracks in glass. II. Moment tensor and source-time function.J. Appl. Phys. 592711–2715 (1986).
K. Y. Kim and W. Sachse, Characteristics of an acoustic emission source from a thermal crack in glass,Int. J. Fract. 31211–231 (1986).
M. Ohtsu and K. Ono, The generalized theory and source representations of acoustic emission,J. Acoust. Emission 5124–133 (1986).
M. Ohtsu, Source kinematics of acoustic emission based on a moment tensor,NDT Int. 2214–20 (1989).
M. Enoki and T. Kishi, Theory and analysis of deformation moment tensor due to microcracking,Int. J. Fract. 38295–310 (1989).
L. J. Jacobs and M. P. Bieniek, An integral equation method for dynamic crack growth problems,Int. J. Fract. 46207–221 (1990).
L. J. Jacobs, Characterization of acoustic emission signals from a mode I crack,J. Eng. Mech. 1171878–1889 (1991).
J. D. Achenbach,Wave Propagation in Elastic Solids (North-Holland, 1973).
R. Weiss and R. S. Anderssen, A product integration method for a class of singular first kind Volterra equations,Numerishe Mathematik 18442–456 (1972).
P. J. Davis and P. Rabinowitz,Methods of Numerical Integration (Academic Press, 1984).
S. Huber, W. R. Scott, and R. Sands, Detection of ultrasonic waves propagating in boron/aluminum and steel/lucite composite materials,Rev. Prog. Quant. Nondestr. Eval. 6B1065–1074 (1987).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Jacobs, L.J., Scott, W.R., Granata, D.M. et al. Experimental and analytical characterization of acoustic emission signals. J Nondestruct Eval 10, 63–70 (1991). https://doi.org/10.1007/BF00568101
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00568101