Abstract
The pressure field on the ground plane around three-dimensional bluff bodies with varying relative dimensions has been obtained experimentally. The pressure measurements along the plane of symmetry are presented for the cases when the bodies are exposed to a uniform approach flow (without the presence of a horse-shoe vortex) and when the bodies are kept in a boundary layer. The results show extreme base suction for a body with a relative length to width ratio (l/b) of 0.5. A horse-shoe vortex exists at the front end for the bodies kept in the boundary layer. The isobaric coefficient contours presented for the region away from the plane of symmetry clearly indicate the regions of suction pressure around the bodies and how they vary with the relative dimensions. The vortex system at the front end is also revealed by the isobars.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Abbreviations
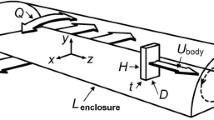
- b :
-
width of the body
- C PW :
-
(p−p r)/1/2ρU 2r , pressure coefficient on the ground
- h :
-
height of the body
- l :
-
length of the body along the flow direction
- p :
-
pressure at any point on the surface plate with the body
- p r :
-
pressure at the same point on surface plate without the body
- U r :
-
free stream reference velocity
- x :
-
coordinate along the flow direction
- x r :
-
reattachment distance
- z :
-
coordinate normal to x and in the plane of the ground
- δ :
-
boundary layer thickness
- δ*:
-
displacement boundary layer thickness
- (-):
-
( )/b
References
H.J. Leutheusser and W.D. Baines, Similitude problems in building aerodynamics, ASCE J. Hydraulic Div. HY3 93 (1967) 35.
V.Kr. Sharan, On characteristics of flow around building models with the view of simulating the minimum fraction of the boundary layer, Internat. J. Mech. Sci. 17 (1975) 557.
W.J. Beranek, General rules for the determination of wind environment. Proc. 5th Internat. Conf. on Wind Engrg, Fort Collins, Colorado, USA (1979).
I.P. Castro and A.G. Robins, The flow around a surface mounted cube in uniform and turbulent streams, J. Fluid Mech. 79 (1977) 307.
Y. Ogawa and S. Oikawa, A field investigation of the flow and diffusion around a model cube. Atmospheric Environment 16 (1982) 207.
H. Sakamoto and M. Arie, Flow around a cubic body immersed in a turbulent boundary layer, J. Wind Engrg. and Industrial Aerodynamics 9 (1982) 275.
J.C.R. Hunt, C.J. Abell, J.A. Peterka and H. Woo, Kinematical studies of the flow around free and surface mounted obstacles applying topology to flow visualization, J. Fluid Mech. 86 (1978) 179.
B.H.L. Gowda, H.J. Gerhardt and C. Kramer, Surface flow field around three-dimensional bluff bodies, Proc. 5th Colloquium on Industrial Aerodynamics, Fachhochschule Aachen, FRG, Part 2 (1982) 121.
L. Belik, The secondary flow about circular cylinders mounted normal to a flat plate, Aeron. Quart. 24 (1973) 47.
C.J. Baker, The turbulent horse-shoe vortex. J. Wind Engrg. and Industrial Aerodynamics 6 (1980) 9.
H. Nakaguchi, Recent research on three-dimensional bluff body flows related to road vehicle aerodynamics, in; G. Sovran, T. Morel and W.T. Mason (eds.) Aerodynamic drag of bluff bodies and road vehicles, Plenum Press, new York (1978) 227.
F. Etzold and H. Fiedler, The near-wake structure of a cantilevered cylinder in a cross-flow, Z. für Flugwissenschaften 24 (1976) 77.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Gowda, B.H.L., Gerhardt, H.J. & Kramer, C. Pressure field around three-dimensional bluff bodies. Appl. Sci. Res. 42, 245–263 (1985). https://doi.org/10.1007/BF00539343
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00539343