Skip to main content
SpringerLink
Log in

Slip flow in the hydrodynamic entrance region of a tube and a parallel plate channel

  • Published:
Applied Scientific Research, Section A Aims and scope Submit manuscript

Summary

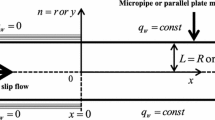
The problem of slip flow in the entrance region of a tube and parallel plate channel is considered by solving a linearized momentum equation. The condition is imposed that the pressure drop from momentum considerations and from mechanical energy considerations should be equal. Results are obtained for Kn=0, 0.01, 0.03, 0.05, and 0.1 and the pressure drop in the entrance region is given in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

cross-sectional area of duct

c :

mean value of random molecular speed

d :

diameter of tube

f p :

\({{h \cdot \frac{{dp}}{{dx}}} \mathord{\left/ {\vphantom {{h \cdot \frac{{dp}}{{dx}}} {\tfrac{1}{2}\rho u^2 }}} \right. \kern-\nulldelimiterspace} {\tfrac{1}{2}\rho u^2 }}\)

f t :

\({{\tfrac{1}{2}r_{\text{t}} \frac{{dp}}{{dx}}} \mathord{\left/ {\vphantom {{\tfrac{1}{2}r_{\text{t}} \frac{{dp}}{{dx}}} {\tfrac{1}{2}\rho u^2 }}} \right. \kern-\nulldelimiterspace} {\tfrac{1}{2}\rho u^2 }}\)

h :

half height of parallel plate channel

Kn :

Knudsen number

L :

molecular mean free path

n :

directional normal of solid boundary

p :

pressure

p 0 :

pressure at inlet

r :

radial co-ordinate

r t :

radius of tube

R :

non-dimensional radial co-ordinate

Re p :

4hU/ν

Re t :

2r t U/ν

s :

direction along solid boundary

T :

absolute temperature

u :

velocity in x direction

u*:

non-dimensional velocity

U :

bulk velocity = (1/A) ∫ A u dA

v :

velocity in y direction

x :

axial co-ordinate

x*:

stretched axial co-ordinate

X :

non-dimensional axial co-ordinate

X*:

non-dimensional stretched axial co-ordinate

Y :

non-dimensional channel co-ordinate

α :

eigenvalue in parallel plate channel

ε :

stretching factor

λ :

eigenvalue in tube

ρ :

density

ν :

kinematic viscosity

i :

index

p :

parallel plate

t :

tube

v :

velocity vector

∇ :

gradient operator

∇ 2 :

Laplacian operator

References

  1. Sparrow, E. M., T. S. Lundgren and S. H. Lin, Slip flow in the entrance region of a parallel plate channel. Proceedings of 1962 Heat Transfer and Fluid Mechanics Institute, Stanford Pg. 233.

  2. Siezkin, N. A., Dynamics of Viscous incompressible fluids, Moscow Gostekhizdat. 1955.

  3. Hanks, R. W., Phys. Fluids 6 (1963) 1645.

    Google Scholar 

  4. Sparrow, E. M. and S. H. Lin, Phys. Fluids 7 (1964) 338.

    Google Scholar 

  5. Patterson, G. N., Molecular flow of gases. Wiley, New York, 1956.

    Google Scholar 

  6. Kennard, E. H., Kinetic theory of gases. McGraw Hill, New York, 1938.

    Google Scholar 

  7. Lundgren, T. S., E. M. Sparrow and J. B. Starr, J. Basic Engg. 86 Series D (1964) 620.

    Google Scholar 

  8. Langhaar, H. L., J. Appl. Mech. 9 (1942) 55.

    Google Scholar 

  9. Dong, W. and L. A. Bromley, Vacuum flow of gases through channels with circular annular and rectangular cross-section. Trans 8th Vacuum Symp. Washington, Pergamon 1962.

Download references

Author information

Authors and Affiliations

  1. Faculty of Technology, University of Manchester, England

    Alan Quarmby

Authors
  1. Alan Quarmby
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Quarmby, A. Slip flow in the hydrodynamic entrance region of a tube and a parallel plate channel. Appl. sci. Res. 15, 411–428 (1966). https://doi.org/10.1007/BF00411575

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00411575

Keywords

Search

Navigation