Skip to main content
SpringerLink
Log in

Transient heat transfer in the laminar thermal entry region of a pipe: an analytical solution

  • Published:
Applied Scientific Research Aims and scope Submit manuscript

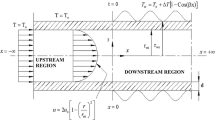
Abstract

Attention is directed toward the problem of unsteady convective heat transfer to a fluid flowing inside a pipe in a laminar, fully developed fashion when suddenly, an ambient fluid outside the pipe undergoes a step change in temperature. For the fastest portion of the resultant transient, time domain I, an analytical solution of the governing partial differential thermal energy equation is effected via the Laplace transformation. From this solution, response functions are found for the pipe wall temperature, surface heat flux, and fluid bulk mean temperature as a function of non-dimensional time for a range of values of a parameter which characterizes the heat transfer between the ambient and the pipe.

Comparison of results is made with a recent finite difference solution in the literature and with the standard quasi-steady type of analysis. It is found that the analytical solution presented herein extends and complements the finite difference solution and that the quasi-steady solution can be severely in error in this part of the transient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

â :

ρc p R/ρwcpwb Ratio of thermal energy storage capacity of fluid to wall material

b :

pipe wall thickness

C n :

defined by equation (24)

c p , c pw :

specific heat capacity of fluid and pipe wall, respectively

D n :

functions defined by equation (23)

erf, erfc:

error function and complimentary error function, respectively

F :

αt/R 2 Fourier number

g :

1−2S

h :

local surface coefficient of heat transfer between inside of pipe wall and inside flowing fluid

i n erfc:

n th repeated integral of the error function

k :

thermal conductivity of the inside fluid

N :

h(2R)/k Nusselt number

p :

Laplace transform parameter

q w :

local, instantaneous surface heat flux at inside of pipe wall

Q w :

2Rq w /k(T L −T i ) nondimensional surface heat flux

R :

pipe inside radius

S :

UR/k

t :

time

T :

local instantaneous fluid temperature

T B , T L , T i :

bulk mean, ambient, and initial, as well as inlet, temperature, respectively

u, u m :

local and mass average, fluid velocity, respectively

U :

overall heat transmission coefficient between ambient fluid outside of pipe and inside pipe wall

X, Y :

x/R, y/R nondimensional space coordinates along, and radially inward from, the pipe wall, respectively

α :

k/ρc p thermal diffusivity of inside fluid

ρ, ρ w :

mass density of inside fluid and wall, respectively

φ :

(T(x, y, t)−T i )/(T L −T i )

φ w , φ B :

wall, bulk mean value of φ, respectively

References

  1. J. Sucec, An improved quasi-steady approach for transient conjugated forced convection problems, Int. J. Heat Mass Transfer 24 (1981) 1711–1722.

    Google Scholar 

  2. J.A. Clark, V.S. Arpaci, and K.M. Treadwell, Dynamic response of heat exchangers having internal heat sources — Part I, Trans. A.S.M.E. 80 (1958) 612–624.

    Google Scholar 

  3. R. Siegel, Heat transfer for laminar flow in ducts with arbitrary time variations in wall temperature, J. Applied Mech. 27 (1960) 241–249.

    Google Scholar 

  4. D.G. Drake Unsteady conjugated heat transfer near a stagnation point, Appl. Sci. Res. 40 (1983) 199–207.

    Google Scholar 

  5. B. Krishan, On conjugated heat transfer in fully developed flow, Int. J. Heat Mass Transfer 25 (1982) 288–291.

    Google Scholar 

  6. T.F. Lin, K.H. Hawkes, and W. Leidenfrost, Unsteady thermal entrance heat transfer in laminar pipe flows with step change in ambient temperature, Warme-Stoffubertrag 17 (1983) 125–132.

    Google Scholar 

  7. M.J. Lighthill, Contributions to the theory of heat transfer through laminar boundary layer, Proc. R. Soc. Lond. (Ser. A), London (1966) 349–351.

  8. G.E. Roberts and H. Kaufmann, Tables of Laplace Transforms, W.B. Saunder Co., Philadelphia, Pa. (1966).

    Google Scholar 

  9. M. Abramowitz and I. Stegun (eds.), Handbook of Mathematical Functions, Dover, New York (1965).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Maine, Room 219 Boardman Hall, 04 469, Orono, ME, USA

    James Sucec (Professor of Mechanical Engineering)

Authors
  1. James Sucec
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sucec, J. Transient heat transfer in the laminar thermal entry region of a pipe: an analytical solution. Appl. Sci. Res. 43, 115–125 (1986). https://doi.org/10.1007/BF00386039

Download citation

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00386039

Keywords

Search

Navigation