Numerical analysis of viscoplastic axisymmetric shells based on a hybrid strain finite element

Abstract

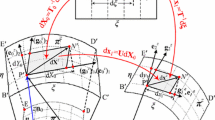
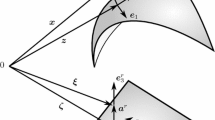
The viscoplastic deformation behavior of the shell is governed by any of the more recently proposed unified constitutive models with internal state variables and with the assumption that the total strain rate tensor can be decomposed additively into an elastic and an inelastic part. For the numerical analysis of viscoplastically deformed shells we use a hybrid strain finite element based on a geometrically linear theory of inelastic shells proposed by Kollmann and Mukherjee (1985). This theory gives the reduction of a two-field variational principle originally proposed by Oden and Reddy (1974) for elastic shells to the shell midsurface. It contains strain and displacement rates as variables to be independently varied. The shell formulation of this variational principle is the basis for the present work. First, a general hybrid finite element model is derived in which the shape functions for the strain and displacement rates can be polynomials of different order. Here we use the term “hybrid” in the sense of Pian (1988), i.e. in our two-field finite element the strain rates are condensed statically on the element level, leaving nodal displacements as the only unknowns in the final matrix equation. Then the finite element model is specialized for an axisymmetrically loaded conical shell with linear approximation of the strain rate field and quadratic interpolation of the displacement rates. Special emphasis is given to the derivation of the inelastic pseudo-forces and pseudo-moments. Numerical results for elastically and viscoplastically deformed shells are presented, where viscoplastic deformations are described by Hart's (1976) constitutive model.