Skip to main content
SpringerLink
Log in

Green's function method for axisymmetric flows: analysis of the Taylor-Couette flow

  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

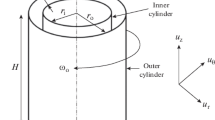
A numerical method for the solution of the Navier-Stokes equations in rotationally symmetric flow problems is presented. The numerical procedure is based on a boundary integral equation formulation with the fundamental solution of the Stokes' equation accounting for the rotational symmetry. The proposed methodology has been applied to the study of the Taylor-Couette flow between two concentric rotating cylinders of infinite axial length. A comparison with the available theoretical, experimental or numerical findings is performed to evaluate the accuracy of the present results. As predicted by the analytical theory and confirmed by the experiments, multiple solutions that are found for Reynolds numbers higher than the critical value, indicate the proposed methodology as a useful tool to get physical insight on the instabilities occurring in the solution of the Navier-Stokes equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Alonso, C. V.; Macagno, E. O. (1973): Numerical integration of the time-dependent equations of motion for Taylor vortex flow. Comput. Fluids 1, 301–316

    Google Scholar 

  • Burkhalter, J. E.; Koschmieder, E. L. (1974): Steady supercritical Taylor vortices after sudden starts. Phys. Fluids 17, 1929–1935

    Google Scholar 

  • Chandrasekhar, S. (1961): Hydrodynamic and hydromagnetic stability. London: Oxford University Press

    Google Scholar 

  • Cliffe, K. A. (1988). Numerical calculation of the primary flow exchange process in the Taylor problem. J. Fluid Mech. 197, 57–79

    Google Scholar 

  • Coles, D. (1965): Transition in circular Couette flow. J. Fluid Mech. 21, 385–425

    Google Scholar 

  • Davey, A. (1962): The growth of Taylor vortices in flow between rotating cylinders. J. Fluid Mech. 14, 336–368

    Google Scholar 

  • DiPrima, R. C.; Eagles, P. M. (1977): Amplification rates and torques for Taylor vortex flow between rotating cylinders. Phys. Fluids. 20, 171–175

    Google Scholar 

  • DiPrima, R. C.; Swinney, H. L. (1981): Instabilities and transition in flow between rotating cylinders. In: Swinney, H. L.; Gollub, J. P. (eds): Hydrodynamic instability and the transition to turbulence. Berlin, Heidelberg, New York: Springer (Topics in applied physics vol. 45)

    Google Scholar 

  • Donnelly, R. J.; Simon, N. J. (1960): An empirical torque relation for supercritical flow between rotating cylinders. J. Fluid Mech. 7, 401–418

    Google Scholar 

  • Graziani, G. (1989): A boundary integral equation method for axisymmetric viscous flows. Int. J. Eng. Sci. 27, 855–864

    Google Scholar 

  • Graziani, G.; Piva, R.; Rajagopal, K. R. (1988): A boundary integral method for the rod-climbing problem. In: Achutan, P.; Majhi, S. N. (eds); Ist Int. Conf. Mathem. Modelling Sci. Technol., Madras, India. Delhi: Tata-McGraw-Hill

    Google Scholar 

  • Kogelman, S.; DiPrima, R. C. (1970): Stability of spatially periodic supercritical flows in hydrodynamics. Phys. Fluids 13, 1–11

    Google Scholar 

  • Ma, S. Y.; Graziani, G.; Piva, R. (1984): A boundary integral equation method for free surface viscous flows. Meccanica 19, 294–299

    Google Scholar 

  • Marcus, P. S. (1984): Simulation of Taylor-Couette flow. Part 1. Numerical methods and comparison with experiment. J. Fluid Mech. 146, 45–46

    Google Scholar 

  • Meyer, K. A. (1966): A two-dimensional time-dependent numerical study of rotational Couette flow. Ph.D. Dissertation, Stanford University, USA

  • Meyer-Spasche, R.; Keller, H. B. (1980): Computations of the axisymmetric flow between rotating cylinders. J. Comput. Phys. 35, 100–109

    Google Scholar 

  • Moser, R. D.; Moin, P.; Leonard, A. (1983): A spectral numerical method for the Navier-Stokes equations with applications to Taylor-Couette flow. J. Comput. Phys. 52, 524–544

    Google Scholar 

  • Piva, R.; Morino, L. (1987): Vector Green's function method for unsteady Navier-Stokes equations. Meccanica 22, 76–85

    Google Scholar 

  • Segel, L. A. (1962): The non-linear interaction of two disturbances in the thermal convection problem. J. Fluid Mech. 14, 97–114

    Google Scholar 

  • Serrin, J. (1959): On the stability of viscous fluid motions. Arch. Ration. Mech. Anal. 3, 1

    Google Scholar 

  • Snyder, H. A. (1969): Wavenumber selection at finite amplitude in rotating Couette flow. J. Fluid. Mech. 35, 273–298

    Google Scholar 

  • Stuart, J. T. (1958): On the non linear mechanics of hydrodynamic stability. J. Fluid Mech. 4, 1–21

    Google Scholar 

  • Taylor, G. I. (1923): Stability of viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. London Ser. A 23, 289–343

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Meccanica e Aeronautica, Università di Roma “La Sapienza”, Via Eudossiana, 18-00184, Roma, Italy

    G. Graziani

Authors
  1. G. Graziani
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by S. N. Atluri, December 8, 1989

Rights and permissions

Reprints and permissions

About this article

Cite this article

Graziani, G. Green's function method for axisymmetric flows: analysis of the Taylor-Couette flow. Computational Mechanics 7, 77–88 (1990). https://doi.org/10.1007/BF00375923

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00375923

Keywords

Search

Navigation