Skip to main content
SpringerLink
Log in

A boundary element alternating method for two-dimensional mixed-mode fracture problems

  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

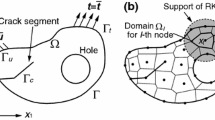
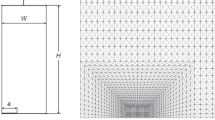
A boundary element alternating method (BEAM) is presented for two dimensional fracture problems. An analytical solution for arbitrary polynomial normal and tangential pressure distributions applied to the crack faces of an embedded crack in an infinite plate is used as the fundamental solution in the alternating method. For the numerical part of the method the boundary element method is used. For problems of edge cracks a technique of utilizing “finite elements” with BEAM is presented to overcome the inherent singularity in boundary element stress calculation near the boundaries. Several computational aspects that make the algorithm efficient are presented. Finally the BEAM is applied to a variety of two-dimensional crack problems with different configurations and loadings to assess the validity of the method. The method gave accurate stress-intensity factors with minimal computing effort.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Atluri, S. N.: Nishioka, T. (1986): Computational methods for three dimensional problems of fracture. In: Atluri, S. N. (ed): Computational methods in mechanics of fracture. North Holland, 230–287

  • Brebbia, C. A.; Dominguez, J. (1989): Boundary Elements — An Introductory Course. New York: Computational Mechanics Publications and McGraw-Hill

    Google Scholar 

  • Chen, K. L.; Atluri, S. N. (1988): A finite-element alternating method for cost-effective determination of weight-function and S.I.F.'s for multiple cracks in mixed-mode fracture. In: Atluri, S. N.; Yagawa, G. (eds). Computational Mechanics '88, Theory and Applications. Vol. 1, pp. 11.ii.1–11.ii.6. Berlin, Heidelberg, New York: Springer

    Google Scholar 

  • Hinton, E.; Campbell, J. S. (1974): Local and global smoothing of discontinuous finite-element functions using least squares method. Int. J. Num. Meth. Eng. 8, 461–480

    Google Scholar 

  • Hinton, E.; Campbell, J. S. (1975): Local least square stress smoothing for parabolic isoparametric elements. Int. J. Num. Meth. Eng. 9, 235–256

    Google Scholar 

  • Kantorovich, L. V.; Krylov, V. I. (1964): Approximate methods of higher analysis. New York: Interscience

    Google Scholar 

  • Krishnamurthy, T.; Raju, I. S. (1990): A finite-element alternating method for two-dimensional mixed-mode crack configurations. Eng. Fract. Mech. 36, 297–311

    Google Scholar 

  • Murakami, Y. et al. (eds) (1987): Stress intensity factors handbook Vols. 1 and 2. New York: Pergamon Press

    Google Scholar 

  • Nishioka, T.; Atluri, S. N. (1983a): Analytical solution for embedded elliptical cracks and finite element-alternating method for elliptical surface cracks, subjected to arbitrary loadings. Eng. Fract. Mech. 17, 247–268

    Google Scholar 

  • Nishioka, T.; Atluri, S. N. (1983b): An alternating method for analysis of surface flawed aircraft structural components. AIAA 21, 749–757

    Google Scholar 

  • Rajiyah, H.; Atluri, S. N. (1988): Evaluation of K-factors and weight functions for 2-D mixed mode multiple cracks by the boundary element alternating method. In: Altluri, S. N.; Yagawa, G. (eds): Computational Mechanics '88, Theory and Applications. Vol. 1, pp. 11.i.1–11.i.5, Berlin, Heidelberg, New York: Springer

    Google Scholar 

  • Raju, I. S.; Atluri, S. N.; Newman, J. C., Jr. (1987): Stress-intensity factors for small surface and corner cracks in plates. Paper Presented at the 20th National Symposium on Fracture Mechanics, Lehigh University, Bethlehem, Pa, 23–25

  • Raju, I. S.; Fichter, W. B. (1989): A finite-element alternating method for two dimensional mode I crack configurations. Eng. Fract. Mech. 33, 525–540

    Google Scholar 

  • Rooke, D. P.; Cartwright, D. J. (1976): Compendium of stress intensity factors. Uxbridge, Middlesex: The Hillingdon Press

    Google Scholar 

  • Sih, G. C. (1973): Handbook of stress intensity factors, Vols. 1 and 2, Lehigh University, Bethelhem, Pa.

    Google Scholar 

  • Tada, H.; Paris, P. C.; Irwin, G. R. (1973): The stress analysis of cracks handbook. Del Research Corporation, Hellertown, Pa.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Analytical Services and Materials, Inc., 107 Research Drive, 23666, Hampton, VA, USA

    I. S. Raju & T. Krishnamurthy

Authors
  1. I. S. Raju
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Krishnamurthy
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by S. N. Atluri, January 15, 1992

Rights and permissions

Reprints and permissions

About this article

Cite this article

Raju, I.S., Krishnamurthy, T. A boundary element alternating method for two-dimensional mixed-mode fracture problems. Computational Mechanics 10, 133–150 (1992). https://doi.org/10.1007/BF00369857

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00369857

Keywords

Search

Navigation