Abstract
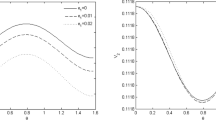
In this paper, we study the existence and the role of solitary waves in the finite amplitude instability of a layer of a second-order fluid flowing down an inclined plane. The layer becomes unstable for disturbances of large wavelength for a critical value of Reynolds number which decreases with increase in the viscoelastic parameter M. The long-term evolution of a disturbance with an initial cosinusoidal profile as a result of this instability reveals the existence of a train of solitary waves propagating on the free surface. A novel result of this study is that the number of solitary waves decreases with in crease in M. When surface tension is large, we use dynamical system theory to describe solitary waves in a moving frame by homoclinic trajectories of an associated ordinary differential equation.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Astarita G, Marucci G (1974) Principles of Non-Newtonian Fluid Mechanics, McGraw Hill
Benjamin TB (1957) Wave formation in laminar flow down an inclined plane. J Fluid Mech 2:554–574
Benney DJ (1966) Long waves on liquid films. J Math Phys 45:150–155
Bishop AR, Schneider T (eds) (1978) Solitons and Condensed Matter Physics, Springer Verlag
Coleman BD, Noll W (1960) An approximation theorem for functionals, with applications in continuum mechanics. Arch Rat Mech Anal 6:355–370
Cousins RR (1972) Stability of plane Poiseuille flow to finite-amplitude disturbances in viscoelastic fluids. Int J Eng Sci 10:511–524
Dandapat BS, Gupta AS (1978) Long waves on a layer of a visco-elastic fluid down an inclined plane. Rheo Acta 17:492–499
Gupta AS (1967) Stability of a visco-elastic liquid film flowing down an inclined plane. J Fluid Mech 28:17–28
Gupta AS, Rai L (1968) Note on the stability of a visco-elastic liquid film flowing down an inclined plane. J Fluid Mech 33:87–91
Kapitza PL, Kapitza SP (1949) Collected Works, Pergamon
Landau LD, Lifshitz EM (1959) Fluid Mechanics, Pergamon
Lin SP (1969) Finite amplitude stability of a parallel flow with a free surface. J Fluid Mech 36:113–126
Lockett FJ (1969) On Squire's theorem for viscoelastic fluids. Int J Eng Sci 7:337–349
Markovitz H, Coleman BD (1964) Advances in Applied Mechanics. 8. Academic Press
Nakaya C (1975) Long waves on thin fluid layer flowing down an inclined plane. Phys Fluids 18:1407–1412
Oldroyd JG (1950) On the formulation of theological equations of state. Proc Roy Soc A 200:523–541
Pumir A, Manneville P, Pomeau Y (1983) On solitary waves running down an inclined plane. J Fluid Mech 135:27–50
Toda M (1989) Nonlinear Waves and Solitons, Kluwer Academic Publishers
Wiggins S (1990) Introduction to Applied Nonlinear Dynamical Systems and Chaos, Springer Verlag
Yih CS (1963) Stability of liquid flow down an inclined plane. Phys Fluids 6:321–334
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Dandapat, B.S., Gupta, A.S. Solitary waves on the surface of a viscoelastic fluid running down an inclined plane. Rheola Acta 36, 135–143 (1997). https://doi.org/10.1007/BF00366819
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00366819