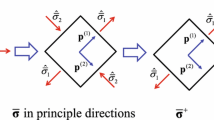
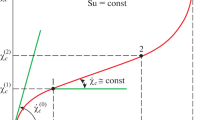
Abstract
Microcracking, damage and subsequent softening in materials introduce higher levels of nonlinearity than those for materials characterized by nonlinear elastic or classical plasticity models. Hènce, implementation of such advanced models that allow for the foregoing effects require special considerations in terms of the analysis of the characteristics of the model, convergence during plastic deformations, and time integration schemes that consider the nonlinearity.
This paper describes a damage model, a special scheme involving drift correction and the generalized time finite element (GTFEM) scheme for time integration for dynamic analysis. The main objective is to examine the model and develop schemes that can lead to consistent and reliable predictions from computational procedures. Toward this aim, (1) the damage model is analyzed with respect to its convergence behavior with mesh refinement, (2) a special drift correct scheme is implemented for the plasticity based model, (3) the generalized time finite element method (GTFEM) is implemented in the nonlinear dynamic finite element procedure for time integration and compared with the Newmark method, and (4) the damage model, the drift correction scheme and the GTFEM are verified by solution of representative static and dynamic problems involving a material (concrete) that experiences damage and softening, including verification with respect to behavior of concrete in the laboratory.
Similar content being viewed by others
References
Armaleh, S.; Desai, C. S. (1990): Modelling including testing of cohesionless soils using disturbed state concept. Report to NSF. Dept. of Civil Eng. and Eng. Mech., Univ. of Arizona, Tucson, Ariz., USA
Bazant, Z. P.; Cedolin, L. (1991): Stability of structure, Chapter 13. Oxford: Oxford University Press
Bazant, Z. P.; Lin, F. B. (1988): Nonlocal yield limit degradation. Int. J. Num. Methods in Eng. 26, 1805–1823
Bowen, R. M. (1969): Thermochemistry of reacting materials. J. Chem. Physics 50
Desai, C. S. (1974): A consistent finite element technique for work-softening behavior. Proc. Int. Conf. on Computational Methods in Nonlinear Mechanics. J. T. Oden et al. (eds.) Austin, Tex., USA
Desai, C. S. (1987): Further on unified hierarchical models based on alternative correction or damage approach. Report. Dept. of Civil Eng. and Eng. Mech., Univ. of Arizona, Tucson, Ariz., USA
Desai, C. S. (1990): Modelling, testing and implementation of numerical models and their application in practice. CISM Courses and Lectures No. 311, Int. Ctr. for Mech. Sci. Vienna: Springer
Desai, C. S. (1991): Incorporation of averaging over constant area, and relative motions of intact and damaged materials in damage and disturbed state models. Report. Dept. of Civil Eng. and Eng. Mech., Univ. of Arizona, Tucson, Ariz., USA
Desai, C. S., Kujawski, J., Miedzialowski, C.; Ryzynski, N. (1987): Improved time integration of nonlinear dynamic problems. Comp. Meth. Appl. Mech. Eng. 62, 155–168
Desai, C. S.; Ma, Y. (1992): Modelling of joints and interfaces using the disturbed state concept. Int. J. Num. Analyt. Meth. in Geomech. 16, 623–653
Desai, C. S.; Somasundaram, S.; Frantziskonis, G. (1986): A hierarchical approach for constitutive modelling of geologic materials. Int. J. Num. Analyt. Mech. in Geomech. 10, 225–257
Desai, C. S.; Wathugala, G. W., Sharma, K. G.; Woo, L. (1990): Factors affecting reliability of computer solutions with hierarchical single surface constitutive models. Computer Meth. in Appl. Mech. and Eng. 82, 115–137
Faruque, M. O.; Desai, C. S. (1985): Implementation of a general constitutive model for geologic materials. Int. J. Num. Analyt. Meth. Geomech. 9, 415–436
Frantziskonis, G.; Desai, C. S. (1987): Constitutive model with strain softening. Int. J. Solids Structures 23, No. 6
Jennings, P. C. (1964): Periodic response of ageneral yielding structure. J. Eng. Mech. Div., ASCE 90, 131–166
Kachanov, L. M. (1958): The theory of creep. (English Translation edited by Kennedy, A. J.) Chs. IX and X. National Lending Library, Boston
Kujawski, J.; Desai, C. S. (1984): Generalized time finite element algorithm for nonlinear dynamic problems. Eng. Comp. 1, 247–251
Mühlhaus, H. B.; Vardoulakis, I. (1987) The thickness of shear bands in granular materials. Geotechniques 37, No. 3, 271–283
Ortiz, M.; Simo, J. C. (1986): An analysis of a new class of integration algorithms for elastic-plastic constitutive relations. Int. J. Num. Meth. in Eng. 23, 353–366
Potts, D. M.; Gens, A. (1985): A critical assessment of methods of correcting for drift from the yield surface in elasto-plastic finite element analysis. Int. J. Num. Analyt. Methods Geomech 9, 149–159
Ramberg, W.; Osgood, W. R. (1943): Description of stress-strain curves by three parameters. Technical Note 902, NACA
Van Mier, J. G. M. (1984): Strain softening of concrete under multiaxial loading conditions. Doctoral dissertation. The Netherlands: Eindoven, Univ. of Technology
Wathugala, G. W.; Desai, C. S. (1990): Dynamic analysis of nonlinear porous media with anisotropic hardening constitutive model and application to field tests on piles in saturated clay. Report to NSF. Dept. of Civil Eng. and Eng. Mech., Univ. of Arizona, Tucson, Ariz., USA
Woo, L.; Desai, C. S. (1991). Dynamic analysis for nonlinear materials including strain-softening. Report to NSF. Department of Civil Eng. and Eng. Mech., Univ. of Arizona, Tucson, Ariz., USA
Author information
Authors and Affiliations
Additional information
Communicated by S. N. Atluri, April 14, 1992
Rights and permissions
About this article
Cite this article
Desai, C.S., Woo, L. Damage model and implementation in nonlinear dynamic problems. Computational Mechanics 11, 189–206 (1993). https://doi.org/10.1007/BF00350050
Issue Date:
DOI: https://doi.org/10.1007/BF00350050