Abstract
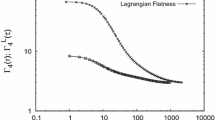
In 1952 Lighthill (1952) developed a theory for determining the sound generated by a turbulent motion of a fluid. With some statistical assumptions, Proudman (1952) applied this theory to estimate the acoustic power of isotropic turbulence. Recently, Lighthill established a simple relationship that relates the fourth-order retarded-time and space covariance of his stress tensor to the corresponding second-order covariance and the turbulent flatness factor, without making statistical assumptions for a homogeneous turbulence. Lilley (1994) revisited Proudman's work and applied the Lighthill relationship to evaluate the radiated acoustic power directly from isotropic turbulence. After choosing the time separation dependence in the two-point velocity time and space covariance based on the insights gained from direct numerical simulations, Lilley concluded that the Proudman constant is determined by the turbulent flatness factor and the second-order spatial velocity covariance. In order to estimate the Proudman constant at high Reynolds numbers, we analyzed a unique data set of measurements in a large wind tunnel and atmospheric surface layer that covers a range of the Taylor microscale-based Reynolds number 2.0×103≤R λ≤12.7×103. Our measurements demonstrate that the Lighthill relationship is a good approximation, providing additional support to Lilley's approach. The flatness factor is found between 2.7 and 3.3 and the second-order spatial velocity covariance is obtained. Based on these experimental data, the Proudman constant is estimated to be 0.68–3.68.
Similar content being viewed by others
References
Batchelor, G.H. (1953). The Theory of Homogeneous Turbulence, Cambridge University Press, Cambridge.
Hinze, J.O. (1975). Turbulence, McGraw Hill, New York.
Kaŕmań, T., von, and Howarth, L. (1938). On the statistical theory of isotropic turbulence, Proc. Roy. Soc. London Ser. A, 164, 192.
Karyakin, M. Yu., Kuznetsov, V.R., and Praskovsky, A.A. (1991). Experimental verification of the hypothesis of fine-scale isotropy of turbulence, Fluid Dynamics, 26, 658.
Lighthill, M.J. (1952). On sound generated aerodynamically: 1. General theory, Proc. Roy. Soc. London Ser. A, 211, 1107.
Lighthill, M.J. (1993). An estimate of the covariance of T xxwithout using statistical assumptions. See Lilley, G.M., On the noise radiated from a turbulent high speed jet, Appendix 1, in Computational Aeroacoustics (edited by Hardin, J.C., and Hussaini, M.Y.), Springer-Verlag, New York.
Lilley, G.M. (1994). The radiated noise from isotropic turbulence revisited, Theoret. Comput. Fluid Dynamics, 6, 281.
Oncley, S. (1992). TKE dissipation measurements during the FLAT experiments, Proc. 10th Symp. on Turbulence and Diffusion, p. 165.
Praskovsky, A.A., and Oncley, S. (1994). Measurements of the Kolmogorov constant and intermittency exponent at very high Reynolds numbers, Phys. Fluids, 6, 2886.
Praskovsky, A.A., Gledzer, E.B., Karyakin, M.Yu., and Zhou, Y. (1993). The sweeping decorrelation hypothesis and energy-inertial scale interaction in high Reynolds number flows, J. Fluid Mech., 248, 493.
Proudman, I. (1952). The generation of noise by isotropic turbulence, Proc. Roy. Soc. London Ser. A, 214, 119.
Sarkar, S., and Hussaini, M.Y. (1993). Computation of the sound generated by isotropic turbulence, ICASE Report 93-74. (Submitted to J. Fluid Mech.)
Stewart, R.W., and Townsend, A.A. (1951). Similarity and self-preservation in isotropic turbulence, Phil Trans. Roy. Soc. London Ser A, 243, 359.
Townsend, A.A. (1956). The Structure of Turbulent Shear Flow, Cambridge University Press, Cambridge.
Author information
Authors and Affiliations
Additional information
Communicated by Jackson R. Herring
This research was supported by the National Aeronautics and Space Administration under NASA Contract No. NAS1-19480 while the first author was in residence at the Institute for Computer Applications in Science and Engineering (ICASE), NASA Langley Research Center, Hampton, VA 23665, U.S.A.
The National Center for Atmospheric Research is sponsored by the National Science Foundation.
Rights and permissions
About this article
Cite this article
Zhou, Y., Praskovsky, A. & Oncley, S. On the Lighthill relationship and sound generation from isotropic turbulence. Theoret. Comput. Fluid Dynamics 7, 355–361 (1995). https://doi.org/10.1007/BF00312414
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00312414