Summary
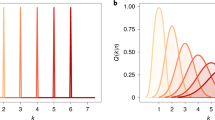
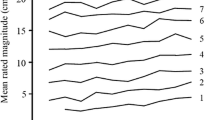
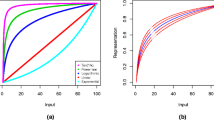
Two experiments were conducted to study the number biases of subjects in situations not involving the usual psychophysical stimuli. In Exp. I subjects were asked to generate numbers (within boundary conditions) they thought other people would produce under the same conditions. In Exp. II only a single lower boundary (e.g., 1,10 or 100) was employed and subjects generated a set of numbers larger than the boundary. Results suggested that definite number biases exist. Multiples of 1, 10, 100 and to a lesser extent 5, 50 and 500 dominate and are appropriate to the log cycle. That is, multiples of 1 occur most often in the cycle 1–10, multiples of 10 in the cycle 10–100, etc. The implications of these results are noted for several psychophysical theories.
Similar content being viewed by others
References
Attneave, F.: Perception and related areas. In: Koch, S. (Ed.): Psychology: A study of a science, Vol. 4, pp. 619–659. New York: McGraw-Hill 1962
Baird, J. C.: A cognitive theory of psychophysics. I. Information transmission, partitioning, and Weber's law. Scand. J. Psychol. 11, 35–46 (1970a)
Baird, J. C.: A cognitive theory of psychophysics. II. Fechner's law and Stevens' law. Scand. J. Psychol. 11, 89–102 (1970b)
Baird, J. C.: Information processing in alternative visual spaces. Chapter in: Baird, J. C. (Ed.): Human space perception: Proceedings of the Dartmouth conference. Psychonomic Monogr. Suppl. 3, (Whole No. 13) (1970c)
Baird, J. C.: Psychophysical analysis of visual space. London: Pergamon 1970d
Baird, J. C., Lewis, C., Romer, D.: Relative frequencies of numerical responses in ratio estimation. Percept. Psychophys. 8, 358–362 (1970)
Baird, J. C., Kreindler, M., Jones, K.: Generation of multiple ratio scales with a fixed stimulus attribute. Percept. Psychophys. 9, 399–403 (1971)
Banks, W. P.: A new psychophysical ratio scaling technique: Random production. Bull. Psychonom. Soc. 1, 273–275 (1973)
Banks, W. P., Hill, D. K.: The apparent magnitude of number scaled by random production. J. exp. Psychol. Monogr. 102 (No. 2) (1974)
Curtis, D. W.: Magnitude estimations and category judgments of brightness and brightness intervals: A two-stage interpretation. J. exp. Psychol. 83, 201–208 (1970)
Curtis, D. W., Attneave, F., Harrington, T. L.: A test of a two-stage model of magnitude judgment. Percept. Psychophys. 3, 25–31 (1968)
Eagleston, O. W., Lipford, E. J.: A study of number choices. J. genet. Psychol. 31, 129–133 (1944)
Ekman, G.: Is the power law a special case of Fechner's law? Perceptual and Motor Skills 19, 730 (1964)
Ekman, G., Hosman, B.: Note on subjective scales of number. Perceptual and Motor Skills 21, 101–102 (1965)
Ekman, G., Hosman, B., Lindman, R., Ljungberg, L., Åkesson, C. A.: Interindividual differences in scaling performance. Perceptual and Motor Skills 26, 815–823 (1968)
Engen, T., Ross, B. M.: Effect of reference number on magnitude estimation. Percept. Psychophys. 1, 74–76 (1966)
Fechner, G. E.: Elemente der Psychophysik, Bd. II. Leipzig: Breitkopf und Hartel 1907
Galton, F.: Visualized numerals. J. anthropol. Inst. 10, 85–97 (1880)
Heywood, S.: The popular number seven or number preference. Perceptual and Motor Skills 34, 357–358 (1972)
McGill, W.: The slope of the loudness function: A puzzle. In: Gulliksen, H., Messick, S. (Eds.): Psychological scaling: Theory and applications. New York: Wiley 1960
Rosner, B. S.: The power law and subjective scales of number. Perceptual and Motor Skills 21, 42 (1965)
Ross, B. M., Engen, T.: Effects of round number preferences in a guessing task. J. exp. Psychol. 58, 462–468 (1959)
Ross, S., Kohl, D. M.: Perceptual factors in number choices. J. genet. Psychol. 39, 39–47 (1948)
Rule, S. J.: Equal discriminability scale of number. J. exp. Psychol. 79, 35–38 (1969)
Stevens, S. S.: On the operation known as judgment. Amer. Scientist 54, 385–401 (1966)
Teghtsoonian, M., Teghtsoonian, R.: How repeatable are Stevens' power law exponents for individual subjects? Percept. Psychophys. 10, 147–149 (1971)
Teghtsoonian, R.: On the exponents in Stevens' law and the constant in Ekman's law. Psychol. Rev. 78, 71–80 (1971)
Wagenaar, W. A.: Generation of random sequences by human subjects.: A critical survey of the literature. Psychol. Bull. 77, 65–72 (1972)
Winick, C.: Preference for individual digits. J. genet. Psychol. 67, 271–281 (1962)
Wong, R.: Effect of the modulus on estimates of magnitude of linear extent. Amer. J. Psychol. 76, 511–512 (1963)
Yule, G. U.: On reading a scale. J. roy. statist. Soc. 90, 570 (1927)
Author information
Authors and Affiliations
Additional information
We thank Charles Lewis of the University of Illinois for advice on statistical problems.
Rights and permissions
About this article
Cite this article
Baird, J.C., Noma, E. Psychophysical study of numbers. Psychol. Res 37, 281–297 (1975). https://doi.org/10.1007/BF00309723
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00309723