On optimal intrinsic growth rates for populations in periodically changing environments

Summary

The theory developed here applies to populations whose size x obeys a differential equation,

$$\dot x = r(t)xF(x,t)$$

in which r and F are both periodic in t with period p. It is assumed that the function r, which measures a population's intrinsic rate of growth or intrinsic rate of adjustment to environmental change, is measurable and bounded with a positive lower bound. It is further assumed that the function F, which is determined by the density-dependent environmental influences on growth, is such that there is a closed interval J, with a positive lower bound, in which there lies, for each t, a number K(t) for which

$$F(K(t),t) = 0$$

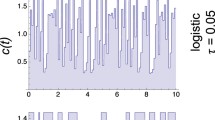
and, as functions on J × ℝ, F is continuous, while ∂F/∂x is continuous, negative, and bounded. Because x(t) = 0, > 0, or < 0 in accord with whether K(t) = x(t), K(t) > x(t), or K(t) < x(t), the number K(t) is called the “carrying capacity of the environment at time t”. The assumptions about F imply that the number K(t) is unique for each t, depends continuously and periodically on t with period P, and hence attains its extrema, K _min and K _max. It is, moreover, easily shown that the differential equation for x has precisely one solution x ^* which has its values in J and is bounded for all t in ℝ; this solution is of period p, is asymptotically stable with all of J in its domain of attraction, and is such that its minimum and maximum values, x ^*_min and x ^*_max , obey

$$K_{min} \leqslant x_{min}^* \leqslant x_{max}^* \leqslant K_{max}^* .$$

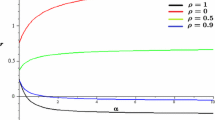
The following question is discussed: If the function F is given, and the function r can be chosen, which choices of r come close to maximizing, x ^*_min ? The results obtained yield a procedure for constructing, for each F and each ɛ > 0, a function r such that x ^*_min > K _max − ɛ.