Skip to main content
SpringerLink
Log in

The effect of time lags on the stability of the equilibrium state of a population growth equation

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Summary

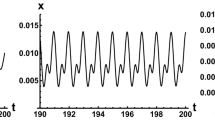
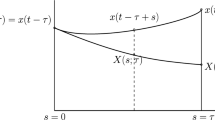
A scalar integrodifferential equation is considered which describes a single self-regulating species. Three results are presented towards showing that the ‘carrying capacity’ equilibrium state becomes unstable as the self-regulating mechanism acts after a longer time lag.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ahlfors, L. V.: Complex Analysis, 2nd Edition, New York: McGraw-Hill (1953)

    Google Scholar 

  2. Cushing, J. M.: Periodic solutions of Volterra's population equation with hereditary effects, Siam J. Applied Math., Vol. 31, No. 2, September, 1976

  3. Hadeler, K. P.: On the stability of the stationary state of a population growth equation with time-lag, J. Math. Biology 3, 197–201 (1976)

    Google Scholar 

  4. May, R. M.: Stability and Complexity in Model Ecosystems, Princeton: University Press (1973)

    Google Scholar 

  5. Walther, H. O.: On a transcendental equation in the stability analysis of a population growth model, J. Math. Biology 3, 187–195 (1976)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Virginia Polytechnic Institute and State University, 24061, Blacksburg, Virginia, USA

    Harlan W. Stech

Authors
  1. Harlan W. Stech
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Stech, H.W. The effect of time lags on the stability of the equilibrium state of a population growth equation. J. Math. Biology 5, 115–120 (1978). https://doi.org/10.1007/BF00275894

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00275894

Keywords

Search

Navigation