Abstract
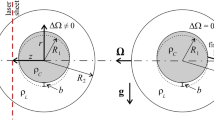
The interfacial stability of rotating core-annular flows is investigated. The linear and nonlinear effects are considered for the case when the annular region is very thin. Both asymptotic and numerical methods are used to solve the flow in the core and film regions which are coupled by a difference in viscosity and density. The long-time behavior of the fluid-fluid interface is determined by deriving its nonlinear evolution in the form of a modified Kuramoto-Sivashinsky equation. We obtain a generalization of this equation to three dimensions. The flows considered are applicable to a wide array of physical problems where liquid films are used to lubricate higher- or lower-viscosity core fluids, for which a concentric arrangement is desired. Linearized solutions show that the effects of density and viscosity stratification are crucial to the stability of the interface. Rotation generally destabilizes nonaxisymmetric disturbances to the interface, whereas the centripetal forces tend to stabilize flows in which the film contains the heavier fluid. Nonlinear effects allow finite-amplitude helically traveling waves to exist when the fluids have different viscosities.
Similar content being viewed by others
References
Batchelor, G.K., and Gill, A.E. (1962), Analysis of the Stability of Axisymmetric Jets, J. Fluid Mech., Vol. 14, pp. 529–551.
Blennerhassett, P.J. (1980), The Generation of Waves by Wind, Philos. Trans. Roy. Soc. London Ser. A, Vol. 298, pp. 451–493.
Charles, M.E., Govier, G.W., and Hodgson, G.W. (1966), The Horizontal Pipeline Flow of Equal Density of Oil-Water Mixtures, Canad. J. Chem. Engrg., Vol. 39, pp. 17–36.
Chen, K., Bai, R., and Joseph, D.D. (1990), Lubricated Pipelining, Part 3: Stability of Core-Annular Flow in Vertical Pipes, J. Fluid Mech., Vol. 214, pp. 251–286.
Frenkel, A.L., Babchin, A.J., Livich, B.G., Shlang, T., and Sivashinsky G.I. (1987), Annular Flows Can Keep Unstable Films from Breaking Up: Nonlinear Saturation of Capillary Instability, J. Colloid. Interface Sci., Vol. 115, pp. 225–233.
Georgiou, E., Maldarelli, C., Papageorgiou, D.T., and Rumschitzki, D.S. (1992), An Asymptotic Theory for the Linear Stability of Core-Annular Flow in the Thin Annular Limit, J. Fluid Mech., Vol. 243, pp. 653–677.
Hickox, C.E. (1971), Instability Due to Viscosity and Density Stratification in Axisymmetric Pipe Flow, Phys. Fluids, Vol. 14, pp. 251–262.
Hooper, A.P., and Boyd, W.G.C. (1983), Shear Flow Instability at the Interface Between Two Viscous Fluids. J. Fluid Mech., Vol. 128, pp. 507–528.
Hu, H.H., and Joseph, D.D. (1989), Lubricated Pipelining: Stability of Core-Annular Flow, Part 2, J. Fluid. Mech., Vol. 205, pp. 359–396.
Hu, H.H., and Joseph, D.D. (1989), Stability of Core-Annular Flow in a Rotating Pipe, Phys. Fluids (A), Vol. 1, pp. 1677–1685.
Joseph, D.D. (1976), Stability of Fluid Motions, Vol. 2, Springer-Verlag, Berlin.
Joseph, D.D., Renardy, M., and Renardy, Y. (1984), Instability of the Flow of Two Immiscible Liquids with Different Viscosities in a Pipe, J. Fluid Mech., Vol. 141, pp. 309–317.
Lamb, H. (1936), Hydrodynamics, Cambridge University Press, Cambridge.
Miesen, R., Beijnon, G., Duijvestijn, P.E.M., Oliemans, R.V.A., and Verheggen, T. (1992), Interfacial Waves in Core-Annular Flow, J. Fluid Mech., Vol. 238, pp. 97–117.
Papageorgiou, D.T., Maldarelli, C., and Rumschitzki, D.S. (1990), Nonlinear Interfacial Stability of Core-Annular Flows, Phys. Fluids (A), Vol. 2, No. 3, pp. 340–352.
Papageorgiou, D.T., and Smyrlis, Y.S. (1991), The Route to Chaos for the Kuramoto-Sivashinsky Equation. Theoret. Comput. Fluid Dynamics, Vol. 3, No. 1, pp. 15–42.
Papageorgiou, D.T., and Smyrlis Y.S. (1991), Predicting Chaos for Infinite-Dimensional Dynamical Systems: the Kuramoto-Sivashinsky Equation, a Case Study, Proc. Nat. Acad. Sci., USA, Vol. 88, No. 24, pp. 11129–11132.
Preziosi, L., Chen, K., and Joseph, D.D. (1989), Lubricated Pipelining: Stability of Core-Annular Flow, J. Fluid Mech., Vol. 201, pp. 323–356.
Renardy, Y. (1985), Instability at the Interface Between Two Shearing Fluids in a Channel, Phys. Fluids, Vol. 28, pp. 3441–3443.
Yih, C.S. (1967), Instability Due to Viscosity Stratification, J. Fluid Mech., Vol. 27, pp. 337–352.
Author information
Authors and Affiliations
Additional information
Communicated by M.Y. Hussaini
This research was partially supported by the National Aeronautics and Space Administration under NASA Contract No. NAS1-18605 while the second author was in residence at the Institute for Computer Applications in Science and Engineering (ICASE), NASA Langley Research Center, Hampton, VA 23665. This work was also supported by the Science and Engineering Research Council.
Rights and permissions
About this article
Cite this article
Coward, A.V., Hall, P. On the nonlinear interfacial instability of rotating core-annual flow. Theoret. Comput. Fluid Dynamics 5, 269–289 (1993). https://doi.org/10.1007/BF00271423
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00271423