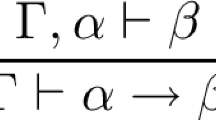Skip to main content
SpringerLink
Log in

Quantum logical calculi and lattice structures

  • Article
  • Published:
Journal of Philosophical Logic Aims and scope Submit manuscript

Abstract

In a preceding paper [1] it was shown that quantum logic, given by the tableaux-calculus T eff, is complete and consistent with respect to the dialogic foundation of logics. Since in formal dialogs the special property of the ‘value-definiteness’ of propositions is not postulated, the calculus T eff represents a calculus of effective (intuitionistic) quantum logic.

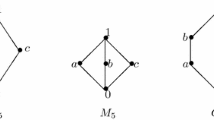
Beginning with the tableaux-calculus the equivalence of T eff to calculi which use more familiar figures such as sequents and implications can be investigated. In this paper we present a sequents-calculus of Gentzen-type and a propositional calculus of Brouwer-type which are shown to be equivalent to T eff. The effective propositional calculus provides an interpretation for a lattice structure, called quasi-implicative lattice. If, in addition, the value-definiteness of quantum mechanical propositions is postulated, a propositional calculus is obtained which provides an interpretation for a quasi-modular orthocomplemented lattice which, as is well-known, has as a model the lattice of subspaces of a Hilbert space.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Bibliography

  1. Stachow, E.-W., Journal of Philosophical Logic 5 (1976).

  2. Kleene, S. D., Introduction to Metamathematics, North-Holland Publ. Co., Amsterdam, 1964.

    Google Scholar 

  3. Lorenzen, P., Formale Logik, de Gruyter & Co., Berlin, 1970, p. 80, (Engl. ed.:Formal Logic, Reidel Publ. Co., Dordrecht, 1965, p. 56).

    Google Scholar 

  4. Lorenz, K., Arch. f. Math. Logik und Grundlagenforschung 11 (1968).

  5. Beth, E. W., The Foundations of Mathematics, Amsterdam, 1959.

  6. Lorenzen, P., Einführung in die operative Logik und Kathematik, Springer-Verlag, Berlin, 1969.

    Google Scholar 

  7. Gentzen, G., ‘Untersuchungen über das logische Schließen’, Math. Z. 39 (1934).

  8. Stachow, E.-W., Dissertation, Universität zu Köln, 1975.

  9. Brouwer, L. E. J., Over de grondslagen der wiskunde (Dissertation), Amsterdam, 1907.

  10. Mittelstaedt, P., Z. Naturforsch. 27a (1972) 1358; Mittelstaedt, P. and E.-W. Stachow, Found. of Physics 4 (1974) 335.

    Google Scholar 

  11. Curry, H. B., Foundations of Mathematical Logic, McGraw-Hill Book Co., New York, 1963; Rasiova, H., An Algebraic Approach to Non-Classical Logics, North-Holland Publ. Co., Amsterdam, 1974.

    Google Scholar 

  12. Mittelstaedt, P. and E.-W. Stachow, ‘The Principle of Excluded Middle in Quantum Logic’, Journal of Philosophical Logic 7 (1978).

Download references

Author information

Author notes

  1. E. -W. Stachow

    Present address: Institut für Theoretische Physik der Universität zu Köln, Zülpicherstr. 77, 5000, Köln 41, Germany

Authors and Affiliations

  1. University of Western Ontario, London, Canada

    E. -W. Stachow

Authors
  1. E. -W. Stachow
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Stachow, E.W. Quantum logical calculi and lattice structures. J Philos Logic 7, 347–386 (1978). https://doi.org/10.1007/BF00245934

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00245934

Keywords

Search

Navigation