Skip to main content
SpringerLink
Log in

Rotation effects on a fully-developed turbulent pipe flow

  • Originals
  • Published:
Experiments in Fluids Aims and scope Submit manuscript

Abstract

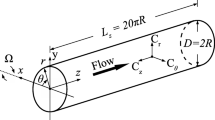
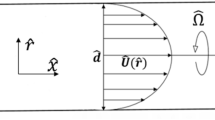
A fully-developed turbulent pipe flow is allowed to pass through a rotating pipe section, whose axis of rotation coincides with the pipe axis. At the exit end of the rotating section, the flow passes into a stationary pipe. As a result of the relaxation of surface rotation, the turbulent flow near the pipe wall is affected by extra turbulence production created by the large circumferential shear strain set up by the rapid decrease of the rotational velocity to zero at the wall. However, the flow in the most part of the pipe is absent of this extra turbulence production because the circumferential strain is zero as a result of the solid-body rotation imparted to the flow by the rotating pipe section. The combined effect of these two phenomena on the flow is investigated in detail using hot-wire anemometry techniques. Both mean and turbulence fields are measured, together with the wall shear and the turbulent burst behavior at the wall. A number of experiments at different rotational speeds are carried out. Therefore, the effects of rotation on the behavior of wall shear, turbulent burst at the wall, turbulence production and the near-wall flow can be documented and analysed in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

radius of the pipe

C f1 :

friction coefficient, \(\tau _w /\frac{1}{2}\rho W_0^2 \)

C f2 :

friction coefficient, \(\tau _w /[\frac{1}{2}\rho (W_0^2 + (a\Omega )^2 )]\)

D :

diameter of the pipe

E τw (f) :

energy spectrum of shear stress

f b :

dimensional burst frequency

\(\bar f_b \) :

normalized burst frequency, \(\frac{{f_b }}{{\left( {f_b } \right)_0 }}\)

F :

normalized kurtosis, \(\frac{{(\overline {\tau _w^{'4} } )/(\overline {\tau _w^{'2} } )^2 }}{{[(\overline {\tau _w^{'4} } )/(\overline {\tau _w^{'2} } )^2 ]_0 }}\)

k :

threshold level (used in VITA)

N s :

swirl number, aΩ/W 0

P(T) :

probability of inter-burst time, T

r :

radial coordinate

S :

normalized skewness, \(\frac{{(\overline {\tau _w^{'3} } )/(\overline {\tau _w^{'2} } )^{3/2} }}{{[(\overline {\tau _w^{'3} } )/(\overline {\tau _w^{'2} } )^{3/2} ]_0 }}\)

t :

integration time (used in VITA)

T B :

mean inter-burst time, 1/f b

\(\bar T_B \) :

normalized scaled burst frequency, \(\frac{{w_\tau ^2 T_B /v}}{{\left( {w_\tau ^2 T_B /v} \right)_0 }}\)

U, V, W :

mean velocity components in radial, circumferential and axial directions, respectively

u′, v′, w′ :

fluctuating components of velocity in radial, circumferential and axial directions, respectively

W 0 :

axial bulk mean velocity

w τ :

friction velocity, \(\left( {\frac{{\tau _w }}{\rho }} \right)^{1/2} \)

X :

distance measured from the entrance of the bend

δ :

thickness of the viscous layer

ν :

kinematic viscosity

ρ :

density of fluid

σ :

normalized standard deviation, \(\frac{{(\overline {\tau _w^{'2} } )^{1/2} }}{{(\overline {\tau _w^{'2} } )_0^{1/2} }}\)

Ω :

rotational speed of pipe in RPM

0:

condition at X/D=-18

References

  • Achia, B. U.; Thompson, P. W. 1977: Structure of the turbulent boundary layer in a drag reducing pipe flow. J. Fluid Mech. 81, 439–464

    Google Scholar 

  • Anwer, M.; So, R. M. C. 1988: Study of sublayer bursting in a curved bend. AIAA Paper 88-3581

  • Anwer, M.; So, R. M. C.; Lai, Y. G. 1989: Perturbation by and recovery from bend curvature of a fully-developed turbulent pipe flow. Phys. Fluids, in press

  • Bellhouse, B. J.; Schultz, P. L. 1966: Determination of mean and dynamic skin friction, separation and transition in low-speed flow with a thin-film heated element. J. Fluid Mech. 24, 379–400

    Google Scholar 

  • Bissonnette, L. R.; Mellor, G. L. 1974: Experiments on the behavior of an axisymmetric turbulent boundary layer with a sudden circumferential strain. J. Fluid Mech. 63, 369–413

    Google Scholar 

  • Blackwelder, R. F.; Haritonidis, J. H. 1983: Scaling of bursting frequency in a turbulent layer. J. Fluid Mech. 132, 87–103

    Google Scholar 

  • Blackwelder, R. F.; Kaplan, R. E. 1976: On the wall structure of the turbulent boundary layer. J. Fluid Mech. 76, 89–112

    Google Scholar 

  • Bogard, D. G.; Tiederman, W. G. 1986: Burst detection with single point velocity measurements. J. Fluid Mech. 162, 380–413

    Google Scholar 

  • Bogard, D. G.; Tiederman, W. G. 1987: Characteristics of ejections in turbulent channel flows. J. Fluid Mech. 179, 1–19

    Google Scholar 

  • Chen, C. P.; Blackwelder, R. F. 1978: The large scale motion in a turbulent boundary layer: a study using temperature contamination. J. Fluid Mech. 89, 1–31

    Google Scholar 

  • Corrsin, S. 1963: Turbulence: experimental methods. Handb Phys. 8, 524–590

    MathSciNet  Google Scholar 

  • Johansson, A. V.; Alfredsson, P. H. 1982: On the structure of turbulent channel flow. J. Fluid Mech. 122, 295–314

    Google Scholar 

  • Johnston, J. P.; Halleen, R. M.; Lezius, D. K. 1972: Effects of spanwise rotation on the structure of two-dimensional fully-developed turbulent channel flow. J. Fluid Mech. 56, 533–557

    Google Scholar 

  • Kikuyama, K.; Murakami, M.; Nishibori, K. 1983: Development of three-dimensional turbulent boundary layers in an axially rotating pipe. J. Fluids Eng. 105, 154–160

    Google Scholar 

  • Laufer, J. 1954: The structure of turbulence in fully developed pipe flow. NACA Report 1174

  • Ligrani, P. M.; Bradshaw, P. 1987: Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5, 407–417

    Article  Google Scholar 

  • Loehrke, R. I.; Nagib, H. M. 1976: Control of free stream turbulence by means of honeycomb. A balance between suppression and generation. J. Fluids Eng. 98, 342–353

    Google Scholar 

  • Lohmann, R. P. 1976: The response of a developed turbulent boundary layer to local transverse surface motion. J. Fluids Eng. 98, 354–363

    Google Scholar 

  • Luchick, T. S.; Tiederman, W. G. 1987: Timescale and structure of ejections and bursts in turbulent channel flows. J. Fluid Mech. 174, 529–552

    Google Scholar 

  • Lumley, J L. 1964: Passage of a turbulent stream through honeycomb of large length-to-diameter ratio. J. Basic Eng. 86, 218–220

    Google Scholar 

  • Mautner, T. S.; Van Atta, C. W. 1986: Wall shear stress measurements in the plane of symmetry of a turbulent spot. Exp. Fluids 4, 153–162

    Google Scholar 

  • Menendez, A. N.; Ramaprian, B. R. 1985: The use of flush-mounted hot film gauges to measure skin friction in unsteady boundary layers. J. Fluid Mech. 161, 139–160

    Google Scholar 

  • Murakami, M.; Kikuyama, K. 1980: Turbulent flow in axially rotating pipes. J. Fluid Eng. 102, 97–103

    Google Scholar 

  • Sabot, J.; Comte-Bellot, G. 1976: Intermittency of coherent structures in the core region of fully developed turbulent pipe flow. J. Fluid Mech. 74, 767–796

    Google Scholar 

  • Shah, D. A.; Antonia, R. A. 1987: Scaling of wall shear stress fluctuations in a turbulent duct flow. AIAA J. 25, 22–29

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mechanical and Aerospace Engineering, Arizona State University, 85287-6106, Tempe, AZ, USA

    M. Anwer & R. M. C. So

Authors
  1. M. Anwer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. M. C. So
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Anwer, M., So, R.M.C. Rotation effects on a fully-developed turbulent pipe flow. Experiments in Fluids 8, 33–40 (1989). https://doi.org/10.1007/BF00203062

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00203062

Keywords

Search

Navigation