Skip to main content
SpringerLink
Log in

Construction of Modified Taylor-Galerkin Finite Elements and its application in compressible flow computation

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

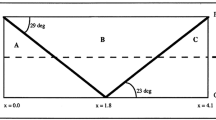
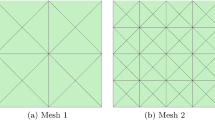
In this paper we begin with Taylor-Galerkin Finite Elements, then improve it completely and finally construct Modified Taylor-Galerkin Finite Elements. Computation is done by two methods to study two kinds of subsonic and supersonic flow field. The results show that the new one is much better than the old one.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. T. J.Oden, Adaptive Methods for Problems in Solid and Fluid Mechanics, John Wiley and Sons Ltd., London (1986).

    Google Scholar 

  2. T. J. Chung, Finite Element Analysis in Fluid Dynamics, McGraw-Hill Book Co. (1978).

  3. J. Donea and S. Giuliani, Time accurate solution of advection-diffusion problems by finite elements, Computer Methods in Applied Mechanics and Engineering, 45 (1984).

  4. T. J. Chung, Finite elements in Fluid and Heat Transfer, Krieger Publishing Company, Inc. (1991).

  5. C. Johnson, Numerical Solutions of Partial Differential Equations by the Finite Element Method, Sweden Student-litteratur (1987).

  6. T. J. R.Hughes and M.Mallet, A new finite element formulation for computational fluid dynamics: IV, A discontinuity-capturing operator for multidimensional advective-diffusive systems, Comput. Methods Appl. Mech. Eng., 58 (1986), 329–336.

    Google Scholar 

  7. ZhuGang, GuChuangang and HuQingkang, A modification of Taylor-Galerkin finite element method and its application, Applied Mathematics and Mechanics (English Ed.), 14, 12 (1993), 1173–1179.

    Google Scholar 

  8. G. Q. Xu and G. F. Zhang, Computational SUPG finite element results for incompressible Navier-Stokes equations, Journal of Aerodynamics, 9 (1991). (in Chinese)

  9. T. J. Chung, Numerical Modeling in Combustion, Taylor & Francis Inc. (1993).

  10. A.Lapidus, A detached shock calculation by second-order finite differences, Journal of Computational Physics, 2 (1967), 154–177.

    Google Scholar 

  11. Zhu Gang, Shen Mengyu, Liu Qiusheng and Wang Baoguo, Anisotropic multistage finite element method for two dimensional viscous transonic flow in turbomachinery, Acta Mechanica Sinica, 11, 1 (1995).

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Qinghua University, 100084, Beijing, P. R. China

    Zhu Gang, Shen Mengyu, Liu Qiusheng & Wang Baoguo

Authors
  1. Zhu Gang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shen Mengyu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Liu Qiusheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wang Baoguo
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by Chien Weizang and Zhou Zhewei

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gang, Z., Mengyu, S., Qiusheng, L. et al. Construction of Modified Taylor-Galerkin Finite Elements and its application in compressible flow computation. Appl Math Mech 17, 333–339 (1996). https://doi.org/10.1007/BF00193796

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00193796

Key words

Search

Navigation