Localized folding of viscoelastic layers

Abstract

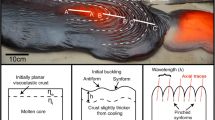
Naturally occurring fold systems are typically irregular. Although such systems may sometimes be approximated by a periodic geometry, in reality they are commonly aperiodic. Ord (1994) has proposed that naturally occurring fold systems may display spatial chaos in their geometry. Previous work has indicated that linear theories for the formation of fold systems, such as those developed by Biot (1965), result in strictly periodic geometries. In this paper the development of spatially chaotic geometries is explored for a thin compressed elastic layer embedded in a viscoelastic medium which shows elastic softening. In particular, it is shown that spatially localized forms of buckling can develop and the evolution of these systems in the time domain is presented. A nonlinear partial differential equation, fourth order in a spatial variable and first order in time, is found to govern the evolution. A related nonlinear fourth-order ordinary differential equation governs an initial elastic phase of folding. The latter equation belongs to a class with spatially chaotic solutions. The paper reviews the implications of localization in the geological framework, and draws some tentative conclusions about the development of spatial chaos. Crudely arrived-at, yet plausible, evolutionary time plots under the constraint of constant applied end displacement are presented. Emphasis throughout is on phenomenology, rather than underlying mathematics or numerics.