Abstract
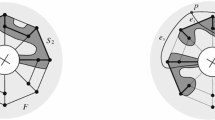
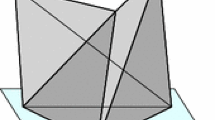
A weakly neighborly polyhedral map (w.n.p. map) is a 2-dimensional cell-complex which decomposes a closed 2-manifold without a boundary, such that for every two vertices there is a 2-cell containing them. We prove that there are just five distinct w.n.p. maps on the torus, and that only three of them are geometrically realizable as polyhedra with convex faces.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Altshuler, A., ‘Polyhedral Realizations in R 3 of Triangulations of the Torus and 2-Manifolds in Cyclic 4-Polytopes’, Discrete Math. 1 (1971), 211–238.
Altshuler, A., ‘Hamiltonian Circuits in Some Maps on the Torus’, Discrete Math. 1 (1972), 299–314.
Altshuler, A., ‘Construction and Enumeration of Regular Maps on the Torus’, Discrete Math. 4 (1973), 201–217.
Altshuler, A. and Brehm, U., ‘A Non-Schlegelian Map on the Torus’, Mathematika 31 (1984), 83–88.
Altshuler, A. and Brehm, U., ‘Non-existence of Weakly Neighborly Polyhedral Maps on the Orientable 2-Manifold of Genus 2’, J. Combinatorial Theory, Ser. A (to appear).
Brehm, U. and Altshuler, A., ‘On Weakly Neighborly Polyhedral Maps of Arbitrary Genus’, Israel J. Math. (to appear).
Barnette, D., ‘Polyhedral Maps on 2-Manifolds’, in Convexity and Related Combinatorial Geometry (Proc. Second Univ. of Oklahoma Conf.), eds D. C. Kay and M. Breen, Marcel Dekker Inc., 1982, pp. 7–19.
Császár, A., ‘A Polyhedron without Diagonals’, Acta Sci. Math. Szeged 13 (1949–50), 140–142.
Grünbaum, B., Convex Polytopes, Wiley, New York, 1967.
Möbius, A. F., Gesammelte Werke, Vol. 2, Leipzig, 1886.
Ringel, G., Map Color Theorem, Springer, 1974.
Simutis, J., ‘Geometric Realizations of Toroidal Maps’, Ph. D. Thesis, Univ. of California, Davis, 1977.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Brehm, U., Altshuler, A. The weakly neighborly polyhedral maps on the torus. Geom Dedicata 18, 227–238 (1985). https://doi.org/10.1007/BF00181222
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00181222