Abstract
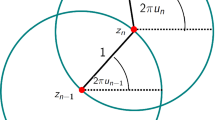
We define a regular homotopy invariant of closed curves on a surface, and give a formula for the rotation number of closed curves on torus, which is analogous to the Whitney formula for planar curves. As an application, we show a necessary condition for a Gauss word to be realized on torus.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Cairns, G. and Elton, D. M.: The planarity problem for signed Gauss words,J. Knot Theory Ramif. 2 (1993), 359–367.
Cairns, G. and Elton, D. M.: The planarity problem II, Preprint, 1994.
Carter, J. Scott: Classifying immersed curves,Proc. Amer. Math. Soc. 111 (1991), 281–287.
Chillingworth, D. R. J.: Winding numbers on Surfaces, I,Math. Ann. 196 (1972), 218–249.
Grünbaum, B. and Shephard, G. C.: Rotation and winding numbers for planar polygons and curves,Trans. Amer. Math. Soc. 322 (1990), 169–187.
McIntyre, M. and Cairns, G.: A new formula for winding number,Geom. Dedicata 46 (1993), 149–159.
Reinhart, B. L.: The winding number on two manifolds,Ann. Inst. Fourier, Grenoble 10 (1960), 271–283.
Smale, S.: Regular curves on Riemannian manifolds,Trans. Amer. Math. Soc. 87 (1958), 492–512.
Whitney, H.: On regular closed curves in the plane,Comput. Math. 4 (1937), 276–286.
Youngs, J. W. T.: Minimal imbeddings and the genus of a graph,J. Math. Mech. 12 (1963), 303–315.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Tanio, H., Kobayashi, O. Rotation numbers for curves on a torus. Geom Dedicata 61, 1–9 (1996). https://doi.org/10.1007/BF00149414
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00149414