On arbitration schemes for a wealth distribution problem

Abstract

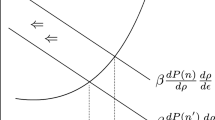
This paper develops an arbitration scheme for resolving a distribution of wealth problem by applying Nash's assumptions to marginal rather than to total utilities. The problem considered is that of distributing a fixed amount of wealth between two claimants, and the paper compares properties of this problem's Nash solution with those of the marginal utility solution. The Nash solution is shown to emphasize application of symmetry considerations to the status quo ante, the marginal utility solution their application to the players' post arbitration positions (as measured by functions that fully describe the players' utilities but that are independent of positive linear transformations). It is argued that while the Nash assumptions are appropriate for many arbitration problems in which a solution reflects the players' status quo ante positions, the marginal utility assumptions are useful when it is desired that a solution attempt to minimize post-arbitration differences between the players' positions. The latter seems to be preferable in contexts where an arbitrator weights the solution's effects on out-comes more heavily than he weights considerations of the status quo ante. Examples are situations such as those involving income redistribution, where attempts to reduce inequality may guide the redistribution decisions. The effects on each type of solution of changes in the status quo ante are also investigated and related to the risk preference properties of the players' utilities.