Abstract
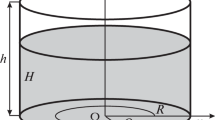
Free surface flow in a cylindrical container with steadily rotating bottom cap is investigated. A regular domain perturbation in terms of the angular velocity of the bottom is used. The flow field is made up of the superposition of azimuthal and meridional fields. The meridional field is solved both by biorthogonal series and a numerical algorithm. The free surface on the liquid is determined at the lowest significant order. The aspect ratio of the cylinder may generate a multiple cell structure in the meridional plane which in turn shapes the free surface.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
T. Von Kármán, Uber laminare und turbulente Reibung.ZAMM 1 (1921) 233–252.
W.G. Cochran, The flow due to a rotating disc.Proceedings of Cambridge Philosophical Society 30 (1934) 365–375.
U.T. Bödewadt, Die Drehströmung über festem Grunde.ZAMM 20 (1940), 241–253.
G.K. Batchelor, Note on a class of solutions of the Navier-Stokes equations representing steady rotationally-symmetric flow.Quarterly Journal of Mechanics and Applied Mathematics 4 (1951), 29–41.
K. Stewartson, On the flow between two rotating coaxial discs.Proceedings of Cambridge Philosophical Society 49 (1953), 333–341.
J.F. Brady and L. Durlofsky, On rotating disk flow.Journal of Fluid Mechanics 175 (1987),363–394.
P.J. Zandbergen and D. Dijkstra, Von Kármán swirling flows. In: J.L. Lumley, M. Van Dyke and H.L. Reed (eds),Annual Review of Fluid Mechanics 19 (1987), 465–491.
F. Schultz-Grunow, Der Reibungswiderstand rotierender Scheiben in Gehausen.ZAMM 14 (1935) 191–204.
H.P. Pao, A numerical computation of a confined rotating flow.Journal of Applied Mechanics 37 (1970), 480–487.
U. Cederlöf, Free-surface effects on spin-up.Journal of Fluid Mechanics 187 (1988), 395–407.
J. O'Donnell and P.F. Linden, Free-surface effects on the spin-up of fluid in a rotating cylinder.Journal of Fluid Mechanics 232 (1991), 439–453.
J.M. Hyun, Flow in an open tank with a free surface driven by the spinning bottom.Journal of Fluids Engineering 107 (1985), 495–499.
D.D. Joseph and L. Sturges, The free surface on a liquid filling a trench heated from its side.Journal of Fluid Mechanics 69 (1975), 565–589.
D.D. Joseph, A new separation of variables theory for problems of Stokes flow and Elasticity. In:Trends in Applications of Pure Mathematics to Mechanics. London: Pitman (1978) pp. 129–162.
D.D. Joseph, L.D. Sturges and W.H. Warner, Convergence of biorthogonal series of biharmonic eigenfunctions by the method of Titchmarsh.Archive of Rational Mechanics and Analysis 78 (1982), 223–274.
L. Kleiser and U. Schumann, Treatment of incompressibility and boundary conditions in 3-D numerical spectral simulations of plane channel flows. In: E.H. Hirschel (ed.),Proceedings of the Third GAMM-Conference on Numerical Methods in Fluid Mechanics (1980), V. 2, 165–172.
B.L. Buzbee, F.W. Dorr, J.A. George and G.H. Golub, The direct solution of the discrete Poisson equation on irregular regions.SIAM Journal of Numerical Analysis 8 (1971), 722–734.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Siginer, A., Knight, R. Swirling free surface flow in cylindrical containers. J Eng Math 27, 245–264 (1993). https://doi.org/10.1007/BF00128966
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00128966