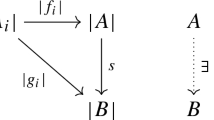
Abstract
Due to the nature of compactness, there are several interesting ways of defining compact objects in a category. In this paper we introduce and study an internal notion of compact objects relative to a closure operator (following the Borel-Lebesgue definition of compact spaces) and a notion of compact objects with respect to a class of morphisms (following Áhn and Wiegandt [2]). Although these concepts seem very different in essence, we show that, in convenient settings, compactness with respect to a class of morphisms can be viewed as Borel-Lebesgue compactness for a suitable closure operator. Finally, we use the results obtained to study compact objects relative to a class of morphisms in some special settings.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Adámek, J., Herrlich, H., and Strecker, G. E.: Abstract and Concrete Categories, Wiley, New York-Chichester-Brisbane-Toronto-Singapore, 1990.
Áhn, P. N. and Wiegandt, R.: Compactness in categories and interpretations, Preprint, 1990.
Castellini, G.: Compact objects, surjectivity of epimorphisms and compactifications, Cahiers Topologie Geom. Differentielle Categoriques 31 (1990), 53–65.
Čech, E.: Topological Spaces, Revised by Z. Frolík and M. Katětov, Academia, Praha, 1966.
Clementino, M. M.: Separação e Compacidade em Categorias, PhD Thesis, Universidade de Coimbra, 1992.
Clementino, M. M., Giuli, E., and Tholen, W.: Topology in a category: compactness, Preprint.
Dikranjan, D. and Giuli, E.: Closure operators I, Topology Appl. 27 (1987), 129–143.
Dikranjan, D. and Giuli, E.: Compactness, minimality and closedness with respect to a closure operator, in: Categorical Topology and Its Relations to Analysis, Algebra and Combinatorics, Proc. Int. Conf. Prague, World Scientific, Singapore-New Jersey-London-Hong Kong, 1988, pp. 284–296.
Dikranjan, D., Giuli, E., and Tholen, W.: Closure operators II, in: Categorical Topology and Its Relations to Analysis, Algebra and Combinatorics, Proc. Int. Conf. Prague, World Scientific, Singapore-New Jersey-London-Hong Kong, 1988, pp. 297–335.
Freyd, P. J. and Kelly, G. M.: Categories of continuous functors, I, J. Pure Appl. Algebra 2 (1972), 169–191, Erratum ibid. 4 (1974), 121.
Johnstone, P. T.: Stone Spaces, Cambridge Univ. Press, Cambridge, 1982.
MacLane, S.: Categories for the Working Mathematician, Springer-Verlag, Berlin-Heidelberg-New York, 1971.
Manes, E. G.: Compact Hausdorff objects, Topology Appl. 4 (1974), 341–360.
Sousa, L.: Orthogonality and closure operators, Cahiers Topologie Geom. Differentielle Categoriques, to appear.
Sousa, L.: α-sober spaces via the orthogonal closure operator, Applied Categ. Structures 4 (1996), 87–95 (this issue).
Author information
Authors and Affiliations
Additional information
Partial financial assistance by Centro de Matemática da Universidade de Coimbra and by a NATO Collaborative Grant (CRG 940847) is gratefully acknowledged.
Rights and permissions
About this article
Cite this article
Clementino, M.M. On categorical notions of compact objects. Appl Categor Struct 4, 15–29 (1996). https://doi.org/10.1007/BF00124111
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00124111