Skip to main content
SpringerLink
Log in

Global bifurcations in the motion of parametrically excited thin plates

  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

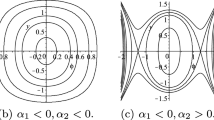
In this paper we investigate global bifurcations in the motion of parametrically excited, damped thin plates. Using new mathematical results by Kovačič and Wiggins in finding homoclinic and heteroclinic orbits to fixed points that are created in a resonance resulting from perturbation, we are able to obtain explicit conditions under which Silnikov homoclinic orbits occur. Furthermore, we confirm our theoretical predictions by numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Yang, X. L. and Sethna, P.R., ‘Local and global bifurcations in parametrically excited vibrations of nearly square plates’, International Journal of Non-Linear Mechanics 26, 1991, 199–220.

    Google Scholar 

  2. Feng, Z. C. and Sethna, P. R., ‘Symmetry-breaking bifurcations in resonant surface waves’, Journal of Fluid Mechanics 199, 1989, 495–518.

    Google Scholar 

  3. Kovačič, G. and Wiggins, S., ‘Orbits homoclinic to resonances, with an application to chaos in a model of the forced and damped Sine-Gordon equation’, Physica D 57, 1992, 185–225.

    Google Scholar 

  4. Chu, H. and Herrmann, G., ‘Influence of large amplitudes in free flexural response of an inextensional beam’, Journal of Applied Mechanics 23, 1956, 532–540.

    Google Scholar 

  5. Feng, Z. C. and Sethna, P. R., ‘Global bifurcation and chaos in parametrically forced systems with one-one resonance’, Dynamics and Stability of Systems 5, 1990, 201–225.

    Google Scholar 

  6. Gu, X. M., Sethna, P. R., and Narain, A., ‘On three-dimensional non-linear subharmonic resonant surface waves in a fluid. Part I: Theory’, Journal of Applied Mechanics, 55, 1988, 213–219.

    Google Scholar 

  7. Wiggins, S., Global Bifurcations and Chaos—Analytical Methods, Springer-Verlag, New York, 1988.

    Google Scholar 

  8. Gradshteyn, I. S. and Ryzhik, I. M., Tables of Integrals, Series and Products, Academic, CA, 1980.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Chemical and Nuclear Engineering, University of California, 93106, Santa Barbara, CA, U.S.A.

    Z. C. Feng

  2. Department of Aerospace Engineering and Mechanics, University of Minnesota, 55455, Minneapolis, MN, U.S.A.

    P. R. Sethna (Visiting Professor at University of Pisa, Italy)

Authors
  1. Z. C. Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. R. Sethna
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Feng, Z.C., Sethna, P.R. Global bifurcations in the motion of parametrically excited thin plates. Nonlinear Dyn 4, 389–408 (1993). https://doi.org/10.1007/BF00120673

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00120673

Key words

Search

Navigation