Abstract
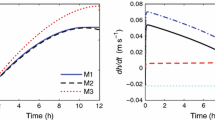
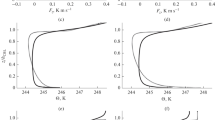
A slab model is proposed for developing the height of the mixed layer capped by stable air aloft. The model equations are closed by relating the consumption of energy (potential and kinetic) at the top of the mixed layer to the production of convective and mechanical turbulent kinetic energy within the mixed layer. By assuming that the temperature difference at the top of the mixed layer instantaneously adjusts to the actual meteorological conditions without regard to the initial temperature difference that prevailed, the model is reduced to a single differential equation which easily can be solved numerically. When the mixed layer is shallow or the atmosphere nearly neutrally stratified, the growth is controlled mainly by mechanical turbulence. When the layer is deep, its growth is controlled mainly by convective turbulence. The model is applied on a data set of the evolution of the height of the mixed layer in the morning hours, when both mechanical and convective turbulence contribute to the growth process. Realistic mixed-layer developments are obtained.
Similar content being viewed by others
References
Carson, D. J.: 1973, ‘The Development of a Dry Inversion-Capped Convectively Unstable Layer’, Quart. J. R. Meteorol. Soc. 99, 450–467.
Carson, D. J. and Smith, F. B.: 1974, ‘Thermodynamic Model for the Development of a Convectively Unstable Boundary Layer’, Advances Geophys. 18A, Academic Press, New York, pp. 111–124.
Driedonks, A. G. M.: 1982, ‘Models and Observations of the Growth of the Atmospheric Boundary Layer’, Boundary-Layer Meteorol. 23, 283–306.
Dyer, A. J.: 1974, ‘A Review of Flux Profile Relationships’, Boundary-Layer Meteorol. 7, 363–372.
Gryning, S. E. and Batchvarova, E.: 1990a, ‘Simple Model of the Daytime Boundary Layer Height’, Ninth Symposium on Turbulence and Diffusion. American Meteorological Society. April 30–May 3, 1990. Roskilde, Denmark, pp. 379–382.
Gryning, S. E. and Batchvarova, E.: 1990b, ‘Analytical Model for the Growth of the Coastal Internal Boundary Layer During Onshore Flow’, Quart. J. R. Meteorol. Soc. 116, 187–203.
Holtslag, A. A. M. and van Ulden, A. P.: 1983, ‘A Simple Scheme for Daytime Estimates of the Surface Fluxes from Routine Weather Data’, J. Climate Appl. Meteorol. 22, 517–529.
Högström, U.: 1988, ‘Non-Dimensional Wind and Temperature Profiles in the Atmospheric Surface Layer: A Re-evaluation’, Boundary-Layer Meteorol. 42, 55–78.
Kantha, L. H., Phillips, O. M., and Azad, R. S.: 1977, ‘On Turbulent Entrainment at a Stable Density Interface’, J. Fluid Mech. 79, 753–768.
Kato, H. and Phillips, O. M.: 1969, ‘On the Penetration of a Turbulent Layer into Stratified Fluid’, J. Fluid Mech. 37, 643–655.
Lilly, D. K.: 1968, ‘Models of Cloud-Topped Mixed Layers Under a Strong Inversion’, Quart. J. R. Meteorol. Soc. 94, 292–309.
Mahrt, L. and Lenschow, D. H.: 1976, ‘Growth Dynamics of the Convectively Mixed Layer’, J. Atmos. Sci. 33, 41–51.
Manins, P. C.: 1982, ‘The Daytime Planetary Boundary Layer: A New Interpretation of the Wangara Data’;. Quart. J. R. Meteorol. Soc. 108, 689–705.
Panofsky, H. A. and Dutton, J. A.: 1984, Atmospheric Turbulence, John Wiley and Sons, p. 397
Stull, R. B.: 1976, ‘The Energetics of Entrainment Across a Density Interface’, J. Atmos. Sci. 33, 1260–1267.
Tennekes, H.: 1973, ‘A Slab Model for the Dynamics of the Inversion Above a Convective Boundary Layer’, J. Atmos. Sci. 30, 558–567.
Tennekes, H. and Driedonks, A. G. M.: 1981, ‘Basic Entrainment Equations for the Atmospheric Boundary Layer’, Boundary-Layer Meteorol. 20, 515–531.
Tennekes, H. and van Ulden, A. P.: 1974, ‘Short-Term Forecasts of Temperature and Mixing Height on Sunny Days’, Symposium on Atmospheric Diffusion and Air Pollution. American Meteorological Society, September 9–13, Santa Barbara, California, pp. 35–40.
Zeman, O. and Tennekes, H.: 1977, ‘Parameterization of the Turbulent Kinetic Energy Budget at the Top of the Daytime Boundary Layer’, J. Atmos. Sci. 34, 111–123.
Zeuner, G. and Heinemann, K. (eds.): 1990, ‘Investigations on Atmospheric Dispersion of Air Pollutants after Short-Time Releases in Complex Terrain. Third Field Experiment on Atmospheric Dispersion around the Isolated Hill Sophienhöhe in August/September 1988’. Report-Jül-2388. ISSN 0336-0885. Forschungszentrum Jülich GmbH, p 273.
Zilitinkevich, S. S.: 1975, ‘Comments on a Paper by H. Tennekes’, J. Atmos. Sci. 32, 991–992.
Zilitinkevich, S. S.: 1991, Turbulent Penetrative Convection, Published by Gower Press (in press).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Batchvarova, E., Gryning, SE. Applied model for the growth of the daytime mixed layer. Boundary-Layer Meteorol 56, 261–274 (1991). https://doi.org/10.1007/BF00120423
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00120423