Thermal conductivity of superconductors in the intermediate state: Size effect in a longitudinal lamellar structure

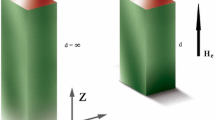
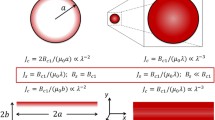
The thermal conductivity of type I superconductors has been measured in a well-defined, optically controlled intermediate-state configuration, the so-called longitudinal lamellar structure (LLS). A regular arrangement of alternating normal and superconducting lamellas is obtained in an elongated plate by applying the magnetic field obliquely (following Sharvin) and decreasing it from the critical value. The heat current is set parallel to the lamellas. Due to the peculiar reflection law governing the quasiparticle reflections at a normal-superconductor interphase boundary, the thermal conductivity of the LLS is reduced when the electronic mean free path is larger than or comparable to the width of the lamellas. As first pointed out by Andreev, the reflection occurs with vector-momentum conservation, and only the quasiparticles moving nearly parallel to the lamellas can transport heat efficiently. The corresponding reduction of the thermal conductivity is a size effect.

Systematic measurements of the thermal conductivity of the LLS in high-purity lead and tin are interpreted in terms of the size-effect model. The parameters of the model were experimentally determined in a preliminary study, to enable an unambiguous comparison with the theory. In particular, the geometrical aspects of the structures were studied using a magnetooptical technique. Interesting results on the characteristics of the LLS were obtained. The thermal conductivity data on lead essentially confirm the size-effect description. In lead below 4.2 K, heat is conducted much more efficiently by the normal lamellas than by the superconducting ones. In particular, phonon effects in the superconducting phase can be neglected and the results give information on the behavior of the normal-phase quasiparticles. The situation is different for tin, where heat transport by the lamellas of both types takes place, the heat carriers being the electrons (T ≳ 1.6 K). The discrepancy between the predictions of the size-effect model and the observed values in tin are attributed to an oversimplified calculation of the contribution of the superconducting lamellas to the conductivity. A more detailed treatment is needed, but the basic description of the thermal conductivity reduction in terms of the size effect should remain.