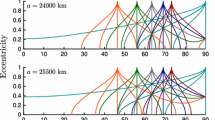
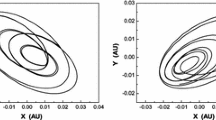
Abstract
We have investigated the pericentric resonances through which Miranda and Umbriel are believed to have passed when, due to tidal evolution, their orbital mean motions reached a 3 : 1 commensurability. Our investigation is based upon a perturbative treatment. The predictions of this theory are in good agreement with the results of numerical integrations concerning both the extend of the chaotic layers generated by the separatrices of the primary resonances and the location of the secondary resonances. The effect of tidal evolution is discussed on the bases of the adiatatic invariant theory and its extension to separatrix crossing. We recover qualitatively the mean features of the numerical experiments of Tittermore and Wisdom (1988–1989), Dermott et al (1988) and Malhotra and Dermott (1989).
Similar content being viewed by others
References
Allan, R.R.: 1969, “Evolution of Mimas-Tethis commensurability”. Astron. J.,74, 497–506.
Borderies, N., and Goldreich, P.: 1984, “A simple derivation of capture probabilities”, Celest. Mech., 32, 127–136.
Chirikov, B.V.: 1979,“A universal instability of many-dimensional oscillator systems”, Physics Reports, 52, 263–379.
Dermott, S.F., Malhotra, R. and Murray C.D.: 1988, “Dynamics of the Uranian and Saturnian satellite systems : A chaotic route to melting Miranda?”, Icarus, 76, 295–334.
Goldreich, P.: 1965, “An explanation of the frequent occurence of commensurable mean motions in the Solar system”, M.N.R.A.S., 130, 159–181.
Greenberg, R.: 1973, “Evolution of satellite resonances by tidal dissipation”, Astron. J., 78, 338–346.
Greenberg, R.: 1977, “Orbit-orbit resonances in the Solar System : Varieties and similarities”, Vistas in Astronomy, 21, 209–239.
Henrard, J.: 1982, “Capture into resonance : An extension of the use of the adiabatic invariants”, Celest. Mech., 27, 3–22.
Henrard, J.: “Resonance in the planar elliptic restricted problem”, In Long Term Behaviour of Natural and Artificial N-Body Systems, A. Roy (eded.), Kluwer Academic Publishers.
Henrard, J. : 1989, “The adiabatic invariant in Classical Mechanics”, Dynamics Reported, to be published.
Henrard, J., and Caranicolas, N. : 1989, “Motion near the 3/1 resonance of the planar elliptic restricted three body problem”, Celest. Mech., in print.
Henrard, J. and de Vleeschauwer, A.: 1988, “Sweeping through a second order resonance”, Celest. Mech., 43, 99–112.
Henrard, J. and Lemaitre, A.: 1983, “A second fundamental model for resonance”, Celest. Mech., 30, 197–218.
Henrard, J., and Lemaitre, A.: 1986, “A perturbation method for problems with two critical arguments”, Celest. Mech., 39, 213–238.
Landau, L. and Lifchitz, E. : 1960 , Mécanique, Edition en langues éetrangeres. Moscou.
Lemaitre, A.: 1984, “High order resonance in the restricted three body problem”, Celest. Mech., 32, 109–126.
Malhotra, R. and Dermott, S.F. : 1989, “The role of secondary resonances in the orbital history of Miranda”, Icarus, in print.
Peale, S.J.: 1976, “Orbital resonances in the Solar System”, Ann. Rev. Astron. Astrophys., 14, 215–245.
Peale, S.J. : 1986, “Orbital resonance, unusual configurations and exotic rotation states”, in Satellites (J. Burns and M. Matthews eds.), Univ. of Arizona Press, 159–223.
Peale, S.J.: 1988, “Speculative histories of the Uranian satellite system”, Icarus, 74, 153–171.
Peale, S.J., Cassen, P. and Reynolds, R.: 1979, “Melting of lo by tidal dissipation”, Science, 203, 892–894.
Sinclair, A.T.: 1972, “On the origin of commensurabilities amongst the satellite of Saturn”, M.N.R.A.S., 160, 167–187.
Smith, B.A. et al.: 1986, “Voyager 2 in the Uranian system : Imaging science results”, Science, 233, 43–64.
Szebehely, V. : 1967, Theory of Orbits, Academic Press.
Tittermore, W.C. and Wisdom, J.: 1988, “Tidal evolution of the Uranian satellites. 1. Passage of Ariel and Umbriel through the 5 : 3 mean-motion commensurability”, Icarus, 74, 172–230.
Tittermore, W.C. and Wisdom, J.: 1989, “Tidal evolution of the Uranian satellites. II. An explanation of the anomalously high orbital inclination of Miranda”, Icarus, 78, 63–89.
Walker, G.H. and Ford, J.: 1969, “Amplitude instability and ergodic behaviour for conservative, non linear oscillator systems”, Phys. Rev., A28, 416–432.
Wisdom, J.: 1985, “A perturbative treatment of motion near the 3/1 commensurability”, Icarus, 63, 272–289.
Yoder, C.: 1973, “On the establishment and evolution of orbit-orbit resonances”, Ph.D. Dissertation, U. of California, Santa Barbara.
Yoder, C.: 1979a, “Diagrammatic theory of transition of pendulum-like systems”, Celest. Mech., 19, 3–29.
Yoder, C.: 1979b, “How tidal heating of lo drives the Galilean orbital resonance locks”, Nature, 279, 767–770.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Henrard, J., Sato, M. The origin of chaotic behaviour in the Miranda-Umbriel 3 : 1 resonances. Celestial Mech Dyn Astr 47, 391–417 (1989). https://doi.org/10.1007/BF00051013
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00051013