Abstract
The focus of the present work is directed towards the development of an effective reduced basis technique for calculating the sensitivity of the non-linear dynamic structural response of mechanical systems with respect to variations in the design variables.
The proposed methodology is formulated within the context of a mixed space-time finite element method, which naturally allows the treatment of initial and boundary value problems. The time dependency of the solutions is implied in the assumed space-time modal shapes, and hence the partial differential equations of motion are directly reduced to a set of non-linear simultaneous equations of a purely algebraic nature.
The independent field variables are approximated in terms of perturbations modes or path derivatives with respect to a load control parameter. These modes, extracting information about the kinematic and dynamic behavior of the structural system through the higher order derivatives of the strain and kinetic energies, are appropriate bases for non-linear dynamic problems. The sensitivity derivatives of the field variables are then approximated using a combination of perturbation modes and of their sensitivity derivatives.
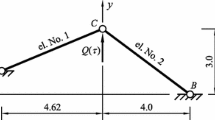
The resulting computational procedure offers high potential for the effective and numerically efficient sensitivity analysis of dynamic systems exhibiting periodic-in-time response. The proposed methodology is illustrated addressing non-linear beam problems subjected to harmonic loading and the results obtained are compared with those of a full finite-element model.
Similar content being viewed by others
Abbreviations
- (O, I i), (is1, 2, 3):
-
Inertial frame of origin O
- (P, s i), (is1, 2, 3):
-
Local frame in the undeformed configuration
- (Q, s i *), (is1, 2, 3):
-
Local frame in the deformed configuration
- t :
-
Time
- l :
-
Abscissa along the beam reference line
- L :
-
Beam length
- (·)s∂(·)/∂t :
-
Partial derivative with respect to time
- (·)′s∂(·)/∂l :
-
Partial derivative with respect to space
- u :
-
Position vector of the beam reference line
- r :
-
Rotation parameters
- ds(u, r):
-
Generalized displacement vector
- R(r) :
-
Rotation tensor associated with r
- Γ(r):
-
Tensor defined in equations (4) and (5)
- ϕsθ·κ:
-
Finite rotation vector
- as(a s, a v):
-
Conformal rotation vector
- ω:
-
Angular velocity
- ws(u, ω):
-
Generalized velocity vector
- k :
-
Curvature
- e :
-
Generalized strains
- ps(h, l):
-
Generalized momenta
- fs(s, m):
-
Generalized sectional stress resultants
- f es(S e, m e):
-
Applied external loads
- M :
-
Inertia tensor
References
Thompson, J. M. T. and Walker, A. C., ‘The nonlinear perturbation analysis of diserete structural systems’, Int. J. Solids Struet. 4, 1968, 757–768.
Noor, A. K. and Peters, J. M., ‘Reduced basis technique for nonlinear analysis of structures’, AIAA J. 18, 1980, 455–462.
Bauchau, O. A. and Guernsey, D., ‘ On the choice of appropriate bases for non-linear dynamic modal analysis’, in ‘International Technical Specialists’ Meeting on Helicopter Basic Research, Georgia Institute of Technology, Atlanta, GA, 1991.
Noor, A. K. and Peters, M., ‘Tracing post-limit-point paths with reduced basis technique’, Comp. Meth. Appl. Mech. Eng. 28, 1981, 217–240.
Noor, A. K. and Peters, M., ‘Bifurcation and post-buckling analysis of laminated composite plates via reduced basis technique’, Comp. Meth. Appl. Mech. Eng. 29, 1981, 271–295.
Noor, A. K. and Peters, J. M., ‘Reduced basis technique for calculating sensitivity coefficients of non-linear structural response’, AIAA J. 30, 1992, 1840–1847.
Bauchau, O. A. and Bottasso, C., ‘Space-time perturbation modes for non-linear dynamic analysis of beams’, to appear in Nonl. Dyn. 6, 1994.
Bauchau, O. A. and Hong, C. H., ‘Non-linear composite beam theory’, J. Appl. Mech. 110, 1988, 156–163.
Bauchau, O. A. and Hong, C. H., ‘Non-linear response and stability analysis of naturally curved and twisted beams’, AIAA J. 26, 1988, 1135–1142.
Borri, M., Ghiringhelli, G. L., Lanz, M., Mantegazza, P., and Merlini, T., ‘Dynamic response of mechanical systems by a weak Hamiltonian formulation’, Comp. & Struct. 20, 1985, 495–508.
Borri, M., Bottasso, C., and Mantegazza, P., ‘Basic features of the time finite element approach for dynamics’, Meccanica 27, 1992, 119–130.
Geradin, M. and Cardona, A., ‘Kinematics and dynamics of rigid and flexible mechanisms using finite elements and quaternion algebra’, Comp. Mech. 4, 1989, 115–135.
Noor, A. K., ‘Recent advances in reduction methods for non-linear problems’, Comp. & Struct. 13, 1981, 31–44.
Noor, A. K. and Peters, J. M., ‘Recent advances in reduction methods for instability analysis of structures’, Comp. & Struct. 16, 1983, 67–80.
Crespo da Silva, M. R. M., ‘Non-linear flexural-flexural-torsional-extensional dynamics of beams-I. Formulation’, Int. J. Solid Struct. 24, 1988, 1225–1234.
Crespo da Silva, M. R. M., ‘Non-linear flexural-flexural-torsional-extensional dynamics of beams-II. Response analysis’, Int. J. Solid Struct. 24, 1988, 1235–1242.
Crespo da Silva, M. R. M. and Glynn, C. C., ‘Non-linear flexural-flexural-torsional dynamics of inextensional beams-I. Equations of motion’, J. Struct. Mech. 6, 1978, 437–448.
Crespo da Silva, M. R. M. and Glynn, C. C., ‘Non-linear flexural-flexural-torsional dynamies of inextensional beams-II. Forced motions’, J. Struct. Mech. 6, 1978, 449–461.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Bottasso, C.L. Sensitivity analysis of the non-linear dynamic response of beams using space-time perturbation modes. Nonlinear Dyn 7, 65–84 (1995). https://doi.org/10.1007/BF00045126
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00045126