Oscillatory disturbances as admissible solutions for the flow past a cylinder and their possible relationship to the Von Karman street phenomenon

Summary

Evidently Proudman and Pearson's [1] low-Reynolds-number approximation scheme, as recently amended by the author, admits timewise oscillatory solutions. This is shown by relinquishing the implicit assumption that the flow is steady throughout, and letting instead each term in the asymptotic expansions consist of a sum of a steady component and a time-dependent one. When only one term is retained in the inner expansion, two terms in the outer and two in the recently-developed wake expansion, the solutions for the steady components are found to be determinable and equal to those recorded. However, the scheme also admits a large variety of non-trivial solutions for the time-dependent components. Attention is focused on those representing oscillatory modes of disturbance flow of indeterminable frequency and amplitude.

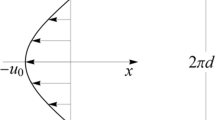
In the inner field such single mode has the form of a rotationally symmetric pattern. Far downstream it is in the form of a sequence of vorticity packets of alternate signs, equally spaced along the wake's centre plane. This pattern moves with the velocity of the undisturbed stream. The flow field resulting from such a disturbance superposed on a uniform stream bears a remarkable resemblance to the Von Karman vortex-street.