Eigenvalue analysis of size effect for cohesive crack model

Abstract

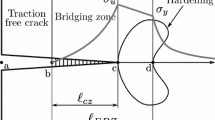
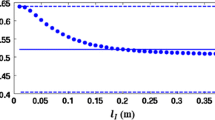
The paper analyses the effect of structure size on the nominal strength of the structure that is implied by the cohesive (or fictitious) crack model proposed for concrete by Hillerborg et al. A new method to calculate the maximum load of geometrically similar structures of different sizes without calculating the entire load-deflection curves is presented. The problem is reduced to a matrix eigenvalue problem, in which the structure size for which the maximum load occurs at the given (relative) length of the cohesive crack is obtained as the smallest eigenvalue. Subsequently, the maximum load, nominal strength and load-point displacement are calculated from the matrix equilibrium equation. The nonlinearity of the softening stress-displacement law is handled by iteration. For a linear softening law, the eigenvalue problem is linear and independent of the matrix equilibrium equation, and the peak load can then be obtained without solving the equilibrium equation. The effect of the shape of the softening law is studied, and it is found that the size effect curve is not very sensitive to it. The generalized size effect law proposed earlier by Bažant, which describes a transition between the horizontal and inclined asymptotes of strength theory and linear elastic fracture mechanics, is found to fit the numerical results very well. Finally some implications for the determination of fracture energy from the size effect tests are discussed. The results are of interest for quasibrittle materials such as concrete, rocks, sea ice and modern tough ceramics.