The cantilever strip plate under torision, bending or flexure at infinity

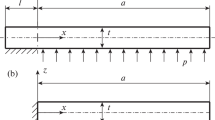
Abstract

A homogeneous, isotropic plate occupies the region 0≤x ₁≤∞, |x ₂|≤a, |x ₃|≤h, where the ratio h/a is sufficiently small so that the classical theory of thin plate bending applies. The short end of the plate at x ₁=0 is clamped while the long sides are free. This cantilever plate is now loaded at x ₁=+∞ by an applied twisting moment, by a bending moment or by flexure. Despite the fundamental nature of these problems, and the long history of thin plate theory, no solutions are to be found in the existing literature that will determine (for instance) the important unknown resultants V ₁, M ₁₁ at the clamped end x ₁=0. The main reason for this is that this combination of boundary conditions leads to severe oscillating singularities of the field in the corners (0, ±a). The fact that such singularities must exist is widely known, but we present here for the first time a method of solution that takes these singularities fully into account.

Our numerical results show that the values of M ₁₁, V ₁ on x ₁=0 bear little resemblance to those of the corresponding Saint-Venant ‘solutions’, which do not fully satisfy the boundary conditions at the clamped end. Indeed, significantly large values of these resultants were found at points far enough from the corners so as to be relevant in actual engineering applications. Also of interest are certain weighted integrals of M ₁₁, V ₁ which we calculate. These constants determine the effect of the clamping at ‘large’ distances (greater than 4a, say) from the cla,ped end. At such distances, the effect of the clamping is merely to impose an additional rigid body deflection on the plate.

Finally, we consider the plate of finite length. Provided that the aspect ratio is 2 or more, we give accurate approximate solutions for the torsion, bending or flexure of a finite plate clamped at both ends.