Abstract
Recent research in engineering seismology demonstrated that in addition to three translational seismic excitations along x, y and z axes, one should also consider rotational components about these axes when calculating design seismic loads for structures. The objective of this paper is to present the results of a seismic response numerical analysis of a mine tower (also called in the literature a headframe or a pit frame). These structures are used in deep mining on the ground surface to hoist output (e.g. copper ore or coal). The mine towers belong to the tall, slender structures, for which rocking excitations may be important. In the numerical example, a typical steel headframe 64 m high is analysed under two records of simultaneous rocking and horizontal seismic action of an induced mine shock and a natural earthquake. As a result, a complicated interaction of rocking seismic effects with horizontal excitations is observed. The contribution of the rocking component may sometimes reduce the overall seismic response, but in most cases, it substantially increases the seismic response of the analysed headframe. It is concluded that in the analysed case of the 64 m mining tower, the seismic response, including the rocking ground motion effects, may increase up to 31% (for natural earthquake ground motion) or even up to 135% (for mining-induced, rockburst seismic effects). This means that not only in the case of the design of very tall buildings or industrial chimneys but also for specific yet very common structures like mine towers, including the rotational seismic effects may play an important role.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recent earthquake engineering progress is concentrated on highly nonlinear dynamic response under extremely large earthquakes, e.g. nonlinear response of concrete [1] or steel [2] structures. The main reason for this is the constant request for structural design against catastrophic seismic events with a return period of 475 years (Eurocode 8 [3]). However, seismic engineering still has some challenges regarding the fundamental modelling of seismic loads treated as spatial types of loads, e.g. bridges [4], dams [5] or building structures [6]. These multicomponent loads may consist of not only three translational components along the x, y and z axis but also of three rotations about these axes. For a long time, the research to include rotational seismic ground motion in seismic engineering was hampered by a lack of proper ground motion instrumentation and respective rotational records. Thus, from the very beginning only indirect approaches were used. The method of body waves reflections at the free surface initially derived by Trifunac in 1982 [7], was later developed by Castellani and Boffi to generate rotational time histories [8], by Castellani and Zembaty to implement spectral approach with stochastic methodology [9] and further extended by Zembaty to include also surface waves [10]. Basu et al. proposed methods using translational records from single [11] and multiple [12] seismic stations, while Falamarz-Sheikhabadi and Ghafory-Ashtiany developed engineering methodolgy to calculate rotational acceleration response spectra from the translational ones [13]. Since the end of 90-ties of the twentieth century, more and more direct rotational seismic records were acquired, e.g. by Nigbor from an explosion [14], by Takeo from a swarm of earthquakes [15]. Zembaty et al. reported about the first rotational records from induced mining tremors (Upper Silesian Coal Basin), [16] which later served to derive 6-component Ground Motion Prediction Equations [17], while Fuławka et al. acquired the rotational seismic records from mining tremors in Lower Silesian Copper Basin [18]. Recently Bernauer et al. performed geophysical tests of various rotational sensors with active seismic sources at the Geophysical Observatory of the Ludwig-Maximilians University Munich in Fürstenfeldbruck, German [19]. The rotational records from induced seismic events allowed to compute the response of slender towers to combined horizontal-rocking seismic excitations [20]. In such the cases full seismic ground motion at a point on the ground surface can be called 6 degrees of freedom (6-dof) seismic record, as it contains three translations and three rotations.
Starting from Newmark and Rosenblueth [21], the researchers pointed out that tall buildings or slender towers may be particularly vulnerable to the rotational ground excitations about the horizontal axes. These types of ground rotations are called rocking ground excitations. Indeed, the angle of rocking as low as 1 degree at the ground surface translates into a 1.75 m at the height of 100 m [20].
Direct rotational seismic ground motion records acquired so far usually represent low or very low seismic intensities. As an example, one can mention the records of seismic signals of Modified Mercalli (MM) intensity IV, see e.g. [16] and its application to compute the seismic response of a reinforced concrete industrial chimney.
Recently, a strong MM intensity VII, 6-dof seismic record was acquired [22]. It was applied to computing the seismic response of a 160 m reinforced concrete (r/c) industrial chimney and tall buildings [23]. It was observed that combined horizontal-rocking ground motion could significantly alter the overall seismic response compared to traditional, horizontal only seismic effects. The rotational component can have both positive and negative total effect on the building structures. This analysis concluded that the rocking effects might change the seismic response of building structures up to 16%. It is still unclear, however, how the rocking seismic effects could contribute to the seismic response of other types of tall and slender structures met in civil engineering. One of such structures, which seismic response may be particularly affected by rotational components of seismic ground motion, are mine towers (headframes). This type of structure is often met in the industrial coal or copper basins of the World.
Modern mine towers are steel or reinforced concrete structures. They may reach the height of up to 87 m (steel structures) or even 132 m (reinforced concrete structures). Their purpose is to operate hoists that function mainly for vertical transport of people or output (e.g. coal or copper ore). Thus, they mainly serve to carry loads of the respective conveyances, and their primary design vertical load is their dead load and load of the hoist system. Generally, headframes can be divided onto the towers with the hoist machinery mounted inside the tower or on the ground. In the latter case one or two pairs of backlegs (inclined columns) are included in the structure of the tower. Concrete headframes can be designed without any backlegs. The most common steel headframes are structures with one pair of backlegs. Other elements of the tower are a main core, sub-beams and a structure supporting sheaves of the hoist system. The typical horizontal load of a mine tower is a wind action, seismic load and (in case of a hoist motor mounted on the ground) also load from a tension in the hoist ropes. Considering the height and cross-section of the headframes, the seismic load (natural or induced) can be more important than the wind action.
The literature on seismic effects on mine towers is rather rare. For example, there are analyses of steel mine tower by Jaskiewicz and Pytel [24], as well as concrete one by Tatara and Pachla [25]. The results of these papers reflect the conventional approach of seismic engineering, in which the seismic loads result from the action of horizontal, kinematic ground excitations. The analyses of the papers [24, 25] utilise the method of time-history response computations or the method of response spectrum. Considering the substantial height of mine towers, a question appears if the rocking component of seismic ground motion could substantially contribute to their overall seismic response. Recent results of the research in rotational seismic engineering demonstrated that the contribution of the rocking component of seismic ground motion might be important for tall buildings as was shown in simplified analyses by Sokol et al. [26] or more complex time-history analyses by Bońkowski et al. [23], and reinforced concrete industrial chimneys [20], thus it may also play an important role in the seismic response of steel mine towers.
The purpose of this analysis is to compute seismic response of a mine tower under combined horizontal-rocking excitations. These structures may be subjected to specific, near-field seismic effects from mining-induced rockbursts, e.g. [27], or in a case of mining in the areas of strong natural seismicity also from earthquakes.
2 Methodology
2.1 A mine tower as a slender structure under horizontal-rocking seismic excitations
In the present analysis seismic response of a selected mine tower subjected to conventional horizontal excitations from induced and natural earthquake are calculated. Next, the results are compared with the response including also rocking seismic effects. For this purpose, time history responses of the selected mine tower are computed for two, horizontal excitations uX(t), uY(t) and two rocking excitations Θ(t), ψ(t) acting simultaneously (Fig. 1). Two different types of seismic excitations are considered: induced seismic effects, as well as seismic records of natural earthquakes. To better compare seismic responses, the excitations are scaled to the level of intensity measured by the same horizontal Peak Ground Velocity PGVhor = 5 cm/s, which roughly corresponds to MM intensity V, see e.g. [28]. It should be also noted that PGVhor = 5 cm/s is also used as representing minimal level of intensity for induced earthquakes associated with specific minor, “cosmetic” damages of structures in areas of extensive mining [29].
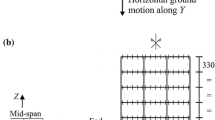
In Fig. 1. a schematic view of a mine tower situated on the ground surface is shown with two horizontal excitations N–S uX(t) and E–W uY(t) directions, including rocking excitations about these two axes. It can be seen, that for this structure the translational seismic excitations uX(t) are accompanied by respective rocking excitations ψ(t) acting in the same vertical plane, while uY(t) and Θ(t) act in the second vertical plane. As it was already shown in the papers by Bonkowski et al. [20, 23], the interaction of horizontal excitations with rocking about the axes perpendicular to the respective horizontal excitations can substantially influence overall seismic response. Thus, for these structures the horizontal seismic excitations together with respective rocking effects can be of particular importance.
The mine tower selected for the analyses of this paper is a 63.7 m high steel frame structure with two diagonal columns (backlegs) mounted to foundations at a distance of 13 m from the main steel spatial frame (see Fig. 2). At the top of the tower mechanism two pairs of sheave wheels are located. The horizontal axial dimensions of the frame equal 5.4 × 7.2 m. The multistorey steel core of the tower consists of IPE600 and C400 steel profiles and steel, welded plate girders. The backlegs of the mine tower are made from 1820 × 18 mm pipe sections.
Consider now seismic response of a mine tower modelled using Finite Element Method (FEM) and the approach of lumped masses discretized at respective FEM mesh nodes as m1, m2, …, mi, mi+1, mi+2, …, etc. The FEM model includes frame 3D elements (for details see the manual of SAP2000 [30]). A schematic view of the FEM mesh is shown in Fig. 3 in one of the two vertical planes of vibrations. It can be seen that the total seismic response consists of rigid horizontal/rocking motion of the structure and a respective elastic structural response.
The equation of motion of structure under combined, horizontal and rocking excitations in one plane is given by formula:
in which M, C, K = matrices of mass, damping and stiffness; \(\ddot{{\varvec{q}},\boldsymbol{ }}\boldsymbol{ }\dot{{\varvec{q}}}, {\varvec{q}}\) = acceleration, velocity and displacement vector at specific structural degrees of freedom; \({\varvec{m}}\) = masses of the structure in horizontal direction (product of the \({\varvec{M}}\cdot 1\), where \(1\) is the so-called influence vector filled with ones); \(\ddot{u}(t)\) = translational, horizontal ground accelerations \(\ddot{\varphi }(t)\) = rotational, rocking accelerations of the base about horizontal axis perpendicular to the axis of excitations \(u\left(t\right)\); \({\varvec{h}}\) = influence vector consisting elevations of the respective horizontal degrees of freedom above the ground surface. \(\left({\varvec{m}}{\varvec{h}}\right)\) = vector consisting of mihi values, where mi and hi stand for elements of vectors \({\varvec{m}}\) and \({\varvec{h}}\). In Eq. (1) \(\ddot{\varphi }\) stands for \(\ddot{\Theta }\) for structure excited in the Z-NS plane and for \(\ddot{\psi }\) for excitations in the Z-EW plane (Fig. 1). It should be noted that the second component of Eq. (1) reflects seismic horizontal inertial action resulting from small ground rocking (rotations about horizontal axes). For more details about equations of motion of structures under various forms of seismic excitations (spatial, torsional and rotational) the reader may refer to Anil Chopra textbook [31].
Equation (1) shows how rocking effects at the ground level translate into horizontal inertial forces proportional to the heights of the masses undergoing seismic excitations. The seismic vibrations of the mine tower analysed in this paper represent the superposition of its vibrations as excited in Z-NS and Z-EW planes (Fig. 1).
2.2 Description of seismic excitations
To investigate the role of rocking seismic effects the example mine tower is examined using four components of seismic ground motion (Fig. 1):
-
2 horizontal translations uX(t), uY(t) and
-
2 rockings Θ(t) and ψ(t)
These ground motion records are selected from two 6-dof ground motion records:
-
An induced seismic record from mine tremor recorded on 12th December 2015 in Upper Silesian Coal Basin [16] with epicentral distance 943 m.
-
An aftershock seismic record from 8th November 2014 as reported by Sbaa et al. [32] and Bonkowski el al. [33] with epicentral distance 9.2 km.
Respective acceleration response spectra are available in previous reports of one of the authors (see e.g. [34]) for mining tremor response spectrum and in publications about natural earthquake response spectra [23].
Each acceleration component \({\ddot{u}}_{x}(t)\), \({\ddot{u}}_{y}(t)\), \(\ddot{\theta }\left(t\right)\), \(\ddot{\psi }\left(t\right)\) of both records was scaled to the same moderate MM intensity ≅ V using normalising factor \(\alpha\).
where \({\mathrm{PGV}}_{\mathrm{hor}}\) is the horizontal Peak Ground Velocity according to Eq. (3):
Through this operation each scaled record has the same horizontal Peak Ground Velocity equal to 5 cm/s. The choice of PGVhor = 5 cm/s as a special benchmark intensity level was motivated by the experience of the rockburst and natural seismic effects on structures. As it was already commented the level of the PGVhor = 5 cm/s can be treated as the one bringing first structural damages, see e.g. [29]. Recent research of a big set of natural earthquake records by Worden et al. [28] attributes MM intensity V to the levels of PGV of about 4.7 cm/s and Peak Ground Acceleration (PGA) about 60 cm/s2 which is also consistent with the description of Modified Mercalli intensity V attributing this intensity as the lowest intensity causing structural damages to good quality (“healthy”) structures. The acceleration components of the rockburst record (with original PGVhor = 2.01 cm/s) were increased by multiplier 2.4649. The same scaling method applied to the Kefalonia aftershock (original PGVhor = 18.3 cm) resulted in reducing the response by a multiplier 0.2737. Scaled records of the rockburst and Kefalonia events are shown in Figs. 4 and 5 respectively.
Flowchart summarising methodology used in this research is presented in Fig. 6.
3 Results of numerical analysis
To analyse the problem a 3D FEM model of the steel mine tower has been built in SAP2000 software [30]. The model was based on the construction drawing of the existing headframe (see Fig. 2 for the schematic plan view). In the model familiar, Timoshenko beam element formulation have been utilised, which takes into account shear deformations and consist 6-dof at each node. Steel modulus of elasticity \(E=210\,\mathrm{GPa}\), Poisson’s ratio \(\nu =0.3\) and density \(\rho =7849\,\mathrm{kg}/{\mathrm{m}}^{3}\) were assumed. Influence of the technical equipment (e.g. hoist system) is considered by incorporating additional masses in the model. In the following section, the eigenproblem has been solved using eigenvector method. 16 modes are calculated to account for > 95% mass ratio. Time-history analyses are performed using modal superposition method (constant 5% damping is assumed) with 0.005 s step size.
First, a respective eigenproblem is solved. The first four natural, vibration modes are shown in Fig. 7 together with their natural periods. The 1st and 4th modes represent translational, horizontal vibrations, while the 2nd and 3rd modes stand for two, torsional vibration modes about a vertical axis.
The analysed mine tower is asymmetric in plane (see Figs. 2 and 6). Thus, it can be situated in two, perpendicular directions with respect to two pairs of ground rockings in the NS-Z, as well as EW-Z planes (Fig. 1). As an effect, the two sets of excitations of the Silesian rockburst and Kefalonia earthquake can be applied in two combinations with respect to the tower position. In what follows this is denoted as “Silesian 1”,” Silesian 2” as well as “Kefalonia 1” and “Kefalonia 2”. With this assumption, the results of this study are effectively doubled.
In Figs. 8 and 10 plots of horizontal displacements of the tower top and in Figs. 9 and 11 plots of base shear are shown with and without the contribution of the rocking seismic effects. Detailed data with all combinations of maxima for displacements, base shear and axial force in backlegs are gathered in Tables 1 and 3. In Tables 2 and 4 a relative difference in the response between the structure subjected to translational-rocking component and horizontal component only are shown. Examining Figs. 8, 9, 10 and 11 and Tables 1, 2, 3 and 4 one can conclude that the difference of seismic response for both types of loads (rockburst and natural earthquake) can be substantial. It varies between 0.1% (Base Shear in “Silesian 2” case) up to 135% (Tip displacement in “Silesian 1” case). It can be seen that for the rockburst effects the maximum absolute contribution of rocking equalled 135% while for the Kefalonia earthquake it equalled 31%. There is no simple relation in the contribution of the rocking component to different response parameters. Sometimes it is more important for displacements and sometimes for internal forces. Not in all cases, the rocking excitations contribute substantially. In some cases, there is even a reduction. This phenomenon was also reported by Bonkowski et al. [20, 23]. Whether the rotational component have positive or negative effect on the structure changes during the response (see e.g. base shear response in Fig. 11). It can be explained by the fact that maxima of horizontal and rocking excitations some time do not overlap. Overall in the case of the selected 64 m high mine tower this contribution appears to be more substantial than for the results obtained earlier for a 160 m reinforced concrete chimney [20], as well as 30-storey and ten-storey tall buildings [23].
4 Discussion
In recent years more and more six component seismic records from intensive natural earthquakes and induced seismicity are being available. The total effect of the seismic rotational component is still unknown for various types of structures. Mine towers are of special interest as they can be both subjected to natural and induced seismicity. For this purpose, a typical steel headframe is selected for the study. The analysis of seismic response of the steel mine tower was carried out for horizontal seismic excitations and for combined horizontal-rocking seismic excitations using linear time-history analyses with modal superposition method and constant 5% damping. For this purpose, two 6 component seismic records were used. One was recorded during a moderate MM intensity IV mining shock [16] and the second was acquired during a strong, MM intensity VII aftershock of natural earthquake [32]. For the convenience of the analysis both records were normalized with respect to horizontal Peak Ground Velocity 5 cm/s that is to MM intensity of about V. This resulted in base shear in range 91–164 kN and tip displacement in range 2.80–9.20 mm for induced seismicity events and base shear in range 65–124 kN and tip displacement in the range 6.64–7.95 mm for natural earthquake events. The asymmetric structure of the mine tower made it possible to compute seismic response for two cases of the situation of the tower with respect to the excitations.
As it was earlier reported for an industrial chimney [20] and tall buildings [23] the rocking excitations interact with horizontal excitations, sometime increasing, sometime decreasing the overall seismic response. For example, the inclusion of rotational component in induced seismic event decreased base shear in Y direction for 8.74% while increased tip displacements in the same direction for 135.26%, for natural earthquake there was increase of 7.26% for base shear and increase for 4.11% for tip displacements. The max contribution of rocking components reached 31% for natural seismic excitations and 135% for induced seismic effects. Such substantial difference can be probably explained by the fact, that rotational seismic effects are more pronounced very close to the epicentre which is a particular effect in the case of the recorded mine shock.
The results or rocking component contribution are in good agreement with previous studies on the effect of mining tremor on r/c industrial chimney (up to 65% contribution in bending moments at the base [20]), the effect of intensive earthquake on the 10 and 30 storey r/c buildings (e.g. up to 17% contribution in base shear [23]), or with more simplified analyses of r/c building structures (rocking contribution up to 26% [26]–43% [35]).
While the methodology of the present paper can be successfully applied for different types of structures and ground motions, one has to have in mind, that there is still deficiency of directly recorded, intensive 6-component ground motion records. Additionally, the design code [3] rotational spectra seems not be calibrated well enough [20]. This makes it much more difficult to apply rotational components in the structural design process until more 6-dof records appear. Additionally, more study on the joint ground motion and SSI effect should be done. This is especially important for vast in plane structures.
5 Conclusions
In the present research, the steel frame of the mine tower has been analysed for the effect of joint translational-rotational effects on its seismic response. Using time-history analyses, it was shown that the rotational component can significantly contribute to the dynamic response of slender asymmetric structures, such as headframes (mine towers). As shown in the previous analyses [20, 23], the rotational component can either increase or decrease the seismic response. This leads to a conclusion that the rocking component should be included not only in the design of tall towers and buildings as demonstrated in earlier papers by Bonkowski et. al [20, 23] but also for the specific type of industrial structures: mine towers which are commonly used in the deep mining infrastructure. It can be also done by applying Eurocode 8 part 6 [3] after calibrating its respective formulas with more and more analyses of seismic responses to strong motion six-component earthquakes. The higher influence of the rotational component from the induced seismicity compared to natural earthquakes leads to a conclusion that the effect of rotational component may be more pronounced for the close to epicentre events.
Availability of data and material
Kefalonia earthquake record is available on: http://dx.doi.org/10.17632/n3tgfn7xj8.1. FEM model and rockburst record is available upon e-mail request.
Code availability
Not applicable.
References
Varadharajan S, Sehgal VK, Saini B. Determination of inelastic seismic demands of RC moment resisting setback frames. Arch Civ Mech Eng. 2013. https://doi.org/10.1016/j.acme.2013.02.006.
Zhang Z, Zhang S-N, Deng E-F, Zhou T-T, Yi Y, He H, et al. Experimental study on seismic performance of double-level yielding buckling-restrained braced concrete frames. Arch Civ Mech Eng. 2020. https://doi.org/10.1007/s43452-020-00049-7.
CEN. EN 1998–1:2004 Eurocode 8: Design of structures for earthquake resistance - Part 1: General rules, seismic actions and rules for buildings. 2004.
Jankowski R, Wilde K, Fujino Y. Pounding of superstructure segments in isolated elevated bridge during earthquakes. Earthq Eng Struct Dyn. 1998. https://doi.org/10.1002/(SICI)1096-9845(199805)27:5%3c487::AID-EQE738%3e3.0.CO;2-M.
Dulińska J. In situ investigations of dynamic response of earth dam to non-uniform kinematic excitation. Arch Civ Eng. 2006;52:37–58.
Guéguen P, Astorga A. The torsional response of civil engineering structures during earthquake from an observational point of view. Sensors. 2021. https://doi.org/10.3390/s21020342.
Trifunac MD. A note on rotational components of earthquake motions on ground surface for incident body waves. Int J Soil Dyn Earthq Eng. 1982. https://doi.org/10.1016/0261-7277(82)90009-2.
Castellani A, Boffi G. Rotational components of the surface ground motion during an earthquake. Earthq Eng Struct Dyn. 1986. https://doi.org/10.1002/eqe.4290140506.
Castellani A, Zembaty Z. Stochastic modeling of seismic surface rotations. Nat Hazards. 1994. https://doi.org/10.1007/BF00643451.
Zembaty Z. Tutorial on surface rotations from wave passage effects: stochastic spectral approach. Bull Seismol Soc Am. 2009. https://doi.org/10.1785/0120080102.
Basu D, Whittaker AS, Constantinou MC. Estimating rotational components of ground motion using data recorded at a single station. J Eng Mech. 2012. https://doi.org/10.1061/(ASCE)EM.1943-7889.0000408.
Basu D, Whittaker AS, Constantinou MC. Extracting rotational components of earthquake ground motion using data recorded at multiple stations. Earthq Eng Struct Dyn. 2013. https://doi.org/10.1002/eqe.2233.
Falamarz-Sheikhabadi MR, Ghafory-Ashtiany M. Approximate formulas for rotational effects in earthquake engineering. J Seismol. 2012. https://doi.org/10.1007/s10950-012-9273-z.
Nigbor RL. Six-degree-of-freedom ground-motion measurement. Bull Seismol Soc Am. 1994;84:1665–9.
Takeo M. Ground rotational motions recorded in near-source region of earthquakes. Geophys Res Lett. 1998. https://doi.org/10.1029/98GL00511.
Zembaty Z, Mutke G, Nawrocki D, Bobra P. Rotational ground-motion records from induced seismic events. Seismol Res Lett. 2017. https://doi.org/10.1785/0220160131.
Mutke G, Lurka A, Zembaty Z. Prediction of rotational ground motion for mining-induced seismicity—case study from Upper Silesian Coal Basin, Poland. Eng Geol. 2020. https://doi.org/10.1016/j.enggeo.2020.105767.
Fuławka K, Pytel W, Pałac-Walko B. Near-field measurement of six degrees of freedom mining-induced tremors in lower Silesian Copper Basin. Sensors. 2020. https://doi.org/10.3390/s20236801.
Bernauer F, Behnen K, Wassermann J, Egdorf S, Igel H, Donner S, et al. Rotation, strain, and translation sensors performance tests with active seismic sources. Sensors. 2021. https://doi.org/10.3390/s21010264.
Bońkowski PA, Zembaty Z, Minch MY. Time history response analysis of a slender tower under translational-rocking seismic excitations. Eng Struct. 2018. https://doi.org/10.1016/j.engstruct.2017.11.042.
Newmark NM, Rosenblueth E. Fundamentals of earthquake engineering. Englewood Cliffs: Prentice-Hall; 1971.
Perron V, Hollender F, Mariscal A, Theodoulidis N, Andreou C, Bard P-Y, et al. Accelerometer, velocimeter dense-array, and rotation sensor datasets from the Sinaps@ postseismic survey (Cephalonia 2014–2015 Aftershock Sequence). Seismol Res Lett. 2018. https://doi.org/10.1785/0220170125.
Bońkowski PA, Zembaty Z, Minch MY. Engineering analysis of strong ground rocking and its effect on tall structures. Soil Dyn Earthq Eng. 2019. https://doi.org/10.1016/j.soildyn.2018.10.026.
Jaśkiewicz K, Pytel W. Shaft tower behaviour in typical seismic load conditions associated with copper ore exploitation in the foresudetic monocline. In: Potvin Y, Hudyma M, editors. Perth. Australian Centre for Geomechanics; 2005. p. 641–4.
Tatara T, Pachla F, Kuboń P. Experimental and numerical analysis of an industrial RC tower. Bull Earthq Eng. 2017. https://doi.org/10.1007/s10518-016-0053-y.
Sokol M, Ároch R, Lamperová K, Marton M, García-Sanz-Calcedo J. Parametric analysis of rotational effects in seismic design of tall structures. Appl Sci. 2021. https://doi.org/10.3390/app11020597.
Zembaty Z, Kokot S, Bozzoni F, Scandella L, Lai CG, Kuś J, et al. A system to mitigate deep mine tremor effects in the design of civil infrastructure. Int J Rock Mech Min Sci. 2015. https://doi.org/10.1016/j.ijrmms.2015.01.004.
Worden CB, Gerstenberger MC, Rhoades DA, Wald DJ. Probabilistic relationships between ground-motion parameters and modified Mercalli intensity in California. Bull Seismol Soc Am. 2012. https://doi.org/10.1785/0120110156.
Dowding CH. Construction vibrations. Upper Saddle River: Prentice Hall; 1996.
Computers and Structures, Inc. SAP2000 [Internet]. Walnut Creek, California, USA. 2019. www.csiamerica.com. Accessed 3 Feb 2020.
Chopra AK. Dynamics of structures: theory and applications to earthquake engineering. Prentice Hall: Pearson Education Limited; 2012.
Sbaa S, Hollender F, Perron V, Imtiaz A, Bard P-Y, Mariscal A, et al. Analysis of rotation sensor data from the SINAPS@ Kefalonia (Greece) post-seismic experiment—link to surface geology and wavefield characteristics. Earth Planets Space. 2017. https://doi.org/10.1186/s40623-017-0711-6.
Bońkowski P, Zembaty Z, Minch M (2018) 6-dof strong ground motion data records from Kefalonia Island (November 8th 2014, MMI = VII and November 17th 2015, MMI = V). Dataset: https://data.mendeley.com/datasets/n3tgfn7xj8/1. Accessed 3 Feb 2020.
Bońkowski PA. rotational effects for slender building structures under seismic excitations. PhD Thesis. Opole; Feb 14, 2018
Falamarz-Sheikhabadi MR. Simplified relations for the application of rotational components to seismic design codes. Eng Struct. 2014. https://doi.org/10.1016/j.engstruct.2013.10.035.
Acknowledgements
This research was partially supported by statutory funds of Polish Ministry of Science and Higher Education 007/20.
Funding
This research was partially supported by statutory funds of Polish Ministry of Science and Higher Education 007/20.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bońkowski, P.A., Kuś, J. & Zembaty, Z. Seismic rocking effects on a mine tower under induced and natural earthquakes. Archiv.Civ.Mech.Eng 21, 65 (2021). https://doi.org/10.1007/s43452-021-00221-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43452-021-00221-7