1 Introduction

1.1 Background

Geotechnical centrifuges enable the observation of movement processes in multi-phase media, such as rock and soil, deep earth materials, and alloy melts within a super-gravity environment. They also provide the primary conditions for the construction of major infrastructure, development of deep-sea resource, and research and development of high-performance materials [1,2,3,4]. The largest g-ton capacity centrifuge in at the U.S Army Engineer Research and Development Center (ERDC); it has a maximum payload of 8,000 kg at an acceleration of 143 g and 2,000 kg at an acceleration of 350 g. The maximum capacity of the centrifuge in the ERDC is 1144 gt, maximum acceleration is 350 g, radius is 7 m, and driving motor power is 1200 kW [5]. Zhejiang University and we are currently designing the CHIEF super-gravity geotechnical centrifuge, the world's largest g-ton capacity and most widely applied, multi-disciplinary super-gravity open-source experimental platform. The maximum acceleration of the CHIEF high-speed centrifuge at 1000 kg will be 1500 g, with a radius of 4.5 m and a motor power exceeding 5000 kW at atmospheric pressure. The CHIEF high-speed centrifuge will have five-fold more power and 4.3-fold more acceleration than the centrifuge in the ERDC, representing a substantial improvement in the performance of existing geotechnical centrifuges.

Temperature control and vibration balance represent the most significant challenges in the design process of CHIEF. The surface area of the heat-dissipation side wall of the CHIEF is only 60% of that of the centrifuge in the ERDC; however, its heat dissipating power is five-fold higher. Furthermore, air cooling is not permitted due to the effect of large air volumes on the vibration balance. Even when the sidewall surface is cooled with −15 ºC ethylene glycol cooling liquid, the highest simulated temperature in the cabin still exceeds 80 ºC, which is significantly higher than the 45 \(^\circ\)C limit. This defect seriously affects the accuracy and safety of the experimental data. Due to the large thermal load, limited heat dissipation conditions, and demanding temperature requirements, temperature control has become one of the critical limitations to developing this super-gravity geotechnical centrifuge. The Delft centrifuge uses a vacuum to reduce windage power and control temperature [6]. We are also considering a vacuum solution for temperature control in the CHIEF, as in other rotating machines that require temperature control such as flywheel thermal management [7]. However, the resulting pressure decrease also reduces the heat transfer coefficient. Moreover, if the reduction in the windage loss is less than that of the heat transfer coefficient, the proposed temperature control method may even increase the cabin temperature. Therefore, determining the rate of decline in the windage loss with pressure is vital for an effective temperature control design. No study has analyzed the relationship between windage loss and pressure in a geotechnical centrifuge. Therefore, in this study, we determined the influence of vacuum pumping on windage loss. Pressure drop increases the range of wake zone and turbulent kinetic energy and weakens the effect of pressure drop on reducing windage loss. Thus, windage loss presents a nonlinear relationship with pressure drop. This phenomenon is not limited to high gravity centrifuges and exists in other rotating machineries.

1.2 Literature survey

Windage loss data are essential for designing a geotechnical centrifuge [8]. Kutter et al. derived the windage loss power formula of the geotechnical centrifuge at atmospheric pressure [9]. Furthermore, they verified it on the Davis geotechnical centrifuge under the condition of acceleration below 53 g. The formula for drag torque T is as follows:

$$T = B_{C} \left( {\omega_{arm} - \omega_{air} } \right)^{2}$$
(1)
$$B_{c} = 0.5\rho_{air} \mathop \sum \limits_{i = 1}^{m} C_{di} \smallint r^{3} dA_{i}$$
(2)

where \(\omega_{arm}\) and \(\omega_{air}\) represent the angular velocity of the rotary arm and the air with the flow, respectively, \(\rho_{air}\) represents the density of air, m represents the number of components, \(C_{di}\) represents the wind resistance coefficient of i component, r represents the radius of the element, and \(A_{i}\) represents the area of the element of i component. Yu et al. extended Kutter's windage loss power equation to geotechnical centrifuge with ventilation openings [10]; Huang et al. analyzed air temperature rise using energy conservation based on this windage loss formula [11]. However, Kutter’s method is based on the assumption that the angular velocity of the internal air is the same. In practice, especially with the gradual increase in acceleration, the angular velocity of the internal air is not exactly uniform. In addition, this method depends on the determination of the wind resistance coefficient \(C_{d}\), which has to be obtained through a large number of experiments, and the \(C_{d}\) is different in different environments. Finally, when Kutter's formula is used to calculate the windage loss, the density is usually considered to be constant. However, the density of air, \(\rho_{air}\), is not constant in the direction of the radius owing to the action of centrifugal force, especially in high-acceleration cases [9]. Wang et al. developed a simplified estimation formula for the geotechnical centrifuge [12]. The final parameters have to be determined by fitting experimental data, such that the formula itself cannot reflect the influence of complex conditions, such as turbulence. Hao et al. obtained the windage loss of centrifuges via computational fluid dynamic (CFD) simulations [13]. However, due to the excessive thickness of the first boundary layer grid set in the simulations, the layer already existed in the non-viscous bottom layer, leading to errors in the calculations. Moreover, they did not evaluate the influence that the operating pressure has on the windage loss.

Motors with high-speed rotating machinery exhibit a similar temperature control problem. In contrast to geotechnical centrifuges, there has been extensive research on the thermal management of motors. Vrancik was the first to present a formula to calculate the windage loss considering turbulence [14]. According to the formula, when only the pressure changes, the windage loss is proportional to the density. In contrast, when the temperature is constant, the windage loss is proportional to the pressure. Raymond et al. summarized several standard calculation formulae for windage loss in a motor [15]. When the temperature is constant, the windage loss is also proportional to the pressure. However, windage loss simulation results and previous experimental results indicate that windage loss and pressure exhibit a nonlinear relationship [16]. In this study, we discuss the reasons for this nonlinear relationship and present arguments for its inclusion in existing windage loss formula, especially at a low pressure.

Several previous studies have confirmed the validity of the CFD method. For example, Hosain et al. used CFD simulations to obtain the velocity and temperature fields during the motor rotation process [17], successfully capturing the complex Taylor vortex. Moreover, the average surface heat transfer coefficient obtained by their simulations agrees with published data, demonstrating the effectiveness of the CFD method. Additionally, Connor et al. used CFD simulations to analyze the motor’s flow around the main parts [18]. They found that the simulated torque value is consistent with experimental data, in which the wind resistance torque accounted for approximately 87% of the total torque consumption. Furthermore, CFD simulations of a small alternator resulted in similar steady-state temperatures compared with previous experimental results [19].

Due to the lack of experimental research on vacuum windage loss, CFD simulations were employed in this study to analyze the relationship between windage loss and pressure. Therefore, this study provides a basis for the temperature control design of the geotechnical centrifuge.

2 Methodology

The radius and cabin height of the ZJU400 centrifuge at Zhejiang University are similar to those of the CHIEF design. Hence, the experimental results at atmospheric pressure can be compared and verified. In this study, we used "Fluent" software to conduct CFD simulations of the ZJU400 centrifuge and analyze the windage loss under different pressures.

2.1 ZJU400 geotechnical centrifuge

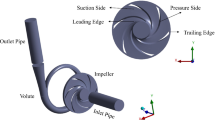
As shown in Fig. 1, the motor drives the experiment module to rotate around the axis and provide the required acceleration. With an increasing acceleration, the windage loss increases exponentially with the angular velocity, where friction heat causes a rise in the temperature. When the temperature exceeds a certain threshold, the sensor exhibits errors, such that there is a reduction in the safety of the main engine and experimental module. Therefore, effective cooling measures are required to ensure the accuracy of the experiment. Figure 2 shows a simplified model of the ZJU400 geotechnical centrifuge. The centrifuge is cooled via cooling water that flows from the top of the sidewall to the bottom, where the upper and lower walls are civil. The maximum acceleration of ZJU400 is 150 g, with a maximum operating power of approximately 200 kW. Under these operating conditions, the rise in the temperature can be controlled to within 10 ºC via water cooling along the sidewall.

Fig. 1
figure 1

Schematic of a geotechnical centrifuge

Full size image
Fig. 2
figure 2

Schematic diagram showing the a top and b side views of the computational fluid dynamics (CFD) model

Full size image

2.2 Conservation Equations using the k–ω Turbulence model

The maximum Reynolds number order of magnitude for the simulated condition is 107, which constitutes turbulent conditions. Anderson et al. and Rocha et al. used the k-ω shear-stress transport (SST) turbulence model to conduct high-speed motor and wind turbine simulations, respectively, which were verified using experimental data [20, 21]. The simulations indicate that the k-ω SST calculation model has good applicability for resolving high Reynolds number rotation problems. Therefore, in this study, we adopted the k-ω SST calculation model. The conservation equations and k-ω SST turbulence model equations solved by “Fluent” software are as follows:

Conservation of mass:

$$\frac{\partial \rho }{{\partial t}} + \nabla \left( {\rho U^{{ \sqcup }} } \right) = 0,$$
(3)

where \(\rho\) is the density and \(U^{{ \sqcup }}\) is the velocity vector.

Conservation of momentum:

$$\frac{{\partial \left( {\rho U^{{ \sqcup }} } \right)}}{{\partial t}} + \nabla \ldots \left( {\rho U^{{ \sqcup }} U^{{ \sqcup }} } \right) = - \nabla p + \mu _{{eff}} \nabla ^{2} U^{{ \sqcup }} + F$$
(4)

where \(\mu_{eff} = \mu + \mu_{t}\) is the effective kinetic viscosity, \(\mu\) is the dynamic viscosity, \(\mu_{t}\) is the eddy viscosity, and \(F\) is a miscellaneous body force term.

Conservation of momentum:

$$\frac{\partial }{\partial t}\left( {\rho E} \right) + \nabla \cdot \left[ {U^{{ \sqcup }} \left( {\rho E + p} \right)} \right] = \nabla \cdot \left[ {k_{eff} \nabla T + U^{{ \sqcup }} \cdot \tau_{eff} } \right] + S,$$
(5)

where \(E\) is the total energy, \(p\) is the static pressure, \(k_{eff} = k + k_{t}\) is the effective thermal conductivity, \(k\) is the thermal conductivity, \(k_{t}\) is the eddy thermal conductivity, \(T\) is the temperature, and \(\tau_{eff}\) is the viscous heating term, whose expression is shown in Eq. (6). The source term, S, includes the heat of the chemical reaction and any other volumetric heat sources defined by the user.

$$\tau_{eff} = \mu_{eff} \left( {\frac{{\partial u_{j} }}{{\partial x_{i} }} + \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right) = \rho v_{eff} \left( {\frac{{\partial u_{j} }}{{\partial x_{i} }} + \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right),$$
(6)

where \(v_{eff}\) = \(\mu_{eff} /\rho\) is the effective kinematic viscosity. \(\mu_{t}\) can be solved by the two k-ω SST turbulence equations, as follows:

$$\frac{{\partial \left( {\rho k} \right)}}{\partial t} + \frac{{\partial \left( {\rho ku_{i} } \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left( {{\Gamma }_{k} \frac{\partial k}{{\partial x_{j} }}} \right) + G_{k} - Y_{k} + S_{k} \;{\text{and}}$$
(7)
$$\frac{{\partial \left( {\rho \omega } \right)}}{\partial t} + \frac{{\partial \left( {\rho \omega u_{i} } \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left( {{\Gamma }_{\omega } \frac{\partial \omega }{{\partial x_{j} }}} \right) + G_{\omega } - Y_{\omega } + D_{\omega } + S_{\omega } ,$$
(8)

where \(G_{k}\) denotes the production of turbulent kinetic energy, \(G_{\omega }\) denotes the generation of ω, \({\Gamma }_{k}\) and \({\Gamma }_{\omega }\) are the effective diffusivities of k and ω, respectively, \(Y_{k}\) and \(Y_{\omega }\) denote the dissipation of k and ω, respectively, due to turbulence, \(D_{\omega }\) denotes the cross-diffusion term, and \(S_{k}\) and \(S_{\omega }\) are user-defined source terms.

$$\mu_{t} = \frac{\rho k}{\omega }\frac{1}{{{\text{max}}\left[ {\frac{1}{{\alpha^{*} }},\frac{{SF_{2} }}{{a_{1} \omega }}} \right]}},$$
(9)
$$\alpha^{*} = \alpha_{\infty }^{*} \left( {\frac{{\alpha_{0}^{*} + Re_{t} /R_{k} }}{{1 + Re_{t} /R_{k} }}} \right),\;{\text{and}}$$
(10)
$$Re_{t} = \frac{\rho k}{{\mu \omega }}.$$
(11)

where \(R_{k} = 6\), \(\alpha_{0}^{*} = \beta_{i} /3\), and \(\beta_{i} = 0.072\).

$$F_{2} = \tanh ({\Phi }_{2}^{2} )\;{\text{and}}$$
(12)
$${\Phi }_{2} = max2\left[ {\frac{\sqrt k }{{0.09\omega y^{\prime}}}\frac{500\mu }{{\rho y^{2} \omega }}} \right].$$
(13)

The default model constants for the k-ω SST model are \(\alpha_{1} = 0.31\) and \(\alpha_{\infty }^{*} = 1\). The boundary condition equation for the k-ω model applies to a low Reynolds number boundary. Thus, the first boundary layer should be in the viscous bottom layer.

2.3 Constituent parameters for the numerical model: geometry, grid, and boundary conditions

Fluent CFD software was used as the numerical simulation software [22]. A simplified CFD model was established based on the actual size of the ZJU400 geotechnical centrifuge. As shown in Fig. 2, the sidewall surface is water cooled. Considering that the thermal resistance of the water-cooled heat exchange and the thermal resistance of the wall is significantly less than that of the gas heat exchange, the temperature of the sidewall is considered to be approximately equal to that of the cooling water. In this study, we set a 293 K constant-temperature stainless-steel wall, a wall thickness of 6 mm, top and bottom wall boundary conditions for natural convection heat transfer with 300 K air, and a natural convection heat transfer coefficient of 5 W/m2 K. As friction heat causes a rise in the temperature, the viscous heat option was adopted. Based on gas compression caused by high-speed rotation, the ideal gas assumption and coupled solving method were used to solve this problem. The calculation accuracy of pressure was second order, whereas all others were third order. The roughness height of the internal wall and the rotating external wall was 0.05 mm.

Grid quality is a critical factor for the convergence of the simulation results. Concli et al. used a sliding mesh approach and multiple reference frame (MRF) model for rotating gear, showing that the MRF method exhibited a higher accuracy and required less calculations [23]. Therefore, the MRF method was adopted in this study, and the grid was structured using ICEM software. The calculation domain was divided into a rotation domain and a static domain (Fig. 3). Figure 3a shows the MRF division, such that the dark area is where the torque arm and the experiment module are located in the rotation region. Figure 3b shows the ICEM mesh topology of the rotation domain and Fig. 3c is a schematic diagram of the A–A cross-section grid (shown in Fig. 2). The boundary layer was encrypted as shown in Fig. 3d. To achieve the value corresponding to the low Reynolds number model near the wall (i.e., y +  < 15), the node height of the first layer of the grid near the wall of the rotating body and the inner wall was set to 0.05 mm. Figure 3e is the grid independence test result, where the ordinate value is the normalized processing result based on the windage loss power when the number of grids is 4.96 × 107, and the number in “mm” is the thickness of the first layer of grids. As shown in the figure, when the number of grids is greater than 4.96 × 107, the windage loss power results are grid independent and the continuous decrease in the thickness of the first layer grid from 0.05 mm does not affect the calculation results. After the grid-independent test (Fig. 3e), the final grid quantity was 4.96 × 107. The grid was a structured grid, with a minimum grid quality of 0.37 calculated using Fluent. If an unstructured grid is adopted, when the boundary layer is densified to 0.05 mm at the node height corresponding to the first layer under tens of millions of grids, there is a significant reduction in the grid quality, and the calculation cannot be convergent. Therefore, to obtain a structured grid with good grid quality, geometric approximation processing was performed at the chamfering angles of the experimental module and the rotating arm.

Fig. 3
figure 3

a Multiple reference frame (MRF) division diagram; b ICEM topology diagram of the rotating domain; c schematic diagram of the ICEM A–A cross-section grid; d schematic diagram of the ICEM boundary layer grid; and e grid independence results

Full size image

Figure 4 shows the simulation flow chart of ZJU400. The first level includes the major steps and the second level includes the parameters and settings that should be considered in Ansys Fluent for the corresponding steps. As Fluent mainly uses the finite volume method (FVM) to perform simulation calculations, the mesh division steps need to be undertaken more carefully. In particular, the thickness of the first boundary layer, the number of meshes, whether the mesh is unstructured, and the quality of mesh need to be considered as all of these affect the outcome [22].

Fig. 4
figure 4

Flow chart of simulation

Full size image

3 Results and discussion

3.1 Experimental verification of CFD simulation at atmospheric pressure

Figure 5 shows the CFD streamline diagram and velocity vector diagram of ZJU400. The fluid streamlines in most regions exhibit a regular circular motion. At the same time, those in the vicinity of the contact area between the experimental cabin and air are disordered (Fig. 5a), which is mainly due to the push wave and wake flow caused by air rotating around the cabin. The velocity vectors reveal that the fluid rotates counterclockwise, identical to the swirl direction (Fig. 5b).

Fig. 5
figure 5

a Streamline diagram at an acceleration of 120 g and b velocity vector diagram at an acceleration of 120 g

Full size image

Figure 6a is the pressure nephogram of the center plane of the tumbler and the streamlines of particles relative to the rotating arm. The rotating arm moves counterclockwise, and the solid black line is the streamlines of particles relative to the rotating arm, which can better reflect the flow movement before and after the tumbler. On the windward side of the rotary arm, the air particles are compressed and accelerated, and the centrifugal force increases at the same time. Under the joint action of thrust and the centrifugal force, the particles move radially from the inside to the outside, as shown with arrow 1 in Fig. 6a. The pressure increases in the clearance area of the front end of the rotary arm due to the radial movement of particles squeezing into it. Particles travel from the windward side to the leeward side of the tumbler through the clearance at the end of the tumbler. Conversely, particles on the leeward side of the tumbler reduce their velocity and centrifugal force due to the viscous resistance in the boundary layer. In contrast, due to backpressure, the radial pressure difference increases. When the radial pressure is greater than the centrifugal force, the particle moves in the radial direction from the outside to the inside, as shown with arrow 2 in Fig. 6a. In the backpressure area, vortex shedding occurs. At this time, particles will leave the back of the rotary arm along with vortex shedding, as shown with arrow 3 in Fig. 6a. When the inertial flow (shown with arrow 4 in Fig. 6a) enters the windward side of the other side of the rotary arm, it forms a period. There was a radial movement of particles from the inside to the outside in the windward side and from the outside to the inside on the leeward side. Figure 6b shows the turbulent kinetic energy nephogram of the center plane of the tumbler and the streamlines of particles relative to the rotating arm. Turbulent kinetic energy is the product of turbulence velocity fluctuation variance and fluid mass, reflecting the turbulence strength. The region with a large turbulent kinetic energy occurs in the wake area of the rotary arm, which could be caused by vortex shedding generated in the wake area according to the streamlines.

Fig. 6
figure 6

a Pressure nephogram and the streamlines of particles relative to the rotating arm and b turbulent kinetic energy nephogram and the streamlines of particles relative to the rotating arm

Full size image

Figure 7 is the CFD temperature cloud diagram for the A–A cross-section at 120 g. When the windage loss is 144.2 kW, the sidewall water-cooled temperature control method has a good effect. The high-temperature zone is at the end of the arm and middle area, where the maximum rise in the temperature is only 8 K. The outer end of the arm is hot because it generates the most friction heat, while the middle part is hot because it is the hardest location from which heat can dissipate. We measured a rise in temperature at the center of the cabin of 7.7 K, consistent with the simulation results.

Fig. 7
figure 7

Temperature cloud image of the A–A cross-section at an acceleration of 120 g

Full size image

Figure 8 shows a comparison between the measured ZJU400 motor power and CFD simulation windage loss at different accelerations under normal pressure. The black rectangular point in Fig. 8 is the windage loss obtained from the CFD simulation, the red circle is the measured motor power, the red curve is the formula fitting curve based on the simulation results (i.e., the fitting formula in Eq. (17)), and the dotted line is the deviation curve of the relative fitting curve. When the speed is less than 10 rad/s, the deviation between the fitting curve and measured motor power is approximately 35%. However, the deviation decreases to 15% when the angular speed is more than 14 rad/s.

Fig. 8
figure 8

Measured motor power and CFD windage loss

Full size image

Table 1 shows a comparison of the simulation results and experimental data. The first column is acceleration, the second is the measured motor power, the third is CFD simulation windage loss power, and the fourth column is the deviation value of the simulated windage loss power based on the experimental motor power. It should be noted that the deviation value in Fig. 8 is the deviation value of the experimental motor power based on the fitting curve, and the numerical significance of the deviation in column 4 is different from that in Table 1. As the windage loss power is equal to the motor power minus the motor efficiency loss and the bearing friction loss, we need to consider the influence of motor power loss and bearing friction loss. The following is a brief discussion on the estimation of these two losses. The motor efficiency of ZJU400 is approximately 90%, according to the data provided by the motor manufacturer. Bearing friction loss power is difficult to measure on the existing experimental platform of ZJU400; therefore, we made a prediction based on available data. The prediction is based on the following two preconditions: (1) the deviation between the simulated windage loss power and the actual wind resistance power is between -30% and + 15% and (2) the friction power of bearings has an exponential relationship with angular velocity, where the exponential is 1.5. The numerical deviation in column 4 indicate that the deviation values of simulated windage loss power and motor power are both stable between -28.7% and -7.8%; therefore, we believe that premise 1 is reasonable. Premise 2 refers to the calculation of bearing friction power by Calasan [24]. Therefore, it can be inferred that the bearing friction power range at 10 g is 0–1.95 kW (bearing friction power = motor power × motor efficiency—simulated windage loss power/(1.15–0.7)). According to the 1.5 exponential relationship between bearing friction power and angular velocity, the speculated range of bearing friction power can be obtained, as shown in column 5 in Table 1. Column 6 in Table 1 shows the error ratio between the simulated windage loss power and the motor power minus motor efficiency loss and bearing friction power loss. When motor efficiency loss and bearing friction power loss were considered, the positive deviation of simulated windage loss power was not more than + 15%. The maximum negative deviation is -20.7% when the negative deviation is 10 g. The trend and values of the simulated windage loss agree well with the measured data, confirming the validity of the simulation results. These results indicate that the CFD model produces good simulation results for ZJU400, such that the model can be used to analyze windage loss under different pressures.

Table 1 Comparison of simulation results and experimental data
Full size table

3.2 Correlation between windage loss and pressure

CFD simulations were conducted under operating pressures of 5000, 10,000, 20,000, 50,000, and 101,325 Pa (atmospheric pressure) and under acceleration conditions of 30, 60, 90, and 120 g. Figure 9 shows the variations in windage loss with acceleration under different operating pressures. Compared to the vacuum condition, atmospheric pressure results in a greater increase in the windage loss with centrifugal acceleration. When the pressure drops to 5000 Pa at a centrifugal acceleration of 120 g, the windage loss considerably decreases from 144.2 to 10.0 kW. At a high centrifugal acceleration, the windage loss can be significantly reduced by lowering the pressure. For example, for the 1,500-g high-speed centrifuge CHIEF project under construction in Zhejiang University, the windage loss can be reduced to the megawatt level via vacuum pumping. Thus, reducing the pressure is an appropriate means to control the heating power of the geotechnical centrifuge.

Fig. 9
figure 9

Relationship between the windage loss and centrifugal acceleration under different operating pressures

Full size image

Figure 10 shows the variations in windage loss with pressure under different accelerations, with the corresponding fitting formulae listed in Table 2. These results confirm that the windage loss is not linear, with an increase in the pressure. At different centrifugal accelerations, the exponential value of the pressure is approximately 0.88 with no significance. The change indicates that centrifugal acceleration does not significantly affect the nonlinear relationship between windage loss and pressure.

Fig. 10
figure 10

Relationship between windage loss and operating pressure under different centrifugal accelerations

Full size image
Table 2 Fitting formulae for windage loss and operating pressure under different centrifugal accelerations
Full size table

3.3 Viscous heat and nonlinear relation between windage loss and pressure

Available windage loss formulae describe a linear relationship between windage loss and pressure. Therefore, we discuss the reasons for the observed nonlinear behavior. The second term on the right of Eq. (5) is the viscous heat correlation term. Combined with Eq. 6, viscous heat is predominantly related to velocity distribution, density, and effective kinematic viscosity. As windage loss should be converted to viscous heat under stable conditions, examining the viscous heating term is equivalent to investigating the windage loss. The results under 5000 Pa and atmospheric pressure were compared and analyzed to determine the influence of velocity distribution and effective kinematic viscosity on windage loss under different pressures. For simplicity, only the results at an acceleration of 90 g are shown, as the results for all other acceleration conditions were similar.

3.4 Results of velocity versus pressure

Figure 11a, b shows the A–A cross-section velocity cloud maps at 5,000 Pa and atmospheric pressure, respectively, revealing maximum cross-section velocities of 81.7 and 77.5 m/s, respectively. The maximum change in the velocity was only 5%, with overall similar velocity distributions. To more clearly observe the velocity differences, Fig. 11c, d shows a comparison of the velocity between lines one and two (see Fig. 2a for the positions of lines one and two). The velocity differences for lines 1 and 2 were < 5% and < 3%, respectively. Therefore, we suggest to ignore the change in viscous heat caused by the change in velocity under different pressures.

Fig. 11
figure 11

Velocity cloud image of the A–A cross-section at a 5,000 Pa and b atmospheric pressure. Lines c one and d two velocity comparison diagrams

Full size image

3.4.1 Effective dynamic viscosity versus pressure

Figure 12 shows cloud images of the effective dynamic viscosity in the A–A cross-section at 5000 Pa and atmospheric pressure. When the pressure drops from atmospheric pressure to 5000 Pa, the maximum effective dynamic viscosity decreases from 0.29 to 0.015, representing a decrease of 94.8%. This drop is mainly due to a 95% reduction in density. Therefore, we can ignore the change in the spatial distribution of the velocity with pressure. Thus, according to Eq. (6), the windage loss is only related to the effective dynamic viscosity. The significant decrease in the maximum effective dynamic viscosity is why windage loss decreases with reduced pressure. However, Fig. 12 also shows that low pressure leads to a significant increase in the wake area, which increases the mean value of the effective dynamic viscosity and enhances the reduction in the windage loss with decreasing pressure.

Fig. 12
figure 12

Effective dynamic cloud image of the A–A cross-section at a 5000 Pa and b atmospheric pressure

Full size image

3.4.2 Effective kinematic viscosity versus pressure

The effective dynamic viscosity is the product of density and effective kinematic viscosity. We analyzed the effective kinematic viscosity separately to remove the influence of density. Figure 13 presents comparison charts of the effective kinematic viscosity for lines 1 and 2 at 5,000 Pa and atmospheric pressure. If the effective kinematic viscosity does not change with the pressure, then the viscous heating term (i.e., the windage loss) has a linear relationship with density (pressure) when only the pressure condition changes (Eq. (6), whose results match the simplified windage loss formula listed in Table 3 (15). However, Fig. 13 shows that the maximum effective kinematic viscosity for lines 1 and 2 at 5,000 Pa increases by approximately 60% and 40%, respectively, under atmospheric pressure. Therefore, the assumption that the effective kinematic viscosity does not change with pressure is not valid. An increase in the effective kinematic viscosity increases the viscous heating term (i.e., the windage loss), resulting in a nonlinear relationship between the windage loss and density (pressure). Therefore, the main reason that the simulated windage loss power is nonlinear with pressure is because the effective kinematic viscosity increases with the decrease in pressure.

Fig. 13
figure 13

Effective kinematic viscosity comparison diagram for lines a one and b two

Full size image
Table 3 Available calculation formulae for windage loss
Full size table

To understand the cause of this change in the effective kinematic viscosity with pressure, we employed the following definition of effective kinematic viscosity:

$$v_{eff} = v + \varepsilon_{M} ,$$
(14)

where \(v\) is the kinematic viscosity and \(\varepsilon_{M}\) is the eddy diffusion coefficient. As the kinematic viscosity changes, \(v\) with pressure can be ignored [25], only the eddy diffusion coefficient is considered. The formula for \(\varepsilon_{M}\) is as follows:

$$- \overline{u^{\prime}v^{\prime}} = \varepsilon_{M} \frac{{\partial \overline{u}}}{\partial y},$$
(15)

where \(u^{\prime}\) and \(v^{\prime}\) are the velocity pulsation components in the x and y directions, respectively, and \(\overline{u}\) is the mean velocity during turbulence. Pressure has little influence on the time-averaged velocity, such that the eddy viscosity \(\varepsilon_{M}\) is related to the velocity pulsation component.

Turbulent kinetic energy is the square of the velocity pulsation component and can reflect the magnitude of the velocity pulse. Figure 14 presents turbulent kinetic energy cloud images of the A–A cross-section at 5000 Pa and atmospheric pressure. At 5000 Pa, both wake area and turbulent kinetic energy are larger, nearly twice the values at atmospheric pressure. Therefore, a reduction in the pressure increases the velocity pulsation component and wake area. These changes yield an increase in the eddy diffusion coefficient, \(\varepsilon_{M} ,\) and the effective kinematic viscosity.

Fig. 14
figure 14

Cloud diagram of the turbulent kinetic energy at a 5000 Pa and b atmospheric pressure

Full size image

In summary, the pressure drop has a minimal effect on the spatial distribution of velocity, whereas the effective kinematic viscosity has a substantial effect. An increase in the wake area and an increase in the turbulent kinetic energy within the wake area are the major causes of the increase in the effective kinematic viscosity with reduced pressure, which is also the reason for the nonlinear relationship between the windage loss and pressure. We can extrapolate that a larger wake vortex of the rotating body will result in a more nonlinear windage loss with pressure.

3.5 Comparison of simulated and calculated values of windage loss

Table 3 lists the theoretical expressions of windage loss for a motor (15), where L is the rotor length and R is the rotor radius. Wang et al. developed a highly accurate empirical formula for the windage loss of geotechnical centrifuge [12], as shown in Eq. (16), where \(C\) and \(n\) are the constants obtained by fitting with experimental data:

$$P_{w} = C\rho \omega^{n} .$$
(16)

Equation (16) is similar to the expression of windage loss listed in Table 3, which indicates that windage loss is proportional to density. Therefore, Eq. (16) was used to fit the simulated windage losses shown in Fig. 8. The fitting results can be expressed by Eq. (17), with a correlation coefficient (R2) of 0.996. The fitting formula exhibits good agreement under atmospheric pressure and conforms to the expression in Table 3. As shown in Fig. 8, the simulated windage loss is consistent with the curve in Eq. (17) under atmospheric pressure conditions:

$$P_{w} = 19.84\rho \omega^{3.11} .$$
(17)

However, when the pressure is reduced, both Eq. (16) and the simplified windage loss expression in Table 3 indicate that windage loss has a linear relationship with density (pressure). Therefore, the results are not consistent with the nonlinear results obtained from our simulations, as well as the experimental results reported by Cao et al. [16].

Figure 15 shows a comparison of the simulated CFD windage loss and the windage loss calculated according to Eq. (17) at 120 g. The simulated windage losses at 20,000, 10,000, and 5,000 Pa were 20.6%, 32.5%, and 40.2%, respectively, higher than those calculated using Eq. (17). The relative deviation increases with a reduction in the operating pressure. Therefore, although Eq. (17) accurately reflects the actual windage loss at atmospheric pressure, the windage loss calculated under a high degree of vacuum is underestimated. This error is enhanced when the heat transfer coefficient also decreases rapidly with the pressure, which seriously affects the temperature control design of the super-gravity geotechnical centrifuge.

Fig. 15
figure 15

Comparison of the simulated CFD windage losses and those calculated with the fitting formula

Full size image

Vrancik first proposed a windage loss formula for a motor that considers the influence of turbulence [14], which can be expressed as the Reynolds number (\(R_{e} = ud/v\)). The Reynolds number is used to reflect the influence of turbulence; this method has been widely used to calculate the turbulence. The windage loss formula in Table 3 reflects the viscosity effect due to the kinematic viscosity, which can also be expressed as the Reynolds number. As the pressure has negligible influence on the velocity and kinematic viscosity [25], the Reynolds number does not change with pressure. Therefore, the Reynolds number cannot reflect the pressure on the turbulence state, that is, the linear relationship between windage loss and density neglects the effect that pressure has on turbulence. There are situations where a low pressure leads to increased turbulence, such as the instability situation for low pressure rotating flow in turbines [26]. In the CFD calculation, the effective kinematic viscosity (defined as Eq. (14)) is used to replace the kinematic viscosity and consider the effect of the eddy diffusion coefficient, as well as the change in the kinematic viscosity, which more comprehensively reflects the influence that turbulence has on windage loss.

3.6 Modified windage loss expression with pressure effects considered

To consider the effect that pressure has on the turbulence conditions, we modified Eq. (16) as follows:

$$P_{w} = \alpha \cdot C \cdot \rho \omega^{n} .$$
(18)

\(C\) and \(n\) can be obtained using Eq. (16), which can be derived by fitting the data at atmospheric pressure. Here, \(\alpha\) is the pressure correction coefficient. According to a comparison between the CFD simulation results and Eq. (17) under different operating conditions, Fig. 16 shows the pressure correction coefficient. The R2 of the fitting curve is 0.977, which indicates a reasonable degree of fit.

Fig. 16
figure 16

Pressure correction coefficient diagram

Full size image

The fitting curve shown in Fig. 16 has the following form:

$$\alpha = A \cdot e^{ - p/B} + D,$$
(19)

where \(A\), \(B\), and \(D\) are constants, and \(p\) is the pressure value. Therefore, the modified fitting formula considering the influence of pressure can be expressed as follows:

$$P_{W} = \left( {Ae^{ - p/B} + D} \right) \cdot C \cdot \rho \omega^{n} .$$
(20)

For the ZJU400 operating conditions applied in this study, the final modified windage loss expression, after considering the influence of pressure, is as follows:

$$P_{W} = \left( {0.619e^{{ - \frac{p}{18268}}} + 1.009} \right) \cdot 19.84 \cdot \rho \omega^{3.11} .$$
(21)

Compared with Eq. (16) and Table 3, Eq. (20) considers that increased turbulence in the wake area, caused by decreasing pressure, affects the windage loss. Therefore, Eq. (20) can be used as a reference to predict the windage loss at a low pressure for rotating machinery with a wake flow. Stronger wake flows result in more nonlinear pressures, as well as smaller B values.

3.7 Advantages and limitations of the CFD simulation method

CFD simulations of the turbulence problems are well developed and highly accurate. Moreover, the CFD method can provide physical quantities that are difficult to measure but directly affect the windage loss, such as the effective kinematic viscosity and spatial distribution of the velocity. By comparing and analyzing the CFD results of these parameters under different operating pressures, the influence of the operating pressure can be determined, which can help understand and predict the influence that the operating pressure has on windage loss.

For the geotechnical centrifuges with complex shapes, it is difficult to divide structured grids, leading to poor grid quality. Precisely, when the thickness of the first layer boundary layer grid cannot conform to the requirements of the calculation model, the CFD results may deviate substantially, leading to incorrect conclusions. In this study, the ZJU400 centrifuge was examined in a pressure and acceleration range of 5,000–101,325 Pa and 30–120 g, respectively. However, the actual values may vary beyond this range, especially when an increase in the angular velocity leads to a sharp rise in the temperature. Therefore, the influences that temperature changes have on the density, effective kinematic viscosity, and spatial distribution of the velocity in Eq. (6) should be considered for these conditions.

4 Conclusions

The geotechnical centrifuge is essential for applications such as soil mechanics research, geotechnical centrifugal simulation tests, and high-performance material research and development. Consequently, determining the decline in the windage loss rate with pressure is vital to ensure an effective temperature control design for future super-gravity geotechnical centrifuges. In this study, a model of the ZJU400 centrifuge was simulated to analyze the relationship between windage loss and pressure. The simulated windage loss and temperature deviation from the experimental data was < 20.7% at atmospheric pressure, confirming the reliability of the CFD method. The results reveal a nonlinear relationship between windage loss and pressure. Pressure drop had negligible influence on velocity distribution, whereas effective kinematic viscosity substantially influenced the velocity distribution. This is predominantly because the pressure drop increases the wake area range and turbulent kinetic energy, consequently increasing the overall turbulence and weakening the effect of the drop in pressure on windage loss reduction.

The windage loss results simulated by the CFD at 5,000 Pa were 40% larger than that calculated with Eq. (17). This difference will seriously affect the temperature control design when the heat transfer performance also experiences a rapid decline. This difference is that the Reynolds number in Eq. (17), which reflects turbulence in the windage loss calculation, cannot reflect the influence of pressure on turbulence, whereas this is possible in the CFD simulation. Furthermore, a modified windage loss fitting formula that considers the influence that pressure has on turbulence was proposed, which provides a basis for predicting the windage loss of vacuum pumping. The windage loss formula can also serve as a reference for other rotating machinery exhibiting wake flow.

Methods to reduce the windage loss power of the geotechnical centrifuge will be studied in the future. For example, the aerodynamics of the geo-centrifuge will be improved, including setting a fairing before and after the experimental chamber, optimizing the shape of the fairing, and optimizing the size of the geotechnical centrifuge. Furthermore, research on meshing will be carried out to obtain high-quality structured meshing for complex shapes. In addition, the influence of different substances on windage loss power will also be studied, for example, the density, viscosity, and other physical properties of helium gas can theoretically result in a substantial reduction in the windage loss in order to conform to the temperature control requirements.