1 Introduction

In radiation dosimetry, it is sometimes difficult to avoid the theoretical calculation for the absorbed dose. However, the accuracy of the estimated dose is always required. Therefore, theoretical methods such as the Monte Carlo (e.g. [8, 25]), have been used in numerous applications. However, the using of the Monte Carlo algorithm in radiation dosimetry requires a fully computational design for the experimental system including the geometrical properties of the radiation source, the geometrical properties of the irradiator facility, considering all the possible physical interactions of the radiation particles with the surrounding medium, and having the required library for the interaction cross-section information [55]. Thereby, the complexity and difficulties of using this method restrict its use especially in the routine work [60]. On the other hand, the artificial neural network (ANN) is an intelligence method that is based on establishing a connection between the input and the output data for nonlinear system without the necessity to know how the system works internally [26]. Therefore, the ANN can lead to much lower computational time [53].

The interpolation fitting algorithms have been widely used in the field of radiation dosimetry. Baltas et al. [4] recommended a simple liner interpolation fitting. On the other hand, others [19, 33] argued that the cubic spline interpolation method is more accurate than the linear interpolation method. Nevertheless, the simplicity of the linear interpolation fitting method is always a point of strength [39]. In fact, the interpolation methods in most cases are limited to estimate the data within the measured values. Therefore, Baltas et al. [4] advised that special care shall be taken into accounting for evaluating the dose rate values for positions outside the range of the original data.

The artificial neural network (ANN) modeling technique aims to find a relationship between the input and the target. This technique has been applied to predict the output response of certain system e.g. [1, 20, 42, 54, 57]. A comparison between the ANN and the regression models has been also investigated [30]. However, there is a different between the two techniques. The ANN does not produce a mathematical expression that related the input to the output, but rather a black-box of numerous mathematical processes that attempt to capture the way the output changes with changing the input [9, 31]. Thus, ANN model consists of connected input layers, hidden layer(s) and output layer. The dimension of each layer is described by the number of neurons nodes. The connection strength between the nodes is modeled as synaptic weight. The main idea of the ANN modeling technique is to adjust the values of the synaptic weight so that the error of the network output (i.e. the deviation of the output from the target) is minimized [23]. The optimization process is established based on certain “learning rules”.

The back-propagation (BP) learning rules have shown a quite robust algorithm to minimize the error function [34]. In this algorithm, the learning process is conducted on two sequential processes. In the first process (called forward process), the error in the network output is computed using initial values of the synaptic weight. The initial values are being selected using certain random-based initialization function. The second process is the “backward pass” in which the error of the output is passed backward to the network to adjust and update the synaptic weight values so that the error of the network output is minimized.

The ANN modelling algorithm has been used to evaluate the dose distribution and the dose uniformity in the Tunisian gamma irradiator [37] where the measurements were carried out using polymethyl methacrylate dosimeters. However, the ionization chamber dosimetric system is a benchmark of dosimeter, and had been known to provide the most accurate and reliable results [41]. Therefore, in the current work, the ionization chamber system has been used to measure the radiation dose-rate. The aim of the current work is to:

  1. 1.

    Build a black-box model using the ANN algorithm to simulate the response of an ionization chamber system in measuring the radiation dose-rate of 137Cs.

  2. 2.

    Compare between the accuracy of the ANN algorithm and the accuracy other usual interpolation methods.

2 Experimental data

The dose rate of 137Cs irradiator manufactured by Atomic Energy of Canada LTD (Model No. G.B. 150) was experimentally measured using the secondary standard dosimetry system of the National Institute for Standards (NIS)—Egypt. The dosimetry system consists of TM-30013 ionization chamber manufactured by PTW and calibrated at the International Atomic Energy Agency (IAEA). The ionization-chamber is connected to PTW electrometer calibrated at the Bureau International des Poids et Mesure (BIPM).

The dose-rate was recorded for different positions from the radiation source using the ionization-chamber system. Each position is designated by x–y coordinates as illustrated in Fig. 1. The replicate number of each dose-rate measured by the ionization chamber is 10.

Fig. 1
figure 1

Schematic representation describing the x–y coordinates of the ionization chamber from the radiation source

Full size image

The radiation dose-rate was recorded at 190 different positions. The dose-rates at 146 different positions have been used to build-up the computational model (data for training) and the dose rates measured at the other 25 positions have been used to examine the accuracy of the model (data for validating). The data used in the validation process were randomly selected to cover the whole range of the experimental results as illustrated in Fig. 2.

Fig. 2
figure 2

Selection of the data used in validation process to cover the range of the experimental results

Full size image

3 Computational algorithms

3.1 Classical interpolation methods

In the current section, the curve interpolation methods using linear, cubic spline, nearest-neighbor and thin-plate spline algorithms have been used to fit the experimental data. The fitting results are presented in Fig. 3.

Fig. 3
figure 3

Interpolation fitting using linear, cubic-spline, nearest-neighbor and thin-plate algorithms for the experimental data results obtained using ionization chamber system

Full size image

It is obvious from the figure that the interpolation fitting using “linear” and “cubic-spline” can only fit the data points the lie within experimental results. In the “nearest-neighbor”, no new data points are generated, the method sets the fitted value to the neatest experimental value. However, it is obvious that the interpolation fitting using “thin-plate” method could fit all the experimental data.

3.2 Artificial neural network (ANN) model

3.2.1 Assigning the functions and the parameters of the ANN

The processes functions and parameters of the ANN are dependent on the nature of the problem [44]. Hence, there is no universal design for the ANN that is applicable for any (or even a certain) type of experimental data [49]. Consequently, approaching the optimum design for the ANN is mainly a trial and error procedure [45] and also on the examples and experiences provided by the user [53]. Thus, the optimum design for the ANN can be proposed by varying the number of hidden layers, transfer function and the number of neurons in each hidden layer [17, 56]. The efficiency of the ANN can be validated throughout several validation methods. Most of these methods aim to assess the difference between the ANN output and the experimental results, i.e. the error function. The linear regression analysis is one of the efficient methods that can measure the performance of the network [48]. However, monitoring the performance of the ANN during the learning processes is also a crucial factor [44]. These subjects have been discussed in details in Sects. 4.1 and 4.2.

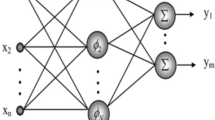
In order to approach the optimum ANN design, the performance of the network has been examined for different neurons number and hidden layers. Furthermore, the performance of the network has been monitored for different processes functions and wide range of parameters in such that a generalized optimum performance of the ANN is approached with the simplest design [7]. It has been found that the optimum performance of the ANN has been approached with three hidden layers and a total number of 80 neurons. The processes functions and parameters of each layer is illustrated in Table 1. A graphical representation for the design of the ANN is presented in Fig. 4.

Table 1 Input functions and parameters used in the designed ANN shown in Fig. 4
Full size table
Fig. 4
figure 4

Architecture representation for the final design of the artificial neural network used in the current work

Full size image

3.2.2 Input, target and output data

The learning process in ANN is performed mainly throughout two stages. In the first stage, the ANN trains on how the input is correlated with the output. While, in the second stage the ANN validates the generality of the training process. Therefore, the experimental data are divided into two groups; one group for the training stage and one group for the validation stage. It is common to divide the data into 70% and 30% for the training and the validation processes, respectively [59]. The validating data are used by the network to ensure the generality of the network and preventing from falling into a local optimum [22]. However, occasionally, the 30% of the data is further divided into 15% for validation and 15% for testing. The testing process examines the performance of the network for new different data, i.e. data were not included in the training process.

In the current work, the input of the ANN is the x–y position coordinates (in cm) of the ionization chamber with respect to the radiation source. While, the output is the dose rate in mGy/h. The input and output data have been transformed into scaled-range data before the ANN uses them in the training stage. Indeed, using scaled-range data significantly improves the performance of the ANN [2]. The transfer functions used in the current work have been further discussed in Sect. 3.2.5.

3.2.3 Hidden layers and neurons size

The design of any ANN consists of one input layer, one or several hidden layers, and one output layer. For each layer, the dimension of the layer (number of neurons), initial function, net input function and the transfer function should be assigned by the user in accordance with the general criteria discussed in Sect. 3.2.1.

In multiple hidden-layer ANNs, each layer applies different process function on the output of the previous layer [44]. Thus, the output of the first hidden layer is the input of the second hidden layer. Usually, a NNN with two hidden layers can approach the optimum performance [3]. However, in the current work, the optimum design has been reached with three hidden layers. In order to determine the neurons number in each hidden layer, the performance of the network has been monitored over different layers’ sizes. The following procedure has been followed:

  1. 1.

    More than 30 different designs for the ANN have been set up. In each design, the dimensions of the three hidden layers have been randomly selected from a specified range of [2, 50].

  2. 2.

    For each design, the weights and biases values have been reinitiated to ensure the generality of the learning process.

  3. 3.

    Step no. 2 has been repeated 10 times for each design and the minimum mean square error \(\left( {mse} \right)\) has been evaluated.

  4. 4.

    The mean value of the \(mse\) and its standard uncertainty \(u\left( {mse} \right)\) have been monitored over the different designs of the ANN. The results are presented in Fig. 5.

Fig. 5
figure 5

Performance of different ANN designs over different neurons sizes distributed randomly over three hidden layers

Full size image

It is obvious from the figure that the optimum performance of the network can approach \(mse < \sim 1\) with a total number of 80 neurons distributed over the three hidden layers. It was reported that the number of neurons should not be unnecessarily large or unnecessarily small to avoid the overfitting or the lack fitting, respectively [7, 61]. It is obvious from the figure that increasing the neurons size more than 80 does not significantly improve the performance of the network. On the other hand, it significantly increases the computational time required for convergence. It is worthwhile to mention that it is not necessarily the neurons should be equally distributed over the three hidden layers. However, the total number of the neurons in the three hidden layers should not be < 80.

The optimal weights and biases are obtained by training the ANN so that the error between the ANN output and the target is minimized. Therefore, unrealistic small or high weight values influence the performance of the network. Therefore, substantial improvements have been established to develop a method for selecting the appropriate initial values for the weights and biases that prevent the network for being stuck into a local minima. In the current work, the Nguyen–Widrow algorithm [43] has been applied. It was found that this method is convenient [62] and preferable than the random generation method [14, 47]. In this method, the initial values of the weights and biases are selected so that the active regions of the transfer functions are used.

3.2.4 Activation functions

For nonlinear input–output experimental data, the neurons within the layers are processed through a nonlinear activation function \(f\) to obtain the output \(a\). Thus, for inputs vector \(X^{T}\) and weights \(W\) and bias vector \(b^{T}\), the output is given as [44],

$$X^{T} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \\ {x_{3} } \\ \end{array} } \\ { \, \vdots } \\ {x_{n} } \\ \end{array} } \right], \,\,\,W = \left[ {\begin{array}{*{20}c} {W_{11} W_{21} W_{31} \ldots W_{r1} } \\ {\begin{array}{*{20}c} {W_{21} W_{22} W_{32} \ldots W_{r2} } \\ \vdots \\ {W_{r1} W_{r2} W_{r3} \ldots W_{rn} } \\ \end{array} } \\ \end{array} } \right],\,\,\,\,\,b^{T} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {b_{1} } \\ {b_{2} } \\ \end{array} } \\ {b_{3} } \\ \end{array} } \\ { \, \vdots } \\ {b_{r} } \\ \end{array} } \right] \to a = f\left( {X^{T} W + b^{T} } \right)$$
(1)

where \(n\) and \(r\) are the numbers of the inputs and neutrons, respectively and \(f\) is an appropriate transfer function. It has been reported that the multilayer networks typically use sigmoid transfer functions in the hidden layers [12]. The \((logsig)\) and \((tansig)\) sigmoid transfer functions are defined by Eqs. (2) and (3), respectively.

$$f\left( x \right) = \frac{1}{{1 + e^{ - x} }}$$
(2)
$$f\left( x \right) = \frac{{e^{x} - e^{ - x} }}{{e^{x} + e^{ - x} }}$$
(3)

In fact, the tan-sigmoid function is a shifted and scaled version from the log-sigmoid function. The two functions are represented in Fig. 6.

Fig. 6
figure 6

A representation for the log-sigmoid and tan-sigmoid transfer functions used for the hidden layers

Full size image

The sigmoid functions transfer the input variable \(x\) to a scaled-range variable \(y\). The output variables of the log-sigmoid and tan-sigmoid transfer functions are scaled to [0, 1] and [− 1, 1], respectively. Furthermore, these two sigmoid transfer function are differentiable and thereby they fulfill the requirements of the backpropagation neural network [58]. However, there is no trustworthy evidence that supports applying these functions to any non-linear problem type [15]. Therefore, several trials have been carried out using different transfer functions. However, the optimum performance has been addressed using a log-sigmoid transfer functions for the first and second hidden layer, and tan-sigmoid transfer function with the third hidden layer. Of course, a linear transfer function was used for the output layer so that the output of the neural network will not be restricted to a finite range.

3.2.5 Training function and learning process

The backpropagation algorithm propagates the error back to the network in order to adjust the values of the weight and biases so that the error is minimized. Occasionally, the weights and bias are adjusted using the gradient-descent technique [16]. In this technique, the weight adjustment is proportional to the negative gradient of the error with respect to the weight according to [10],

$${W}_{k+1}={W}_{k}-\eta {\fancyscript{g}}_{k}$$
(4)

where \({W}_{k}\) is the weights and biases vector at epoch \(k\), \({\fancyscript{g}}_{k}=\partial {E}_{k}/\partial {W}_{k}\) is the gradient of the error function \(E\) with respect to the weight \({W}_{k}\) function, and \(\eta\) is the learning rate. Hence, the ANN approaches its optimum performance as the first derivative of the error function with respect to the weight approaches the zero, i.e. \(|\fancyscript{g}|\to 0\). However, updating the weights and biases based on this algorithm may lead to a local minimum. Therefore, Newton's methods [5, 6] were developed based on the second-derivative Hessian matrix of the error function with respect to weights/biases as

$${W}_{k+1}={W}_{k}-{A}_{k}^{-1}{\fancyscript{g}}_{k}$$
(5)

where \({A}_{k}\) is the Hessian second derivatives of the error with respect to the weight \({W}_{k}\). However, deducing the second-derivative of the error with respect to the weight would causes extensive computational time. Therefore, Levenberg–Marquardt suggested an approximated version of this method in which the Hessian matrix can be represented as [11, 36, 40]:

$$\mathcal{H}={J}^{T}J$$
(6)

where \(J\) is the Jacobian matrix consisting of the first derivative of the error function with respect to the weight. In this case, the gradient can be computed as:

$$\fancyscript{g}={J}^{T}e$$
(7)

Thus, the weights and biases are being updated using [11]:

$${W}_{k+1}={W}_{k}-{\left[{J}^{T}J+\mu I\right]}^{-1}{J}^{T}e$$
(8)

where \(\mu\) is the damping factor and \(I\) is the identity matrix. When \(\mu\) is zero, Eq. (8) turns into Newton’s method using approximated Hessian. At large \(\mu\) values, the Newton’s method turns into the ordinary gradient-descent method with small step size. Because Newton’s method is more efficient, \(\mu\) starts with relatively large initial value, and decrease for each successful step in which the error \(e\) decreases.

In the ANNs with multiple non-linear hidden layers, the overfitting and lack of generalization are very common problems [24]. This includes stopping the training as soon as performance on validation set starts to get worse. In this case, the network will memorize the training data, but still cannot interpret the new data. The best way to overcome this problem is to regularize a fixed-sized model that considers the average of the predictions resulted from the various settings of the network parameters [52]. Henceforth, the necessity of a regularization method which adapts the selected parameters and ensures the generalization of the ANN is inevitable [29]. Typically, the regularization function \({F}_{reg}\) should be considered in evaluation of the network performance instead of the usual mean square error \(mse\) function. Introducing the regularization \(\gamma\), the regularization function is defined as [11],

$$F_{reg} = \gamma \left( {mse} \right) + \left( {1 - \gamma } \right)\left( {msw} \right),\quad msw = \frac{1}{r}\mathop \sum \limits_{i = 1}^{r} w_{i}^{2}$$
(9)

It is clear that the determination of the regularization parameter \(\gamma\) value is the obstacle to using this method. Large \(\gamma\) values would cause in over fitting, and low values would cause in poor fitting. Bayesian regularization [35] was developed to automatically determine the optimal regularization parameters. In this technique, the weights and biases are considered random variable with certain distributions and are being updated using the Levenberg–Marquardt. The efficiency of this technique has been proven in difficult optimization problems [46], and therefore, it was implemented in the ANN toolbox MATALAB [21]. On the other hand, the Bayesian regularization function takes a long time compared with the usual Levenberg–Marquardt algorithm before it convergences [46]. Consequently, several parameters have been set in the current study to ensure that the network approaches the global minimum as follows:

  1. 1.

    The maximum epoch number has been set to 103 and the maximum training time has been expanded to infinity. This ensures the network will not stop because of insufficient epoch number or training time.

  2. 2.

    The target of the performance function \({F}_{reg}\) has been set to 0 to approach the best possible solution.

  3. 3.

    The minimum gradient limit has been set to \({10}^{-7}\) to approach the lowest change in the error function with respect to the weights and biases.

  4. 4.

    The damping factor \(\mu\) has been initially set to 0.005 and the maximum limit is \({10}^{10}\) with decreasing and increasing rates of 0.1 and 1.0, respectively. This is to ensure a wide range for the damping factor.

A comparison between the performance of the network using the usual Levenberg–Marquardt and using the Bayesian-regularization is illustrated in Fig. 7.

Fig. 7
figure 7

Performance of the ANN model designed using the Levenberg–Marquardt and Bayesian-Regulation training functions

Full size image

It is obvious that the lower levels of the gradient \(\partial E/\partial W\) and the mean square error \(mse\) could be reached using the Bayesian-Regulation training function than the case of using the usual Levenberg–Marquardt training function. It is worthwhile mentioning that the performance of the network has been also examined using other different training functions. However, the Bayesian-Regulation function still provides the optimum performance.

A way to ensure the generalization of the ANN is to monitor the performance of the network in both the training and testing stages. It is anticipated that the behavior of the ANN performance would be approximately identical in the two stages [38]. Therefore, in order to examine the generalization of the network, the data have been divided into two data sets. The first data set (70%) has been utilized in training the network, while the second data set (30%) has been used in testing the network. The results are reviewed in Sect. 4.1.

The incremental and batch modes are two algorithms used to update the values of the weights and biases in each layer. The incremental mode updates the weights and biases simultaneously after applying each input to the network. While the batch mode updates the weights and biases after applying all the input to the network [50]. In general, the incremental mode superiors the batch mode [32, 51] and it is recommended when the training data set is large [13]. However, this is not the case in the current study. Furthermore, two modes become identical at sufficiently small learning rate [18]. Hence, in the current study, batch mode was implemented as the initial learning method in the design of the neural network.

3.2.6 Software used

In the current study, the MATLAB (R2019a) has been used to build up the artificial neural network via the deep learning Toolbox. This toolbox provides a framework for designing and implementing deep learning networks with algorithms and retrained models. The processing functions and parameters required to design the ANN model are divided mainly into four input categories. The first and second input categories describes the dimensions of the ANN model including the size of the input and the output, the number layers, and the number of the neurons in each layer. They also specify the mathematical operations to be applied on the input and the output before the network starts the learning process. The third and fourth input categories concern the learning and the optimization processes. In these categories, all the connections between neural network components should be described via the synaptic weights and bias options. Moreover, the functions and the parameters of the learning and optimization processes should be determined.

4 Results and discussion

4.1 The performance of the artificial neural network

In the current study, the global optimization of the ANN model design has been validated throughout three evidences;

  1. 1.

    The performance of the network using the training data is similar to the performance of the network using the testing data (Fig. 8).

  2. 2.

    The linear correlation coefficients between ANN output and target are \(R>0.99\) for both the training and testing stages (Fig. 9).

  3. 3.

    The error of the ANN model design has a normal distribution (Fig. 10).

The performances of the network in case of using the training data and testing data have been monitored over the epochs (Fig. 8). The most important conclusion in Fig. 8 is that there is no significant difference between the performance of the ANN model in case of the testing process and in case of the training process. This indicates the generality of the ANN learning process and the designed model can be used for predicting new data.

Fig. 8
figure 8

Performance of the artificial neural network descripted in Table 1 for the train and test data set

Full size image

The ANN output and the target values have been also subjected to linear regression analysis (Fig. 9) and the correlation coefficient has been evaluated for the training data, test data, and all the data. It has been found that all the correlation coefficient values were \(R>0.99\) indicating a good linearity between the ANN output and the target values. This also implies that the performance of the ANN model design for the new data is similar to the performance of model for the training data.

Fig. 9
figure 9

Linear regression analysis for ANN output and the target values in cases of training, testing and all data. The correlation coefficients have been denoted in each case

Full size image

Usually, the error in the experimental measurements follows the Gaussian distribution with mean value zero. The error in the ANN output can be calculated as the difference between the target and the ANN output. The distribution of the ANN output error is presented in Fig. 10. It appears that the error of the ANN output has a Gaussian distribution with mean value around zero. This conclusion can be reported for both the training and testing processes. This also supports the evidence that the performance of the ANN model design has approached a global minimum. It also ensures the generality of the learning process of the ANN model design.

Fig. 10
figure 10

Distribution of the ANN output error k for the training- and test-data sets

Full size image

4.2 The standard uncertainty of the designed ANN model

One of the features of the ANN algorithm is that the solution is never exact. Indeed, each time the weights and biases are initiated, the ANN model would have a different solution. However, it would be useful to estimate the standard uncertainty of the ANN output for certainty replicated number. This standard uncertainty provides the range in which the ANN output should possible lie. However, in order to have a reliable standard uncertainty, the replicate number should not be < 30 [28]. Hence, the standard uncertainty of the ANN model design has been evaluated for 30 replicated number. The standard uncertainty has been estimated as [28]:

$$u\left(x\right)=\frac{s\left(x\right)}{\sqrt{n}}$$
(10)

where \(s\left(x\right)\) is the sample standard deviation, and \(n\) is the replicated number. This process is the same as conducting experimental measurements under the repeatability conditions. Figure 11 presents the percentage standard uncertainty of the evaluated dose rate predicted using the designed ANN mode at different dose-rate levels.

Fig. 11
figure 11

Uncertainty of the ANN output as a function in the dose-rate level

Full size image

It is obvious that the dose rate can be calculated with uncertainty < 2% in the dose-rate level \([10{-}100] \,{\text{mGy/h}}\) and with uncertainty less than 0.5% in the dose-rate level \([10^{2} {-}10^{3} ]{ }\,{\text{mGy/h}}\). For simplicity, an uncertainty of 2% can be used then for any value estimated from the ANN model design. However, it is always recommended to specify the uncertainty for each level or point for the measurand [28].

4.3 The bias in the designed ANN model

The bias in the ANN model designed has been estimated over different dose-rate points. These new points have not been used either in the training or validating processes. Furthermore, they have been chosen to cover the range of the experimental data. The dose-rate at these additional test points have been also measured by the ionization chamber system. A comparison between the accuracy of the results obtained by the neural network and the other interpolant algorithms is illustrated in Fig. 12.

Fig. 12
figure 12

Comparison between the accuracy of the output of the artificial neural network and the other interpolation algorithms

Full size image

A draw-back in the accuracy of the interpolation fitting methods can be clearly observed at the extreme low and high dose-rate. At low dose-rate, the error in the output computed by the interpolation fitting algorithms approached the 100% and even 500% levels. At the high dose-rate, the error in the output computed by the interpolation methods approached the 20% and in some cases approached the 50% levels. This is due to the fact that these methods estimate the dose-rate using the lines connecting neighboring evaluated dose points which is difficult to be determined at the extreme dose-rate values. Thereby, the interpolation fitting techniques can be used essentially to estimate values within the range of the fitted data [27]. Furthermore, the accuracy of these interpolation fitting methods varies over the different dose-rate level. Hence, selecting the appropriate interpolation fitting method would be a challenging task.

On the other hand, the artificial neural network model has shown a superiority over the interpolation fitting methods. This could recover the draw-back in the accuracy of the interpolation fitting method and succeeded to estimate the dose-rate at the extreme low- and high dose-rate levels with error not exceeding the 7% and 2% levels, respectively. At the intermediate dose-rate levels, the accuracy of the estimated dose-rate values was likewise better than the accuracy of the interpolation fitting method.

Once the accuracy of the neural network has been validated, it can be used for different dosimetric applications. A contour plot for the distribution of the dose-rate simulated using the artificial neural network model is shown in Fig. 13.

Fig. 13
figure 13

A contour plot for the dose-rate computed by the artificial neural network model. The dose-rate at each point has been represented by the average of 100 runs. In each run, the ANN parameteres have been reinitialized

Full size image

It worthwhile to mention that each dose-rate point in the contour plot has been evaluated under the repeatability conditions discussed in Sect. 4.2. The symmetry of the contour plot is observed at all the dose-rate levels. In other words, there was no unexpected behavior for the ANN model over the different dose-rate level. This, in fact, supports the reliability of using the designed model to estimate the dose-rate value at any point in the geometrical filed.

The ANN technique can be used to simulate and evaluate the dose distribution in human phantom which is widely used in diagnostic and therapeutic medical applications. Usually, the Monte Carlo algorithm is used for this purpose. However, it has been discussed previously the complexity of this algorithm. Therefore, the ANN modelling technique is expected have a great benefit in diagnostic and therapeutic applications.

5 Conclusions

  • The ANN modeling algorithm could successfully simulate the response of an ionization-chamber system to irradiator source.

  • The optimum performance of the ANN model could be approached with three hidden layers and a total number of 80 neurons.

  • The dose-rate could be evaluated by the designed ANN model with standard uncertainty < 2% for dose-rates less than \({10}^{2}\,{\rm mGy/h}\) and < 0.5% for dose-rates greater than \({10}^{2}\,{\rm mGy/h}\).

  • The errors in the evaluated dose-rate using interpolation methods have exceeded the 100% error level and approached the 20% error level for the dose rates less and greater than \(10\,{\rm mGy/h}\), respectively. While, the error in the evaluated dose-rate using the designed model did not exceed 7% and 2% for the same dose-rate levels, respectively.