1 Introduction

The management of radioactive waste is one of the main problems for the to-day mankind: during these last decades expensive and hard-realization proposals for achieving minor actinides burning or radionuclide transmutations have been proposed by International agencies [1]. At the moment, the deactivation mainly consists in mechanical processes, mainly the inertization where the waste is incorporated into a large volume of material, or using living organisms, e.g., Ralstonia detusculanense, an archaebacterium [2] able to significantly reduce the radioactivity of radionuclides coming from fission reaction (e.g., Co-60, Sr-90, Cs-135, Cs-137). Further, this crucial problem, i.e., reducing the radioactivity of nuclear (sanitary and industrial) wastes, has also mainly been addressed through the use of two main methodologies: mechanical and chemical-electrochemical methods. However, these methods do not modify the radioactivity of the single radionuclide but limit themselves to separate the radioactive fraction from all the rest of the material and, possibly, to concentrate it. In this way, the deactivation of a radioactive substance consists in incorporating it in a large volume of inert material: the result is a radioactivity decrease per unit of volume but the total number of radioactive nuclei is unchanged [3, 4].

Sugihara [5] proposed a treatment based on water at high pressure for deactivating fission products in radioactive soil/waste. All these procedures appear remarkable even if the theoretical bases are either not clear or not defined at all. The theories involved for justifying the radionuclide deactivation are different: the biquaternion quantum mechanics proposed by Conte [6], the Giuliano Preparata’s hypothesis [7], the Infoton theory by Brillouin [8] and Dirac [9], the Widom and Larsen [10] implemented by Srivastava et al. [11], the electronic density increase hypothesis [12], the nuclear lattice model by Dallacasa and Cook [13]. The common background for all these theories is the standard model of particle physics, under strict conditions and absolute observation both of the Minkowski space–time and of local Lorentz invariance. The problem is that they do not manage to explain some fundamental evidences, i.e., constant lack of radioactivity (γ radiation) and radioisotopes, formation of stable natural isotopes, modification of natural isotope ratio and anisotropic and asymmetric neutron emission [14,15,16,17,18].

The approach proposed in this paper follows the Deformed Space–Time (DST) theory, in not Minkowski conditions, in local Lorentz invariance breakdown [19, 20]; it is based on measurements of neutron and alpha emissions during different experiments without radioactivity production (i.e., gamma rays) [21,22,23].

2 Materials and methods

25 mL of 63Ni(NO)3 solution in nitric acid, after addition of 5 mL of ultrapure deionized water (resistivity 18 MΩ × cm−1) (total solution volume 30 mL, weight 39.6 g, density 1.32 g × cm−3), were subjected to cavitation process employing an Ergal 7075 sonotrode. This sample (i.e., 63Ni(NO)3) is quite similar to a real sample, the nuclide is a part of a molecule also containing other elements. This occurrence allows to extrapolate experimental conclusions to be extended to other applications. For instance, the sample is very corrosive, well simulating the case of nuclear wastes, either of industrial or sanitary source, that are the most critical to be treated. Thus, the reported experiment can be considered as a good test for future applications in severe conditions: radioactive and corrosive samples. The Ergal sonotrode is made of Al/Zn/Mg/Cu alloy with the following composition: Al 87.3–90%, Zn 5.1–6.1%, Mg 2.1–2.9%, Cu 1.2–2%, other elements are Fe, Mn, Si, Cr, Ti, Zr, 1.6–1.7%; its sizes are: height 85 mm, base diameter 30 mm, tip diameter 5 mm, according to the local Lorentz invariance breakdown rules for the DST reactions. The particular sonotrode shape and the angle between the vessel and the sonotrode are important experimental information and derive from our previous studies. Actually, the shape is well-described above whereas the angle cannot be reported because such data is the main frame of a patent pending. The sonotrode was immersed in the solution with the tip 4.5 mm far from the bottom of the vessel: an ultrasound generator produced ultrasounds at 35 kHz, 15 W transferred power and with a vibration amplitude of 7 µm. Two cavitation runs of 100 s, separated by a cooling interval of 5 min, were performed. Bremsstrahlung measurements were carried out by means of an X-gamma ATOMTEX AT6102 spectrometer equipped with a NaI detector, on the samples before/after cavitation using the same counting geometry (sample-detector distance 0.5 cm). A non-cavitated sample of equal volume (30 mL), weight (39.6 g) and density, was prepared in a similar vessel and measured in the same operating conditions, was used as blank solution. Furthermore, as a double check inductively coupled plasma-mass spectrometry (ICP-MS) measurements (Agilent mod. 7000) were carried out on all the samples (cavitated samples) and the references (non-cavitated samples).

3 Results and discussion

Before approaching the results, the choice of 63Ni should be addressed. The 63Ni is a beta negative emitter with a half-life of about one hundred years (101.2 ± 1.5 years): the bremsstrahlung of the beta radiation leads to an X-ray with a maximum of energy at 66 keV (end point).

Figure 1 reports the spectra of the background and of the sample before and after cavitation procedure.

Fig. 1
figure 1

Spectra obtained by NaI spectrometer before sonication and after 2 runs of 100-s (1st-run solid line, 2nd-run dot line) of sonication (35 kHz, 15 W). The background radiation spectrum is reported (grey line)

Full size image

As it can be seen, the useful field energy ranging between 0 and 66 keV does not show any interferences in the background whereas a clear decrease before and after cavitation (from 2380 counts to 2046 counts after two cavitation runs, with a coefficient of variation, cv%, of 4.6% and 5.4%, respectively) of the 63Ni radioactivity can be evidenced, with a maximum peak around 30 keV (i.e., the average energy of the γ emitted) (Fig. 2). Different tests were carried out for attesting this decrease and obtaining a statistical trial: varying the cavitation time and the time interval between the two different cavitation procedures such decrease ranges between 13 ± 6% and 14 ± 6%.

Fig. 2
figure 2

Spectra of bremsstrahlung radiation of beta electrons emitted by 63Ni obtained before sonication and after two-runs of 100-s sonication (35 kHz, 15 W). The background has been subtracted

Full size image

A confirmation of this occurrence has been proved analyzing the same samples by means of ICP-MS: the mass spectrometry tests performed on blank and samples before and after cavitation have confirmed a decrease around 14%. Simultaneously, an interesting detection of an increasing of non-radioactive nuclides (e.g., 59Co, 7Li, 9Be, 11B) has been detected (Table 1).

Table 1 Differences (Δ, expressed as %) between samples treated with ultrasound and untreated ones (Atomic number Z; Mass number A)
Full size table

This occurrence is important because, confirming what reported by Metzler et al. [24] about the absence of energetic nuclear radiation (the authors studied the decay of nucleus 57Co into 57Fe), it strengthens data obtained by our experiments. Further, it could appear as a confirmation of the DST theoretical hypothesis: during the ultra-sound cavitation treatment of material containing radioactive species (e.g., fission products, reactor wastes, radiogenic materials used in medical applications): a radionuclide transformation evidenced by a clear radioactivity decrease is obtained. The observed phenomenon cannot be considered a bioconcentration process, neither a radionuclide confinement nor a nuclear transmutation, neither a decay time acceleration. We called it “Normalization of the radionuclide”, meaning the occurrence of a nuclear transformation reaction under the Deformed Space–Time conditions: the transformation of a radioactive nucleus into a stable non-radioactive nucleus without radioactivity emission.

The strict observance of the experimental conditions/parameters following our experiences performed on the basis of the DST theory, is fundamental for the experiment success. Previous experiments performed by means of electromagnetic field variation and neutron emission measurements, showed that there are preferential and privileged spatial directions within which the phenomenon occurs and is able to maintain itself [23]. Outside of these conditions, the phenomenon does not occur, or occurs in a weak way, or is not maintained. In the experiment reported in this paper, the angles formed by sonotrode with the vessel and with the ultrasound transmitter were chosen to give the neededand privileged spatial directions. In this way, the reaching of an exact energy density and intensity according to the sources and material used (e.g., ultrasounds, electromagnetic waves, spark source ionization) is an important starting point as well as its constant maintenance, the threshold time for triggering the process, the temporal and spatial sonotrode symmetry in relationship to the correct energy administration and, finally, the presence of DST micro-reactors (bubbles) within the treated material [25]. The addition of 5 mL of fresh ultrapure deionized H2O (Resistivity 18 MΩ × cm−1) to 63Ni(NO)3 solution was deliberately performed for creating the correct conditions for the formation of micro reactors, i.e., bubbles with a diameter not exceeding 10 µm. These conditions allow to occur the DST reactions, as shown in our previous paper [26, 27] both for liquids/solutions, and for solid state materials.

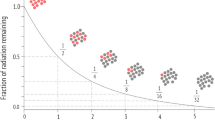
As reported above, this normalization “causes” an average radioactivity decrease of 14% among the experiments. For getting an idea about the results obtained, Fig. 3 shows the 63Ni natural decay both under normal working conditions and after cavitation process.

Fig. 3
figure 3

Trends of the 63Ni decay according to the exponential decay law (dot line) and after the cavitation procedure (solid line): in the 2nd case it can be noted the gain

Full size image

63Ni has a life-time of 101.2 ± 1.5 years: it means that, for obtaining the radioactivity decrease recorded by our experiments, more than 20 years would be needed (dotted line) whereas two moderate cavitations of 100 s were sufficient to achieve more remarkable results (solid line). The step-down between the two lines is really evident at the beginning, i.e., when the cavitation produces its effects on the material. From this point on, after the end of the cavitation effects that shortened the decay of 22 years, the radioactivity asymptotically decreases down to the dotted line according to the exponential decay law. It should be noted that the step-down is only due to the radioactive nuclei reduction, which means that the decay constant is not modified by the cavitation process.

Briefly resuming, three issues are noteworthy to be stressed. First, the result confirmation already achieved in thorium experiments [22] showing the same behavior as in nickel: the radiation reduction exactly matches the radionuclide reduction. Second, the time elapsed between the thorium and the nickel experiments has been fulfilled by the mercury metamorphosis experiments [25] which, together with the neutron asymmetry emission experiments, allows to understand the right coupling between sonotrode and vessel as well as their right shapes and dimensions. Third, here is shown another proof that in Deformed Space–Time reactions the use of a privileged angle is fundamental (together with the energy thresholds and energy densities) in order to start and sustain the reaction regardless the material (radioactive or stable) subjected to.

4 Conclusions

The considerations here reported pave the way to new methods to treat useless radioactive substances (e.g., wastes) from nuclear or medicine industry. The data obtained are precise and accurate but not definitive. The present experiment confirms the existence of the phenomenon, which must be verified by means of further tests. We stress that the normalization of a radioactive substance induced by DST reactions, is only due to its transformation in stable elements and neither to any alteration of the radioactive decay law nor to a leptonic interaction deviation. In future studies, the main objectives should be either both the use of other radionuclides (α, β and γ emitters) at well-defined specific activity, either the statistical quality improvement of the results either the control of the transformation products. The large idea is to extend the applications of the DST theory to the main elements involved in the radiological wastes, e.g., transuranic elements or fission products (137Cs). Finding these extension means to have a powerful tool for addressing studies of radioactivity removal. If nuclear wastes are well-known issues, the medical wastes, both radioactive and no-radioactive, will be one of the main target in the future according to the great daily disposals created by all the hospitals worldwide. All the reported uses are only the main applications but the scenarios that could open up are substantially so big to include, for instance, the treatment of industrial wastes and garbage.