Quadrotors in factory applications: design and implementation of the quadrotor’s P-PID cascade control system

Abstract

This paper describes the current legal framework and regulations applied to industrial drone’s flights established by different countries as a set point on drones design and applications. We present a mathematical approach used to build the structure of an attitude controller for a quadcopter (drone) as to answer the question of ’How to implement an attitude controller on a quadcopter for indoor and outdoor flights as a step forward to support the safety features in factory applications’. The control system was designed for a quadcopter on ’$\times$’ configuration, which allows it to have six degrees of freedom (6DOF) of movement, while commanded by four inputs given by the radio controller (R/C). Accelerometers and gyroscopes were used in order to obtain the data related to the drone’s behavior during the flight to be able to control it. A cascade controller P-PID was implemented in order to control the system and reach the stability as well as in indoor or outdoor flights. The theories presented in this paper were analyzed and proved on a real model resulting in the desired flying behavior.

1 Introduction

A quadrotor or quadcopter belongs to the family of unmanned aerial vehicles (UAV), and it consists of two pairs of counter-rotating rotors and propellers, located at the vertex of a square frame. It is capable to perform vertical take-off and landings (VTOL), similar to the typical helicopters. However, the control system between helicopters and quadcopters significantly differs from one to the other due to the flying dynamics, respectively [1].

According to the research made by Grand View Research on their market research report on 2016 [2], the use of drones in the industry has considerably increased in the last years and it will continue growing. Recently, we have seen an increase in the application of drones in the existing industries. By using drones, it is possible to perform operations that could be harmful to humans or that would require more invest of resources if done by humans, i.e., it would require fewer resources to use a drone to check up the condition of machinery, structures or infrastructures located on remote areas or considerably high altitude with respect to the ground, patrol certain areas, transportation, deliveries and even data collection [3]. Another use of the UAVs is image recognition and mobile 3D mapping, where the drone takes pictures or to scan certain areas as to be able to build a virtual model of the selected area [4]. These applications could bring benefits to the area of civil engineering and factory planning [5]. In those applications, a UAV will take images of the real environment and then those images would be analyzed and processed as to get a digital version of the real environment to work with.

According to Kampker [6], the use of drones could be implemented as part of the production technology in the e-mobility production under the concept of smart logistics. This concept, contrary to the classical sequential approach, requires flexibility based on the dynamic and continuous resequencing of the assembly objects. Therefore, the use of drones in industrial applications could be beneficial to develop. New concepts related to logistics, for example, the concept of 3D logistic developed by Kampker [6], allow the usage of the third dimension for internal logistics processes.

This paper covers the path from the statement of the problem ’How to implement an attitude controller on a quadcopter for indoor and outdoor flights as a step forward to support the safety features in factory applications’, to the modeling, simulation and implementation of the control system on a real-life-based application. The approach presented in this paper is based on a customized quadcopter developed by the Institute of Automatic Control Engineering (RST) at the University of Siegen, Germany [7]. Founded on the work developed by Brehm [7], this customized quadcopter was built using the DJI Quadcopter kit F450. By using this frame as the base of our quadrotor, as shown in Fig. 1, the motors physical distribution was fixed to work on an’$\times$’ configuration.

Fig. 1

Quadcopter DJI flame wheel F450 [8]

In order to establish the control system, it is needed to collect certain data linked to the flying behavior of the quadcopter, i.e., the position, height and accelerations of the flying platform by using specialized sensors for this task. The inertial measurement unit (IMU) used was the UM7-LT Orientation Sensor developed by CHRobotics [9]. This IMU has gyroscopes and accelerometers that could send the data directly either on Euler angles or quaternions.¹ For this project, the Euler angles output was chosen over the quaternions, due to the convenience of the data based on our approach considered building the mathematical model of the system. The data coming from the sensors are received by the microcontroller² ($\mu C$), then it is processed in order to control the behavior of the quadcopter and the output signal is sent directly to the motor drivers.

The proposed control system was designed to allow either indoor or outdoor flights, considering the safety of the users as an important parameter of design. To satisfy this criterion, the system should be robust, fast and reliable at the same time. The novelty of this paper is due to the introduction of a control system based on cascade control theories applied on a fully customized quadcopter. Two controllers, one in charge of the angular position and the other for rate movement, were set in a cascade configuration to guarantee the stability and reliability of the system.

2 Flying regulations: legal framework

To implement the use of drones as part of the daily activities in the industry, it is needed to follow the regulations specified by the country of residence. The organization that gives the rules to follow while flying drones in the countries inside the European zone, Switzerland, Norway, Iceland and Liechtenstein is the European Aviation Safety Agency (EASA) . In Germany, the regulations regarding this matter can be found in the Air Traffic Licensing Regulation and the Air Traffic Regulation of the country. Quadcopters as a flying platform have to follow this regulation because those will develop most of their activities in the air. (This statement applies for both outdoor and indoor flights.)

At the beginning of 2017, new drone regulations were introduced on the aerospace laws in Germany. Significant changes were made in the Regulation to Regulate Unmanned Aerial Vehicles (Verordnung zur Regelung des Betriebs von unbemannten Fluggeräten) [12], Federal Law Gazette–Air Traffic Licensing Regulation on the section I 683 (Nr. 17) (BUNDESGESETZBLATT [BGBl.] - Luftverkehrs-Ordnung (LuftVO)) [13] and in the Air Traffic Licensing Regulation (Luftverkehrs Zulassungs Ordnung) [14]. In order to see what rules apply to our applications, we need a definition of what is it considered as a drone. According to German Air Traffic Act - Federal Law Gazette Art.1 [15], the term drone just applies to Unmanned Aerial Vehicles (UAV), including their control stations, which are not used for hobby or recreational purposes and the ones used for recreational purposes are defined as model aircraft. However, the laws stated before applying for both terms.

2.1 Prohibitions and restrictions

It is possible to find some similarities between the UAVs rules set in different countries, even though the regulatory agencies are independent between them (see Table 1). For example, common rules among different countries are that the drones should not fly 100–120 m above the ground; it is not allowed to fly over large groups of people, as well as to perform flights during the nighttime.

Table 1 Table of control agencies in charge of the flying regulations per country [16,17,18,19,20]

For industry projects, different kinds and customized drones could be used, especially for drones specialized in transportation activities. Some of them could have a weight equal to or greater than 2 kg, see Table 2.³ Therefore, specific rules apply to these flying platforms. This means that in order to fly those devices, the user will need certifications to demonstrate that they have specialized knowledge to operate those devices under the respective legal framework. This certification could be either a pilot license or a similar certificate from an agency recognized by the respective aviation authorities. Additionally, it might be needed to obtain certain authorizations to fly granted by the relevant state aviation authority to perform flights, specially if the dimensions/weight of the total platform exceed 5 kg, by flying them at nighttime (between the end of evening civil twilight and the beginning of morning civil twilight) or in certain defined areas [23].

Table 2 Table of common heavy lifting drones in the actual market

The application of UAVs in the industry based on the German regulations leads restrictions on the use and the design criteria [12] of these devices. Some of the most relevant prohibitions of the use of drones or model aircraft are listed below.

• 1. Aircrafts or drones weighing more than 25 kg.

• 2. Performing flights.

  Within 100 m of or above people and public gatherings, the scene of an accident, disaster zones, other sites of operation of police or other organizations with security-related duties, and military drill sites, correctional facilities, military complexes, industrial complexes, power plants, and power generation and distribution facilities, hospitals, property of federal or state governments, diplomatic or consular missions, international organizations, and law enforcement and security agencies, federal highways, federal waterways, and railway systems, nature reserves.

  Above residential property if the drone or model aircraft weighs more than 0.25 kg.

• 3. If it is able to receive, transmit, or record optical, acoustic, or radio signals in the zones described by the item 2.

• 4. In controlled airspace.

• 5. To transport explosives, pyrotechnic articles, radioactive materials, or hazardous materials.

Considering the points 1, 2, and 5, the implementation of quadcopters in industrial applications has significant restrictions on the maximum weight, flying zones and the objects able to transport.

On the matter of other countries where the agency EASA have jurisdiction (see Sect. 2), the flying space is restricted by the concept of the Urban-space (U-space). This term was adopted by the European Commission for a set of services supporting low-level drone operations (below 120 m) and it will ensure that drones do not enter any restricted zones.

3 Design criteria

It is needed to know exactly which regulations to follow and the technical requirements to start with the design of the quadcopter. Therefore, it is important to take in consideration where the flights are going to be held, as do not incur any violation of the laws and regulation. Additionally, it is important to establish the maximum weight of the flying platform based on the law limitations as design criteria.

Our design is based on the following ideal parameters⁴:

• Maximum weight without load:

    980 g (+/− 98 g) (4 s, 14,8 V)

    400 g (+/− 40 g) (3 s, 11,1 V)

• Flight time:

  Battery (4 s, 2200 mAh), ca. 8–10 min. Weight: 580 g

  Battery (4 s, 4000 mAh), ca. 18 min. Weight: 580 g

Once the desired parameters are set, the next step is to design the control system (see Sects. 8.1 and 9). However, it is needed to understand in detail the system to be controlled before to proceed to build the control system.

4 Flight mechanism

The whole quadcopter setup consists of two clockwise rotating motors and two counter-clockwise rotating motors on the vertex of a square framework, as it is seen in Fig. 2). The movement in space is achieved by the variation of the final force and torque on each axis. To achieve the right variation of the torque and force on the system, the motors are configured to work on pairs, as shown in Table 3.⁵ M1, M2, M3 and M4 are considered Motor-1, Motor-2, Motor-3 and Motor-4, respectively.

Fig. 2

Quadcopter setup

Table 3 Motors configuration

The quadcopter translational motion requires tilting the platform toward the desired axis. The reference angle of the quadcopter is given by the roll $\phi$, pitch $\theta$, yaw $\psi$ convention of movement in three dimensions (3D), see Fig. 3.

Fig. 3

Notation for movement in 3D

Based on the motors’ arrange described in Table. 3, it is just needed to change the speed of one of the pair of motors as to cause motion in six degrees of freedom (DOF). This is the reason that allows the quadcopter to move in six DOF and be controlled just with four inputs [24].

4.1 Movements

The flight dynamic of the quadrotor is based on the relationship between the angular speed of the motors, i.e., the lifting force ($F_{t}$) and final torque ($\tau _{t}$) produced by the motors and applied on the quadrotor. Four movements are achieved with the variation of $F_{t}$ and $\tau _{t}$:

• 1. Vertical ’z’ It is produced by the summation of all the rotor forces on the z-axis.

• 2. Pitching ’$\theta$’ This movement is achieved by manipulating the final torque around the y-axis. This is done by the change of the front rotors speed against the back rotors (increasing or decreasing the speed according to the desired movement).

• 3. Rolling ’$\phi$’ The principle behind this movement is the same as with the pitching, but the new reference axis is x. Left and right rotors provide the rolling movement.

• 4. Yawing ’$\psi$’ The yaw motion is generated by the rotors reactive torque. This motion is introduced by different rotational speeds applied to the pair of counter-rotating motors. It causes a difference of torque between them and exerts a final torque around the z-axis.

5 Mathematical modeling

Normally two approaches are used to develop the mathematical model of most of the mobile robots [25]:

• Newton–Euler equations.

• Lagrangian equations.

In this paper, we would like to focus our mathematical model on the classical approach given by Newton’s laws; therefore, we develop our model based on the Newton–Euler equations. Based on those theories, the quadcopter should be described as a rigid body that moves through different reference frames based on a fixed coordinate system. Those help us to describe the position of orientation of the flying platform in the space.

Fig. 4

Vehicle frame $F^{v}$

5.1 Coordinate system

First, it is necessary to understand how the quadcopter moves in the space (see Sect. 4.1) and which moves are associated with each reference frame. Those help us to understand how objects move in the space and how to mathematically represent them. Next presented are the frames that describe the quadcopter’s dynamic.

• Inertial frame $F^{i}$: earth-fixed coordinate system.

• Vehicle frame $F^{v}$: The origin is the center of mass of the quadcopter and it is aligned with $F^{i}$.

• Body Frame $F^{b}$: $F^{v}$ rotated on $\phi ^{+}$, see Eq. 4.

  The vectors on the vehicle frame $F^{v}$ are described by the matrix given in Eq. 1.

  $$\begin{aligned} F^{v}(1) = \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix} \end{aligned}$$

  (1)

  The vehicle frame vectors corresponding to the ’$F^{v}$’ matrix (see Fig. 4) are considered the base for our reference frames’ analysis. The initial part of this analysis consists on the rotation of the vector frame ’$F^{v}$’ with respect to some specific axis as to create our mathematical references to analyze the movements in the 3D space.

• Vehicle-1 frame $F^{v1}$: Based on $F^{v}$ but rotated in $\psi ^{+}$, Fig. 5a.

  $$\begin{aligned} R_{z}(\psi ) = \begin{pmatrix} \cos (\psi ) &{}\quad -\sin (\psi ) &{}\quad 0 \\ \sin (\psi ) &{}\quad \cos (\psi ) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix} \end{aligned}$$

  (2)

• Vehicle-2 frame $F^{v2}$: Based on $F^{v1}$ but rotated in $\theta ^{+}$, Fig. 5b.

  $$\begin{aligned} R_{y}(\theta ) = \begin{pmatrix} \cos (\theta ) &{}\quad 0 &{}\quad \sin (\theta ) \\ 0 &{}\quad 1 &{}\quad 0 \\ -\sin (\theta ) &{}\quad 0 &{}\quad \cos (\theta ) \end{pmatrix} \end{aligned}$$

  (3)

• The body frame $F^{b}$: Based on $F^{v2}$ but rotated in $\phi ^{+}$, Fig. 5c.

  $$\begin{aligned} R_{x}(\phi ) = \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \cos (\phi ) &{}\quad -\sin (\phi ) \\ 0 &{}\quad \sin (\phi ) &{}\quad \cos (\phi ) \end{pmatrix} \end{aligned}$$

  (4)

Fig. 5

Vehicle frames

Once the coordinate frames are defined, it is possible to represent movements from one frame to another by using two operations: rotations and translation [10]. In this case, the rotation matrix to go from the body frame $F^{b}$ to the vehicle frame $F^{v}$ is defined by

$$\begin{aligned} R^{v}_{b}(\psi ,\theta ,\phi )= \quad& {} R^{v}_{v1}(\psi )~R^{v1}_{v2}(\theta )~R^{v2}_{b}(\phi )\nonumber \\ R^{v}_{b}(\psi ,\theta ,\phi )= \quad &\begin{pmatrix} C\psi ~C\theta ;{} &\quad C\psi ~S\theta ~S\phi - S\psi ~C\theta ; &{}\quad C\psi ~S\theta ~C\phi + S\psi ~S\phi \\ S\psi ~C\theta ; &{}\quad S\psi ~S\theta ~S\phi + C\psi ~C\phi ; &{}\quad S\psi ~S\theta ~C\phi - C\psi ~S\phi \\ -S\theta ; &{}\quad C\theta ~S\phi ; &{} \quad C\theta ~C\phi \end{pmatrix} \end{aligned}$$

(5)

Defining: $Cx= \cos (x)~;~Sx=\sin (x)$.

6 Kinematics & dynamics analysis

6.1 Kinematics

The first step is to define the linear velocity in the vehicle frame as shown in Eq. 6

$$\begin{aligned} \dfrac{d}{dt} \begin{pmatrix} x^{i}\\ y^{i}\\ z^{i} \end{pmatrix} =~ R^{v}_{b} \begin{pmatrix} v_{x}^{~b}\\ v_{z}^{~b}\\ v_{z}^{~b} \end{pmatrix} = \begin{pmatrix} v_{x}^{~i}\\ v_{z}^{~i}\\ v_{z}^{~i} \end{pmatrix} \end{aligned}$$

(6)

Secondly, we define the angular velocity like $w_{b} = \begin{pmatrix} p&\quad q&\quad r \end{pmatrix}^{T}~$ and consider that the range of the angle derivation will be less or equal to ±/,20 grades; therefore, it is possible to use the criteria of small angle approximation.⁶

By combining the definition of the angular velocity described above and the concepts shown in Sect. 5.1, it is possible to obtain the angular velocity by following the steps given by Eqs. 7, 8).

$$\begin{aligned} \begin{pmatrix} p \\ q \\ r \end{pmatrix}= & {} R_{v2}^{b}(\dot{\phi }) ~ \begin{pmatrix} \dot{\phi } \\ 0 \\ 0 \end{pmatrix} + R_{v2}^{b}(\dot{\phi }) ~ R_{v1}^{v2}(\dot{\theta }) \begin{pmatrix} 0 \\ \dot{\theta } \\ 0 \end{pmatrix}\nonumber \\&+ R_{v2}^{b}(\dot{\phi }) ~ R_{v1}^{v2}(\dot{\theta }) ~ R_{vv}^{v1}(\dot{\psi }) \begin{pmatrix} 0 \\ 0 \\ \dot{\psi } \end{pmatrix} \end{aligned}$$

(7)

$$\begin{aligned} \begin{pmatrix} p \\ q \\ r \end{pmatrix}= & {} \begin{pmatrix} 1 &{}\quad 0 &{}\quad -\sin (\theta ) \\ 0 &{}\quad \cos (\phi ) &{}\quad \sin (\phi )~\cos (\theta ) \\ 0 &{}\quad -\sin (\phi ) &{}\quad \cos (\phi )~\cos (\theta ) \end{pmatrix} ~ \begin{pmatrix} \dot{\phi } \\ \dot{\theta } \\ \dot{\psi } \end{pmatrix} \end{aligned}$$

(8)

Now, isolating the angular velocities on the vehicle frame

$$\begin{aligned} \begin{pmatrix} \dot{\phi } \\ \dot{\theta } \\ \dot{\psi } \end{pmatrix} = \begin{pmatrix} 1; &{}\quad \sin (\phi )~\tan (\theta ); &{}\quad \cos (\phi )~\tan (\theta ) \\ 0; &{}\quad \cos (\phi ); &{}\quad -\sin (\phi ) \\ 0; &{}\quad \sin (\phi )~\sec (\theta ); &{}\quad \cos (\phi )~\sec (\theta ) \end{pmatrix} \begin{pmatrix} p\\ q \\ r \end{pmatrix} \end{aligned}$$

(9)

6.2 Rigid body dynamics

Newton’s second law⁷ is defined by Eq. 10 for translational motion.

$$\begin{aligned} m~\frac{d^{2}x}{dt^{2}} = m\frac{dv}{dt_{i}} = m~a = F \end{aligned}$$

(10)

Applying the Coriolis effect to Eq. 10, we obtain

$$\begin{aligned} m\frac{dv}{dt_{i}} = m\left(\frac{dv}{dt_{b}} + w_{b/i}~\times ~v \right) = F \end{aligned}$$

(11)

where $w_{b/i}$ is the angular velocity of the airframe with respect to the inertial frame.

In order to obtain the linear acceleration in the body frame, it is necessary to isolate $\frac{dv}{dt_{b}}$.

$$\begin{aligned} \begin{pmatrix} \dot{v}_{x}^{~b} \\ \dot{v}_{y}^{~b} \\ \dot{v}_{z}^{~b} \\ \end{pmatrix}= & {} \frac{1}{m} \left\{ -m \begin{pmatrix} \hat{i} &{}\quad \hat{j} &{}\quad \hat{k} \\ p &{}\quad q &{}\quad r \\ v_{x}^{b} &{}\quad v_{y}^{b} &{}\quad v_{z}^{b} \end{pmatrix} + \begin{pmatrix} F_{x} \\ F_{y} \\ F_{z} \end{pmatrix} \right\} \end{aligned}$$

(12)

$$\begin{aligned} \begin{pmatrix} \dot{v}_{x}^{~b} \\ \dot{v}_{y}^{~b} \\ \dot{v}_{z}^{~b} \\ \end{pmatrix}= & {} \begin{pmatrix} v_{y}^{~b}~r - v_{z}^{~b}~q \\ v_{z}^{~b}~p - v_{x}^{~b}~r \\ v_{x}^{~b}~q - v_{y}^{~b}~p \end{pmatrix} + \frac{1}{m} \begin{pmatrix} F_{x} \\ F_{y} \\ F_{z} \end{pmatrix} \end{aligned}$$

(13)

For the calculus of the angular acceleration on the body frame, it is necessary to apply the 2${\mathrm{nd}}$ Newton’s law for the rotation motion and include the Coriolis effect.

$$\begin{aligned} \frac{dH^{b}}{dt_{i}} = \frac{dH^{b}}{dt_{b}} + w_{b/i} \times H^{b} = \sum \tau ^{b} \end{aligned}$$

(14)

The angular acceleration in the body frame is obtained by expressing Eq. 14 in body coordinates and isolating $\frac{dw^{b}}{dt_{n}}$.

$$\begin{aligned} \begin{pmatrix} \dot{p} \\ \dot{q} \\ \dot{r} \end{pmatrix} = \begin{pmatrix} \frac{J_{y}-J_{z}}{J_{x}}~qr \\ \frac{J_{z}-J_{x}}{J_{y}}~pr \\ \frac{J_{x}-J_{y}}{J_{z}}~pq \\ \end{pmatrix} + \begin{pmatrix} \frac{1}{J_{x}}\tau _{\phi } \\ \frac{1}{J_{y}}\tau _{\theta } \\ \frac{1}{J_{z}}\tau _{\psi } \\ \end{pmatrix} \end{aligned}$$

(15)

Fig. 6

Quadcopter ideal model

For the calculus of the inertias, it is assumed an ideal model as observed in Fig. 6. The quadcopter is assumed with a spherical dense center with mass M and radius R. The motors are modeled like four point of masses located at a distance l from the center with mass m. With those parameters clear, it is now possible to calculate the corresponding inertia of the whole system (Fig. 6).

$$\begin{aligned} J_{x}= & {} J_{y} = \frac{2MR^{2}}{5} + 2ml^{2} \end{aligned}$$

(16)

$$\begin{aligned} J_{z}= & {} \frac{2MR^{2}}{5} + 4ml^{2} \end{aligned}$$

(17)

6.3 Forces and moments

The forces and moments on the quadcopter described on the Fig. 7 are primarily due to the gravity and the four propellers.

Fig. 7

Forces and moment on the quadcopter (ideal)

Each motor produces an upward force F and a torque $\tau$. Thus, the total force of the quadcopter is given by the sum of all the forces ($F_{t}=\sum _{i=1}^{4}F_{i}$). The same principle applies for the torque ($\tau _{t}=\sum _{i=1}^{4}\tau _{i}$).Considering this, the rolling, pitching and yawing torques are defined.

$$\begin{aligned} \begin{pmatrix} \tau _{\phi } \\ \tau _{\theta } \\ \tau _{\psi } \end{pmatrix} = \begin{pmatrix} l(F_{d}-F_{b}) \\ l(F_{a}-F_{c}) \\ (\tau _{b}+\tau _{d})-(\tau _{a}+\tau _{c}) \end{pmatrix} \end{aligned}$$

(18)

The force of gravity is also exerting a force on the vehicle frame $F^{v}$ of the quadcopter, and it just has an influence on the z direction. However, in order to match this force with the reference given on the body frame $F^{b}$, it is necessary to multiply by the respective rotation matrix.

$$\begin{aligned} F_{g}^{v} = R_{v}^{b}~F_{g}^{b} \longrightarrow F_{g}^{v} = \begin{pmatrix} -mg~\sin (\theta ) \\ mg~\cos (\theta )~\sin (\phi ) \\ mg~\cos (\theta )~\cos (\phi ) \end{pmatrix} \end{aligned}$$

(19)

Finally, rewriting Eq. 13, we express the linear acceleration on the body frame as Eq. 20.

$$\begin{aligned} \begin{pmatrix} \dot{v}_{x}^{~b} \\ \dot{v}_{y}^{~b} \\ \dot{v}_{z}^{~b} \\ \end{pmatrix} = \begin{pmatrix} v_{y}^{~b}~r - v_{z}^{~b}~q \\ v_{z}^{~b}~p - v_{x}^{~b}~r \\ v_{x}^{~b}~q - v_{y}^{~b}~p \end{pmatrix} + \begin{pmatrix} -g\sin \theta \\ g\cos \theta ~\sin \phi \\ g\cos \theta ~\cos \phi \end{pmatrix} + \frac{1}{m} \begin{pmatrix} 0 \\ 0 \\ \sum F \end{pmatrix} \end{aligned}$$

(20)

7 Simplified model

The idea behind the mathematical model is to make possible the development of a control system. However, if the model is too complex, the design of the control system will be complicated too. For the previous model is possible to assume some simplifications without losing significant precision of the motion behavior.

Assuming that $\phi$ and $\theta$ are small angles, the angular velocity will be described as Eq. 21.

$$\begin{aligned} \begin{pmatrix} \dot{\phi } \\ \dot{\theta } \\ \dot{\psi } \end{pmatrix} = \begin{pmatrix} p \\ q \\ r \end{pmatrix} ~;~ F^{i} \end{aligned}$$

(21)

Also, it is possible to assume that the Coriolis terms qr, pr and pq are small and negligible. Simplifying Eq. 15, the simplified version of the angular acceleration is obtained in Eq. 22 .

$$\begin{aligned} \begin{pmatrix} \dot{p} \\ \dot{q} \\ \dot{r} \end{pmatrix} = \begin{pmatrix} \frac{1}{J_{x}}~\tau _{\phi } \\ \frac{1}{J_{y}}~\tau _{\theta } \\ \frac{1}{J_{z}}~\tau _{\psi } \\ \end{pmatrix} \end{aligned}$$

(22)

Combining Eqs. 21 and 22, the angular acceleration on the Vehicle Frame⁸ is obtained and represented by Eq. 23.

$$\begin{aligned} \begin{pmatrix} \ddot{\phi } \\ \ddot{\theta } \\ \ddot{\psi } \end{pmatrix} = \begin{pmatrix} \frac{1}{J_{x}}~\tau _{\phi } \\ \frac{1}{J_{y}}~\tau _{\theta } \\ \frac{1}{J_{z}}~\tau _{\psi } \\ \end{pmatrix} ~;~ F^{v} \end{aligned}$$

(23)

For the linear acceleration, we will consider that the Coriolis effect terms do not have an important influence. Also, we will reflect each force on the vehicle frame $F^{v}$.

$$\begin{aligned} \begin{pmatrix} \dot{v}_{x}^{v} \\ \dot{v}_{y}^{v} \\ \dot{v}_{z}^{v} \end{pmatrix}= & {} R_{b}^{v}~ \begin{pmatrix} v_{x}^{b} \\ v_{y}^{b} \\ v_{z}^{b} \end{pmatrix} \end{aligned}$$

(24)

$$\begin{aligned} \begin{pmatrix} \dot{v}_{x}^{v} \\ \dot{v}_{y}^{v} \\ \dot{v}_{z}^{v} \end{pmatrix}= & {} \begin{pmatrix} 0 \\ 0 \\ g \end{pmatrix} + \frac{F}{M}~ \begin{pmatrix} -\cos (\psi )~\sin (\theta )~\cos (\phi ) + \sin (\psi )~\sin (\phi ) \\ -\sin (\psi )~\sin (\theta )~\cos (\phi ) - \cos (\psi )~\sin (\phi ) \\ -\cos (\theta )~\cos (\phi ) \end{pmatrix} ;~ F^{v} \end{aligned}$$

(25)

Where the force F is a vector with influence on each of the related components

7.1 Motors modeling

The motor’s and propellers’ models selected for the quadcopter were the DJI-2212 920 KV and the DJI 9443 self-locking props (plastic blades, see Fig. 8), respectively. The power of the system is provided by two lithium-ion-polymer batteries⁹ 4 s (14.8 V), one with 2200 mAh and the other with 4400 mAh (see Fig. 9).

Fig. 8

Propellers DJI 9443 self-locking (plastic)

Fig. 9

Batteries 4 s. 2200–4000 mAh

Considering the study made by Jackerbes [26] on that model of motors, it was possible to determine the behavior of the motors on their different states of work, as shown in Fig. 10. By knowing the data from the motors and the equivalence from the input capture function on the microcontroller, as well as the PWM signal [7], a table that describes motors behavior was built.

Fig. 10

Eagle tree eLogger V4- acquired data [26]

The values provided in Table 4 were obtained through the software and hardware given by Eagle Tree eLogger [26] and the microcontroller-type pic33ep512mu810 [7].

Table 4 Motors values

From these values, it was possible to develop a linear model of the motors by plotting the data and finding the equation that describes the model. For example, Fig. 11 describes the linearization of the RPM vs Thrust force.

Fig. 11

Linearization—RPM vs thrust

8 Mathematical approach—simulation

Based on the mathematical model, it was possible to build the sub-plants corresponding to $H_{\phi }$, $H_{\theta }$ and $H_{\psi }$ of the system. Each sub-plant and all the variables of the model were modeled on Simulink/MATLAB. The test consisted of analysis of the system’s response to a step signal as the input parameter. From Fig. 12, it is possible to notice the unstable behavior of the plants for this controlled input. For that reason, the design of a control system is required.

Fig. 12

System plants: roll $\phi$—pitch $\theta$—yaw $\psi$

8.1 Simulation—control design

The design of the controller for the plants described above was based on the theory of poles placement described by Phillips [27].Therefore, after a review on the literature on flying platforms [7, 24], it was needed to set some base parameters for the controller as the starting point:

• Tolerance of the system: 2%.

• Maximum overshooting 4.32% $\rightarrow \zeta = 0.707$.

• Setting time $Ts = 0.8~s$.

• Natural frequency: 7.2453

From those parameters, the poles $P_{1,2} = -5 \pm j~5.2434$ were obtained. As well as the desired plant.

$$\begin{aligned} H_{d} = \frac{52.49}{s^{2}+10~s+52.44} \end{aligned}$$

(26)

By observing the structure of the plants described by Eq. 26, it is possible to find some similarities on the structure of the system with respect to the orbital satellites plants.¹⁰ For that reason and taking advantage of the theories applied to the satellite plants, the first approach for the quadcopter’s controller was set like a Proportional-Derivative [28].

$$\begin{aligned} H_{PID} = Kp + \frac{Ki}{s} + Kd~s \end{aligned}$$

(27)

Modeling the system as Fig. 13, the general transfer function is defined by Eq. 28.

$$\begin{aligned} Hs = \frac{C~H}{1+C~H} \end{aligned}$$

(28)

Fig. 13

Standard control loop—unitary feedback

To find the parameters of the controller, it is necessary to follow the following steps:

• Replace C with the transfer function given by Eq. 27

• Replace H with the equation of the system on Laplace form seeing on Eq. 25

• Match and solve the resulting equation system to the desired plant given by Eq. 26

Table 5 Simulation control parameters

Fig. 14

System controlled plants: roll $\phi$—pitch $\theta$—yaw $\psi$

Taking Eq. 26 as the base of the model and using the transfer function for a PID controller given by Eq. 27, it was possible to find the controller values and represent them in Table 5.

From Fig. 14, it is possible to observe the response of each sub-plant with their controllers to a step signal. The behavior described shows a short stabilization time, needed for a flying platform. From Figure 14a,b and c, we observe a maximum overshooting lower than the 25% of its stationary value, which means that the behavior of the controller could be categorized as an aggressive controller, just as expected. The mean setting time of the controllers is around 1.3 S, which is acceptable for our purposes.

9 Design of the control system—application

For quadcopter controller systems, it is important to consider how robust the system should be regarding external forces like the wind or collisions. Normally, the force induced by the wind could be either constant or variable (gradual or not). For that reason, it is important to take into consideration how fast is the reaction of the quadcopter regarding external forces acting in a short time’s period.

Our proposed quadcopter’s controller design is divided into two sections. One in charge of the angle stabilization and the second in charge of the rate stabilization. The main reason for this configuration is to consider the deviation of the angle and rate of the desired position.

The first controller is in charge of the stabilization of the angle. The idea behind is to have a controller as faster as possible and stable. For this purpose, a P controller, see Fig. 15, is implemented.

Fig. 15

Stabilize P controller

The reference signal for the controller is given by the pilot (or a function) and it is considered the desired angle of movement based on the quadcopter coordinate system. The feedback input is given by the sensors, in this case, the input feedback value is the actual angle of the quadcopter. The output will be considered as the desired rotational rate, which will be the input for the next part of the controlling system.

The next step is to make the system stable against external forces. For this reason, the variations in the rotational speed of the quadcopter are considered in order to compensate for undesired changes (gradual or not). A PID controller is chosen due to the advantages given by the integral and derivative parts and simplicity in the future code implementation, see Fig. 16. The set input of this controller is the direct output of the stability controller.

Fig. 16

Rate PID controller

The goal is to rotate the quadcopter in a particular rate (given by degrees per second) in any of the possible directions (roll $\phi$, pitch $\theta$, yaw $\psi$). The feedback input is given directly from the sensors. This implementation requires that the feedback input would be in degrees per second as to match the desired rotational rate which has that unit. The output of the controller is directly sent to the motors.

The whole controller, Fig. 17, is the composition of the stability and rate controller in cascade mode (one branch per angle). The idea behind consists that when the first controller reaches the desired angle, its output will be zero; thus, the input for the rate controller will be zero and the quadcopter will not have a rotational movement. On the other hand, when the difference of the first controller with respect to the control signal is not zero, the second controller will have a nonzero input and the quadcopter will have a rotational movement.

Fig. 17

Quadcopter controller per angle

For the complete implementation of the controller, it was used as a parallel controller configuration as shown in Fig. 18. There it was possible to process the corresponding data from Roll, Pitch and Yaw simultaneously, as well as height when it was required.

Fig. 18

Quadcopter controller

10 Implementation of the control system

10.1 Determining orientation

Accelerometers and gyroscopes are the sensors used for determining the orientation. The first one measures acceleration in each direction of the coordinate system (xyz), and the second one measures angular velocity. Based on the specification of our IMU [9], the accelerometers tend to be very sensitive to vibrations and their reaction time is not so fast as gyroscopes. Gyroscopes tend to be vibration resistant but turn to drift some degrees with the pass of time. For this implementation, a fusion of the data collected by both sensors will help us to determinate the accurate position orientation of the quadcopter.

10.2 Acrobatic/rate mode control

The stabilize controller (Fig. 15) requires the implementation of a P controller, while the rate controller (Fig. 16) requires a PID controller. Either the P or the PID controller, both share the same code structure. The difference is given by the controller parameters, where kp, ki and kd define the type of controller (P-PI-PD-PID).

10.3 Controller—tuning

When the radio controller (or a specific preset function) gives the order to rotate to a particular rate, thmode controle quadcopter should respond faster and as precise as possible. The first approach to the controller values was given by the simulation of the system (see Sect. 8.1). However, manual calibration of the controller values was required to tune the controller and obtain the desired behavior of the system.

In order to tune the controllers, it was implemented a function capable to change the PID values through RS232 communication. Basically, the PID parameters are displayed on the PC screen and it is possible to send a command (hexadecimal numbers) to the quadcopter(due to RS232 communication) in order to manipulate the parameters in real time.

The tuning process can be described by Fig. 19

Fig. 19

PID values—tuning process

The chosen PID values described in Table 6 refers to the final values after the tuning process was done.

Table 6 PID Controller values

10.4 Programming structure

The program code is divided in five sections, see Fig. 20.

Fig. 20

Main program structure

• 1. Stand-by mode This part is active when the quadcopter is turned on. It has a security function which allows you to ’arm’ or ’disarm’ the quadcopter. Those states are changed by a combination given by the R/C controller.

• 2. Values This section corresponds to the acquisition block of data from the sensors and the commander, as well as the selection of the flight mode by using the switches on the radio controller. The data acquisition from the sensors is done by using interruption methods on the $\mu C$ at a fixed time cycle. Regarding the inputs from the commander, two main functions are stated. Set acquire and Set values are the corresponding functions to get the data from the R/C controller or the commander that will be used as the reference data for our controllers. Basically, here is where the information of movement set by the pilot is taken by the quadcopter.

• 3. PID Seven individual PIDs are set in this section. On this section, the data acquired on the values section would be the input data on each of the seven controllers. Each of the controller branches states in this section will deliver an output corresponding to the three reference angles and the height of the quadcopter respectively.

  Roll	Set-angle	Rate
  Pitch	Set-angle	Rate
  Yaw	Set-angle	Rate
  Height	Hold-Z	-

• 4. Mixers The total thrust of the motor will be the combination of the power exerted by the throttle, pitch, roll and yaw together in one single output per signal. Therefore, all the processed data should be mixed into one single value characterized for each one of the four motors. The data are set in a matrix 4x4 like the one described by Eq. (29), and the final value is given directly to the ’output’ section.

  $$\begin{aligned} \begin{pmatrix} m_{1} \\ m_{2} \\ m_{3} \\ m_{4} \end{pmatrix} = \begin{pmatrix} Thro[x] + Pitch[x] + Roll[x] - Yaw[x] \\ Thro[x] + Pitch[x] - Roll[x] - Yaw[x] \\ Thro[x] + Pitch[x] - Roll[x] - Yaw[x] \\ Thro[x] + Pitch[x] + Roll[x] + Yaw[x] \\ \end{pmatrix} \end{aligned}$$

  (29)

• 5. Output Finally, the data given by the mixer is processed to build a PWM signal¹¹ for each of the channels of the motors. Each of these signals is sent to the respective motor drivers in order to activate the movement on the corresponding motors.

Additional information about the program code.

• The maximum main loop time is $76.8~{\upmu {\mathrm{s}}}$. This occurs when all the functions are executed.

• The minimum main loop time is $1.92~{\upmu {\mathrm{s}}}$. This occurs when the IMU is not ready to send data and the program skips the PID, mixers and output sections.

• If the peripheral LCD is writing every cycle of the main loop, the main loop time will increase up to 47.6 ms.

11 Experimental results

To make possible the calibration of the whole system, it was necessary to fix the quadcopter into a test platform. Three versions of this platform were used to test the flying controller. The first version consisted on a string attached along the x- or y-axis, allowing the quadcopter to move in 1DOF, pitch or roll, respectively, see Fig. 21. The second platform consisted on the quadcopter attached with strings from the main body on the z-axis, see Fig. 22. This allow us to test the yaw controller and give more freedom to the pitch and roll controller for test. The third platform consisted on a special 3D printed structure attached to the under section of the body frame of the quadrotor, see Fig. 23. This one allows the quadcopter to move in 6DOF under certain restrictions.

Fig. 21

First flying test platform

Fig. 22

Second flying test platform

Fig. 23

Third flying test platform

Fig. 24

Sequence of video frames: control test in a controlled environment

The quantitative collection of data corresponding to the sensors in the quadcopter was not possible when carrying out the test flights due to limitations in the measurement equipment.¹² One of the wire-line procedures for the data collection was normally collected using a connection cable between the test platform and the base station. The addition of this connection cable with the necessary length to cover a working radius equal to the working range of the control command would significantly modify the dynamic model of the platform, harming the behavior of the implemented control system.

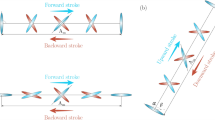
It was possible to study the stability of the quadcopter by using video frames as reference points by using camera recording at 60 frames per second. Figure 24 shows a series of video frames¹³ of one of the stability controller’s test. Figure 24 shows a white axis aligned along the M2 and M4 arms of the quadrotor frame (see Fig. 2) that works as a reference axis to study the overall stability of the quadcopter on the photo frames. This test was performed in a variation of the first test platform. In the sequence of images, the behavior of the system on the exposure to external disturbances is observed. On the video frames, it is possible to observe how the quadcopter finds stability in a approximately 2.2 s (in average 135 video frames, at 60 frames per seconds) after being exposed to an external force.

As a general conclusion, we can state that when using variables based on qualitative methods as a stability reference, the quadcopter proved to be stable for both indoor and outdoor flights, as well as a fast and stable reaction to external forces applied to the system.

12 Conclusion

We present a theoretical model for a quadcopter-type UAV to answer the question of ’How to implement an attitude controller on a quadcopter for indoor and outdoor flights as a step forward to support the safety features in factory applications’. Based on this model and after tuning the values based on empirical tests on safe-controlled environments, the stability of the real prototype was tested for free flights both in interior and exterior environments. On the development of the research phase, theoretical and empirical methods were implemented. These approaches were fundamentals as to show the direct relationship between the theoretical model and the behavior “change-result” given by the empirical approach; therefore, the obtained experimental results were proven to match with the studied theories.

Due to the simplifications considered in the model, the design of the controller was divided into two phases: the theoretical phase, corresponding to the mathematical model and design of the controller, and the actual implementation of the theories on the physical model. The theoretical model was used for the estimation of the dynamics of the quadcopter and the approximation of a theoretical control system, while in the experimental phase, it was proved that the theoretical simplifications resulted in the development of a plant that did not fulfill all the characteristics of the real system, so it was necessary an experimental adjustment in the parameters of the controllers.

In outdoor flights, the quadcopter deviated from its original position due to the influence of the air currents present; however, this could be controlled manually by the pilot. It is suggested the future addition of a satellite position controller to avoid the deviation of position by the wind while using the built-in GPS module mounted on the quadcopter. However, the system remains stable for rolling $\phi$, pitching $\theta$, yawing $\psi$ angles, as well as against the influence of wind and other external forces.

Although it is true that the possible implementation of these flying platforms in the industries could bring substantial benefits, it is still in its early stages of research. The UAV systems would be strong allies in the development of the industries in the future; however, the limitation of this implementation depends on the lack of trustful application on large-scale and commercial use, as well as the restrictions in the legal framework on the countries for the use of drones at outdoor and/or indoor environments. Additionally, it will be needed to break the paradigm of the traditional methods used on certain operations in the industries like patrolling, inspections, transportation and other; and incorporate robots as our allies to develop those tasks.

Existent aerial regulations have to be replaced or renovated and new ones have to be implemented in order to progress with the implementation of drones in the daily industrial activities. According to the information provided by the agency EASA, a new regulation¹⁴ based on the results of the previous EASA’s cases of study developed since 2016 has been introduced in February 2018 to the European Commission. It is expected to have an answer on this matter at the end of 2018, thus these regulations could be fully implemented at the beginning of 2019.

Future works extend in several directions. The controller presented here was based on the Newton–Euler equations; however, the analysis of this system could have been done also by implementing the Lagrangian equations. This will derive in an equivalent controller system that might lead to others cases of study on the comparison of both controllers in a real-life application. Another approach is to design the controller without major simplifications as the ones taken on this paper. Thus, the dynamics of the system would be more complex as well as the controller. Further works will study the statement of the problem covered in this paper by applying different controller’s configuration, i.e., fuzzy logic, nonlinear control, neural networks, adaptive, etc.