A Cautionary Note on Evidence-Accumulation Models of Response Inhibition in the Stop-Signal Paradigm

Abstract

The stop-signal paradigm is a popular procedure to investigate response inhibition—the ability to stop ongoing responses. It consists of a choice response time (RT) task that is occasionally interrupted by a stop stimulus signaling participants to withhold their response. Performance in the stop-signal paradigm is often formalized as race between a set of go runners triggered by the choice stimulus and a stop runner triggered by the stop signal. We investigated whether evidence-accumulation processes, which have been widely used in choice RT analysis, can serve as the runners in the stop-signal race model and support the estimation of psychologically meaningful parameters. We examined two types of the evidence-accumulation architectures: the racing Wald model (Logan et al. 2014) and a novel proposal based on the lognormal race (Heathcote and Love 2012). Using a series of simulation studies and fits to empirical data, we found that these models are not measurement models in the sense that the data-generating parameters cannot be recovered in realistic experimental designs.

Models of Response Inhibition in the Stop-Signal Paradigm

Response inhibition is the ability to stop responses that are in progress but become no longer appropriate—such as stopping when the traffic light turns red. As a central component of executive control (Aron et al. 2014; Logan 1994; Miyake et al. 2000; Ridderinkhof et al. 2004), response inhibition has profound impact on daily functioning and ensures that people can safely interact with their world. Failures of response inhibition can result in adverse outcomes and are also considered integral to various neurological and psychiatric disorders (e.g., Badcock et al. 2002; Schachar et al. 2000).

In the laboratory, response inhibition is often investigated using the stop-signal paradigm (Logan and Cowan 1984; for a recent review, see Matzke et al. 2018), typically based on a two-choice response time task (e.g., pressing left button for a left arrow, or right button for a right arrow). On a minority of trials, this primary “go” task is interrupted by a stop signal, at a variable delay (“stop-signal delay” or SSD), instructing participants to withhold their response. Response inhibition succeeds when the stop signal comes soon enough after the onset of the go stimulus but fails when it comes later—too close to the moment of response execution. The stop-signal paradigm has been used in numerous studies, with both healthy and clinical populations, to examine the cognitive, developmental, and neural underpinning of response inhibition (e.g., Aron and Poldrack 2006; Badcock et al. 2002; Bissett and Logan 2011; Fillmore et al. 2002; Forstmann et al. 2012; Hughes et al. 2012; Matzke et al. 2017a; Schachar et al. 2000; Schachar and Logan 1990; Verbruggen et al. 2014; Williams et al. 1999).

Performance in the stop-signal paradigm is commonly formalized as a race between two runners representing independent cognitive processes: a single go process that is triggered by the go stimulus and a stop process that is triggered by the stop signal (Logan 1981; Logan and Cowan 1984). According to the stop-signal race model, the outcome of response inhibition depends on the relative finishing times of the go and stop processes. If the stop process wins, the go response is successfully inhibited; if the go process wins, the go response is executed. The model does not require the specification of the parametric form of the finishing times of the go and the stop process and makes distribution-free predictions about the interplay of response times (RTs) and inhibition rates.

The stop-signal race model plays a central role in response inhibition research because it enables the non-parametric estimation of the unobservable latency of the stop response, known as the stop-signal reaction time (SSRT; Colonius 1990; de Jong et al. 1990; Logan and Cowan 1984; for an overview, see Matzke et al. 2018). Reliable non-parametric estimates of SSRT can be obtained with as few as 50 stop-signal trials per participant (Verbruggen et al. 2019).

Although the non-parametric approach theoretically provides estimates of (upper limits on the) moments of the entire SSRT distribution, non-parametric estimation of moments higher than the mean requires an unrealistically large number of stop-signal trials (Logan 1994; Matzke et al. 2013). To address this limitation, Matzke et al. (2013, 2017b) developed the BEESTS approach that parameterizes the finishing time distribution of the go and stop processes using an ex-Gaussian distribution. BEESTS provides a reliable characterization of the entire SSRT distribution based ∼50 stop-signal trials per participant when implemented in a hierarchical framework (Matzke et al. 2017b).

Both approaches, the traditional non-parametric and parametric BEESTS approaches are purely descriptive: They allow researchers to quantify the latency of stopping and describe differences in stop-signal performance between individuals or experimental conditions. Descriptive models, however, do not explain performance, and can, therefore, sometimes fail to give direct insights into the cognitive processes that contribute to successful stopping.

More recently, Matzke et al. (2019) extended the BEESTS approach to also model the choice embedded in the go task by including one go runner for each response option as well as a stop runner, all with finishing times described by ex-Gaussian distributions. This approach provides a process account of the choice errors in terms of which go runner wins the race, but contrary to process models of choice RT (Brown and Heathcote 2008; Vickers 1979), the ex-Gaussian finishing times of the runners do not have a plausible psychological interpretation in terms of an evidence-accumulation process. In particular, the mapping between the parameters of the ex-Gaussian distribution and the parameters of evidence-accumulation processes can be difficult to specify (Matzke and Wagenmakers 2009), and so the three-runner model proposed by Matzke et al. has difficulty realizing the benefits of a full process model.

To illustrate the limitations of using a distribution like the ex-Gaussian to describe finishing times, even if it is sufficiently flexible to do so quite accurately, consider Matzke et al.’s (2017a) findings about stop-signal performance deficits in schizophrenia. They augmented the BEESTS approach with the ability to account for “trigger failures,” occasions on which the stop runner fails to enter the race. They found that apparent inhibitory deficits in patients were largely due to trigger failures, which they attributed to deficits in attention rather than inhibition. However, there was also a uniform slowing in the SSRT distribution, as quantified by the ex-Gaussian μ parameter. This slowing could result from the same attention deficit that is responsible for trigger failures also causing a delay in the time at which the stop runner entered the race, but it could also result from a slowing in the speed of the rate at which it races, which would be more consistent with an inhibitory deficit. Matzke et al. argued for the former account because slowing in patients’ go RT distributions was due to an increase in skew as quantified by the ex-Gaussian τ parameter rather than a μ effect as was found for SSRT. However, this inference required assumptions based on findings about the general nature of slowing in evidence accumulation in schizophrenia (Heathcote et al. 2015b) and on partial mappings between the ex-Gaussian and evidence-accumulation parameters identified by Matzke and Wagenmakers (2009). A much more straightforward conclusion would have been possible if the runners had been modeled by evidence-accumulation processes, because their parameters separate factors determining the time taken to run the race (i.e., the rate of accumulation and the amount of evidence required to make a choice) and factors related to when the runners enter the race.

Stop-Signal Evidence-Accumulation Models

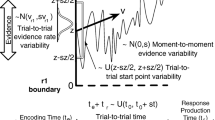
Logan et al. (2014) proposed an evidence-accumulation model of response inhibition that provides a comprehensive process characterization of stop-signal performance. The model assumes an independent race among a set of runners, each characterized as a single-boundary diffusion process where evidence accumulates stochastically at a constant average rate until a threshold is reached. As in Matzke et al. (2019), one runner corresponds to the stop response and each of the remaining runners corresponds to one of the N possible response options in the go task. The single-boundary diffusion process produces a Wald distribution (Wald 1947) of finishing times, which has an analytic likelihood, facilitating Bayesian and maximum-likelihood estimation of the model parameters. The Wald distribution is characterized by three parameters: rate of evidence accumulation, decision threshold, and non-decision time. The non-decision time parameter shifts the lower bound of the finishing time distributions to RTs greater than zero to account for the duration of processes involved in the encoding of the stimuli (e.g., the choice stimulus or the stop signal) and, for the go accumulators, the production of responses.

Logan et al. (2014) tested hypotheses about capacity limitations by comparing stop-signal performance over conditions requiring choices among different numbers of options (i.e., N), where they identified capacity with evidence-accumulation rates (see also Castro et al. 2019). Their analysis relied on data with exceedingly low measurement noise, with 6480 go and 2160 stop-signal trials per participant and compared the maximum-likelihood fit of models in which capacity was unlimited (i.e., rates did not vary with N) or limited (i.e., different rates were estimated for each N) for both the go processes and the stop process. Model selection based on the Bayesian information criterion (BIC; Raftery 1995; Schwarz 1978) favored the model with limited capacity for the go process but unlimited capacity for the stop process (i.e., the same stop rate for different N). As the sum of rate parameters for the go processes decreased as N increased, Logan et al. inferred that the go process had limited capacity. These conclusions illustrate the advantages afforded by the evidence-accumulation framework in enabling direct tests of hypotheses about psychological processes that are not possible with descriptive stop-signal race models.

Challenges to Parameter Estimation

Parameter-dependent lower bounds are a necessary feature of any theoretically plausible RT model in general (Rouder 2005), and evidence-accumulation models in particular. However, they make estimation irregular, so that estimates based on likelihoods are not necessarily optimal (Cheng and Amin 1983). For instance, maximum-likelihood estimation can return the minimum observed RT as estimate of the lower bound parameter, and so it must necessarily overestimate the true lower bound. On average, the degree of overestimation increases as the number of trials and hence measurement precision decreases (for further discussion, see Heathcote and Brown 2004). Such irregularity is typically not problematic in evidence-accumulation models for standard choice tasks, but it may pose challenges to parameter estimation for the partially observed data available in the stop-signal paradigm. Indeed, Matzke et al. (2019) suggested that this was the case because they had little success in obtaining stable estimates for the stop-process parameters when applying Logan et al.’s (2014) evidence-accumulation model to their data with a realistic number of 395 go and 144 stop-signal trials per participant. In contrast, the ex-Gaussian stop-signal race model performed well with this data, even when made more complex by augmenting it with parameters to account for attention failures.

Our goal here is to understand why these estimation problems occurred, and how they generally apply, by investigating the estimation properties of stop-signal evidence-accumulation models as a function of the number of stop-signal trials. In particular, we examine whether stop-signal evidence-accumulation models can serve as measurement models. We define measurement models as models having a one-to-one mapping between the data-generating parameter values and the corresponding estimates, which enables the quantification of (differences in) the psychological processes represented by the model parameters. This property is crucial when researchers are interested in assessing individual differences in psychological processes and their relationship to covariates, or when they want to quantify the magnitude of differences between individuals, populations, or experimental conditions.¹

In measurement models, the unique mapping between generating and estimated parameters implies that fits to simulated data can be used to recover the data-generating parameters. Our investigation will, therefore, rely on a series of parameter-recovery studies (Heathcote et al. 2015a). We will use Bayesian parameter estimation to evaluate not only any bias in the estimates but also how well uncertainty about these estimates is quantified by the posterior distributions. A good assessment of uncertainty is highly desirable in order to ensure that researchers are not overly confident in their inferences about parameters.

We performed this investigation not only using Logan et al.’s (2014) racing Wald model but also a novel proposal based on the lognormal race (Heathcote and Love 2012; Rouder et al. 2015). The lognormal race model belongs to the family of evidence-accumulation models with a parameter-dependent lower bound, and as such it constitutes a process-plausible conceptualization of performance. The lognormal race, in contrast to the Wald model, cannot separately identify evidence-accumulation rates and decision thresholds. This may be disadvantageous for answering some research questions, such as Logan et al.’s specific question about evidence-accumulation rates, but not others, such as the question examined by Matzke et al. (2017a) about group differences in the time the stop runner enters the race. Although less psychologically informative, the lognormal race model has better estimation properties than the Wald, and this may be particularly beneficial in the context of stop-signal data.

In what follows, we first provide a formal introduction to the general stop-signal race architecture and present the lognormal and Wald evidence-accumulation instantiations of the framework. We then discuss the results of a series of parameter-recovery studies, followed by an empirical validation of our findings.

Race Models for the Stop-Signal Paradigm

Stop-signal race models predict that the probability of go response i, i = 1, ⋯, N is given by the probability that go process i finishes before all other racers (see also Logan et al. 2014; Matzke et al. 2018):

$$ {P}_{R,i}\left({t}_{\mathrm{ssd}}\right)={\int}_0^{\infty }{f}_{\mathrm{go},i}(t)\prod \limits_{j\in N}^{j\ne i}\left(1-{F}_{\mathrm{go},j}(t)\right)\left(1-{F}_{\mathrm{stop}}\left(t-{t}_{\mathrm{ssd}}\right)\right) dt, $$

(1)

where f_{go, i} is the probability density function (PDF) of the finishing times of go accumulator i and F_stop(t − t_ssd) is the cumulative distribution function (CDF) of the finishing times of the stop accumulator at stop-signal delay (SSD) t_ssd. On go trials, t_ssd = ∞ and F_stop(t − t_ssd) = 0. The probability of inhibition is given by

$$ {P}_I\left({t}_{\mathrm{ssd}}\right)={\int}_0^{\infty }{f}_{\mathrm{stop}}\left(t-{t}_{\mathrm{ssd}}\right)\prod \limits_{i\in N}\left(1-{F}_{\mathrm{go},i}(t)\right) dt, $$

(2)

and the conditional PDF of RTs given that the response was not inhibited is then

$$ {f}_i\left(t|{t}_{\mathrm{ssd}}\right)=\frac{f_{\mathrm{go},i}(t){\prod}_{j\in N}^{j\ne i}\left(1-{F}_{\mathrm{go},j}(t)\right)\left(1-{F}_{\mathrm{stop}}\left(t-{t}_{\mathrm{ssd}}\right)\right)}{1-{P}_I\left({t}_{\mathrm{ssd}}\right)}. $$

(3)

On go trials, F_stop(t − t_ssd) = 0 and P_I(t_ssd) = 0. Note that on stop-signal trials, t_ssd <  < ∞ and Eq. 3 is the PDF of RTs for response i that escaped inhibition, also known as signal-respond RTs.

The PDF of RTs on go trials is given by

$$ {f}_{\mathrm{go}}(t)=\sum \limits_{i\in N}{f}_{\mathrm{go},i}(t)\prod \limits_{j\in N}^{j\ne i}\left(1-{F}_{\mathrm{go},j}(t)\right), $$

(4)

and the PDF of signal-respond RTs is given by

$$ {f}_{SR}\left(t|{t}_{\mathrm{ssd}}\right)=\frac{\sum_{i\in N}{f}_{\mathrm{go},i}(t){\prod}_{j\in N}^{j\ne i}\left(1-{F}_{\mathrm{go},j}(t)\right)\left(1-{F}_{\mathrm{stop}}\left(t-{t}_{\mathrm{ssd}}\right)\right)}{1-{P}_I\left({t}_{\mathrm{ssd}}\right)}. $$

(5)

Stop-Signal Lognormal Race Model

The lognormal distribution has a long history in modeling simple and choice RTs due to its desirable measurement properties and excellent fit to empirical RT distributions (e.g., Ratcliff and Murdock 1976; Ulrich and Miller 1994; Woodworth and Schlosberg 1954). Here we build on Heathcote and Love’s (2012) lognormal race model (see also Rouder et al. 2015) and embed the lognormal distribution in the stop-signal race architecture. We denote the resulting model as the stop-signal lognormal race model (SS-LNR).

The time to accumulate evidence to a threshold has a lognormal distribution when one or both of either the rate of accumulation or the distance from start-point to threshold have a lognormal distribution. Hence, each of N such go accumulators in the race has a lognormal distribution with parameters μ (location) and σ (σ > 0; scale). The PDF of the finishing time distribution of go accumulator i, i = 1, ⋯, N, is thus given by

$$ {f}_i(t)=\frac{1}{t\sigma \sqrt{2\pi }}\exp\ \left(-\frac{1}{2}{\left(\frac{\ln (t)-\mu }{\sigma}\right)}^2\right),\mathrm{for}\ t>0. $$

(6)

The PDF of the finishing time distribution of the stop accumulator with support t > t_ssd can be obtained by substituting (t − t_ssd) for t, and μ_Stop and σ_Stop for μ and σ in Eq. 6. The finishing time distribution of the winner of the race is given by the distribution of the minima of the lognormal distributions for all the runners. It is clear from Eq. 6 that the SS-LNR cannot separately identify decision thresholds and evidence-accumulation rates; only the ratio of thresholds-to-rate is identifiable. Our software implementation of the SS-LNR is available at https://osf.io/rkw5a/ as part of the Dynamic Models of Choice collection of R functions and tutorials (Heathcote et al. 2019).

Although suppressed in Eq. 6, the SS-LNR assumes that the finishing time distributions have a parameter-dependent lower bound that shifts the distribution away from zero. As in standard evidence-accumulation models, the parameter-dependent lower bound of the go accumulator quantifies non-decision time t_g, the duration of processes outside the decision-making process. Note that t_g has two components, the time to encode the go signal and the time to produce a response once the go process finishes, but these cannot be separately identified. For the stop accumulator, the psychological interpretation of this parameter, which we denote C, depends on the assumptions about when go response production can be interrupted once it has reached its threshold. If go response production is assumed to be entirely non-ballistic (i.e., the go response can be stopped right up to the instant that it occurs), C retains the standard interpretation of non-decision time as the duration of processes outside the decision-making process. However, if go response production is assumed to be ballistic, either fully (i.e., the go response cannot be stopped once it has reached threshold) or partially (i.e., it can be stopped after it has reached threshold but not right up to the instant it occurs), C lumps together the non-decision component of the stop process and the ballistic response production component of the go process. The reader is referred to Logan and Cowan (1984) for the non-parametric treatment of the role of ballistic processes in stopping and to the Supplemental Materials (https://osf.io/rkw5a/) for the derivations in the context of the evidence-accumulation framework.

Stop-Signal Racing Wald Model

The Wald distribution (i.e., inverse Gaussian distribution; Wald 1947) represents the density of the first passage times of a Wiener diffusion process toward a single absorbing boundary. The Wald has a rich history in the RT literature (e.g., Burbeck and Luce 1982; Emerson 1970; Luce 1986; Heathcote 2004; Schwarz 2001; Schwarz 2002; Smith 1995), and has been recently embedded in the racing evidence-accumulation architecture for modeling choice RTs (Leite and Ratcliff 2010; Teodorescu and Usher 2013). Logan et al. (2014) derived closed form solutions for the likelihood of the racing Wald model and applied it to the stop-signal paradigm.

The resulting stop-signal racing Wald model (SS-RW) assumes that the stop accumulator and each of the N go accumulators is a Wiener diffusion process with evidence-accumulation rate v (v > 0), start point 0, and threshold k (k > 0). The model allows thus for the separation of thresholds and rates. The finishing time distribution of each accumulator is a Wald distribution. Hence, the PDF of the finishing time distribution of go accumulator i, i = 1, ⋯, N, is given by

$$ {f}_i(t)={k}_i{\left(2\pi {t}^3\right)}^{-\frac{1}{2}}\exp\ \left(-\frac{1}{2t}{\left({v}_it-{k}_i\right)}^2\right),\mathrm{for}\ t>0. $$

(7)

The PDF of the finishing time distribution of the stop accumulator with support t > t_ssd is obtained by substituting (t − t_ssd) for t, and v_Stop and k_Stop for v and k in Eq. 7. The finishing time distribution of the winner of the race is given by the distribution of the minima of the Wald distributions for all the runners. The SS-RW also assumes a parameter-dependent lower bound for each accumulator, t_g for the go accumulators and C for the stop accumulator, and a drift coefficient that we set to 1 to make the model identifiable (Donkin et al. 2009).

To account for fast error RTs, Logan et al. (2014) extended the SS-RW to allow for uniform trial-by-trial variability in response threshold, with support [(k − a), (k + a)]. In the full model, the PDF of the finishing time distribution of go accumulator i is given by

$$ {g}_i\left(t|{v}_i,{k}_i,{a}_i\right)=\frac{1}{2{a}_i}\left(\phi \left({\alpha}_i\right)-\phi \left({\beta}_i\right)-{v}_i\left(\Phi \left({\alpha}_i\right)-\Phi \left({\beta}_i\right)\right)\right),\mathrm{for}\ {v}_i>0,{a}_i>0, $$

(8)

where

$$ \alpha =\frac{-\left(k-a- tv\right)}{\sqrt{t}}, $$

(9)

and

$$ \beta =\frac{\left(k+a- tv\right)}{\sqrt{t}}, $$

(10)

and ϕ(x) and Φ(x) are the PDF and CDF of the standard normal distribution, respectively. Note that for a = 0, Eq. 8 simplifies to Eq. 7.

Equations 7–10 follow Logan et al.’s (2014) notation in terms of threshold k and threshold variability a. Our simulations will rely on a slightly different parameterization in terms of threshold b (b > 0) and start-point variability A, where A is assumed to be uniformly distributed from 0-A, and the “threshold gap” is given by B = b − A (B >  = 0). Hence, k = b − A/2 = B + A/2 and a = A/2. The new parametrization allows us to enforce b > A by assigning a positive prior distribution to B. Our software implementation of the SS-RW is available at https://osf.io/rkw5a/.

Parameter-Recovery Studies

We report the results of a series of parameter-recovery studies aimed at investigating the measurement properties of the SS-LNR and the SS-RW as a function of the number of stop-signal trials. In particular, we examined four scenarios: 300 go and 100 stop, 600 go and 200 stop, 1200 go and 400 stop, and 9600 go and 3200 stop trials. The first scenario is representative for clinical/developmental studies, the second and third for experimental investigations, and the fourth can be practically considered as a near-asymptotic case with substantially more trials than Logan et al.’s (2014) design with extremely low measurement noise. In each recovery study and for each sample-size scenario, we generated 200 synthetic data sets with the same true value. The true values were chosen to result in realistic go RT and SSRT distributions by cross-fitting ex-Gaussian go RT and SSRT distributions reported in Matzke et al. (2019) with the lognormal and the Wald distributions.² Unless indicated otherwise, SSD was set using the staircase-tracking algorithm (e.g., Logan 1994); SSD was increased by 0.05 s after successful inhibitions and was decreased by 0.05 s after failed inhibitions.

As the parameters of both models are strongly correlated, we used the Differential Evolution Markov Chain Monte Carlo (DE-MCMC; Ter Braak 2006; Turner et al. 2013) algorithm to sample from the posterior distribution of the parameters. The reader is referred to the Supplemental Materials for a more detailed explanation of MCMC-based Bayesian inference (Figure S1). We set the number of MCMC chains to three times the number of model parameters and initialized each chain using over-dispersed start values. The MCMC chains were thinned as appropriate to reduce auto-correlation. During the burn-in period, the probability of a migration step was set to 5%; after burn-in, only crossover steps were performed until the chains converged to their stationary distribution. Convergence was assessed using the following procedure. Apart from monitoring the proportional scale reduction factor ($\hat{R}$) to ascertain that the MCMC chains have mixed well (Brooks and Gelman 1998; Gelman and Rubin 1992; criterion: $\hat{R}<1.1\Big)$, we assessed the stationarity of the chains by (1) treating the first and second half of a chain as a different chain when calculating $\hat{R}$; (2) monitoring the absolute change in the median between the first and last third of the posterior samples relative to the interquantile range (criterion: <0.5); and (3) monitoring the absolute change in the interquantile range between the first and last third of the posterior samples relative to the overall interquantile range (criterion: <0.5). This procedure was followed by visual inspection of the MCMC chains.

Unless indicated otherwise, we used wide uninformative uniform prior distributions (see Supplemental Materials) in order to avoid posterior distributions that are truncated by the—arbitrary—lower or upper bound of the priors. This allowed us to maintain the structural correlations among the model parameters (as reflected in the pairwise correlations among the posterior samples), which in turn enabled us to thoroughly explore the behavior of the models.

To assess the bias of the parameter estimates, we computed the median of the means of the posterior distributions across the 200 replications and compared it to the true value. To assess the uncertainty of the estimates, we computed the median of the lower and upper bounds of the central 95% credible intervals. The 95% credible interval (CI) quantifies the range within which the true data-generating parameter value lies with 95% probability (see Morey et al. 2016, for a discussion of the differences between Bayesian credible intervals and frequentist confidence intervals). To assess the calibration of the posterior distributions, we computed the percentage of replications for which the CI contained the true value (i.e., coverage) and determined whether estimates fall within the CI at the nominal rate.

Stop-Signal Lognormal Race Model

We present parameter-recovery results for a standard two-choice stop-signal design featuring only a stimulus factor (e.g., right or left arrow) assuming the following go parameters: μ_T and μ_F for the location parameter of the go runner that matches and mis-matches the stimulus, respectively, σ_T and σ_F for the matching and mis-matching scale parameters, and non-decision time t_g. For the stop accumulator, we assumed μ_Stop, σ_Stop, and C. The first two panels in the top row of Fig. 1 show the true data-generating go RT and SSRT distributions.

Fig. 1

True and predicted RT distributions for the SS-LNR. For the go RT distribution, the black density line corresponds to correct RTs and the red density line corresponds to error RTs

Figure 2 shows parameter recovery as a function of the number of go and stop-signal trials. The Supplemental Materials show detailed results, including the distribution of the posterior means and representative posterior distributions for the scenarios with 200 and 3200 stop-signal trials (Figure S2). The Appendix in the Supplemental Materials provides examples of the MCMC chains.

Fig. 2

Parameter recovery for the SS-LNR as a function of the number of go and stop-signal trials. The horizontal dotted lines indicate the true values. The black bullets show the median of the posterior means across the 200 replications. The error bars show the median width of the central 95% CIs across the replications. The percentages indicate the coverage of the 95% CIs. The ranges of the y-axes correspond to the ranges of the uniform prior distributions on the model parameters

The recovery of the go parameters is excellent: the parameter estimates closely approximate the true values, and the coverage of the 95% CIs is close to nominal, even with relatively few go trials. As expected, as the number of go trials increases, the uncertainty of the estimates decreases. In contrast to the go estimates, the stop estimates are heavily biased unless a very large number of stop-signal trials are available. In particular, the μ_Stop parameter is underestimated, whereas σ_Stop and C are overestimated. The coverage of the 95% CIs is far below nominal, even in the near-asymptotic case of 3200 stop-signal trials. For μ_Stop and σ_Stop, the uncertainly of the estimates decreases as the number of stop-signal trials increases, and the same is true for C for larger sample sizes. Note, however, that the posterior distribution of C is very wide even with 3200 stop-signal trials, indicating substantial uncertainty in estimating this parameter. Note also that—contrary to the other three sample sizes—the posterior of C is quite narrow in the 100 stop-trial scenario, conveying a false sense of confidence in the biased estimates in small samples. This pattern probably arose from the combination of the strong bias and the strong structural correlations between the stop parameters, which imposed an implicit upper bound on C.

In the Supplemental Materials, we present parameter recoveries for a more complex design that features the manipulation of the stop parameters, and explore the effects of using fixed SSDs, high-accuracy paradigms, and informative prior distributions (Figures S3–S5). The results show similar performance as reported in the main text, indicating that poor parameter recovery is not unique to the particular design used in our simulations and is not necessarily improved by imposing highly informative prior distributions.

The third panel in the top row and the second row of Fig. 1 show predicted SSRT distributions that were generated using the median of the posterior means of the biased stop estimates for the four sample-size scenarios. For realistic samples sizes, the predicted SSRT distributions are more peaked than the true SSRT distribution (middle panel in the top row of Fig. 1), with an unrealistically steep leading edge. This pattern suggests a trade-off between the estimated variance and the lower bound C of the finishing time distribution of the stop accumulator. In fact, in the 100 stop-trial scenario, the predicted SSRT distribution has near-zero variance and its mode closely approximates the lower bound C, which is relatively close to the mode of the true SSRT distribution (estimated C = 0.313, estimated mode =0.313, and true mode =0.309).³

These results imply that parameter recovery can be adequate when the true SSRT distribution has very low variance. This is illustrated in Fig. 3 where we compare recovery performance for a SSRT distribution with appreciable variance and one with near-zero variance. The black density lines (right panels) and histograms (left panels) show the 200 posterior distributions and the distribution of the corresponding 200 posterior means, respectively, for the recovery study with 100 stop-signal trials using the distribution shown in the middle panel in the top row of Fig. 1 as the data generating SSRT distribution. Note that the same results are also summarized in Fig. 2. The black triangles show the true values and the gray triangles show the median of the posterior means across the 200 replications. As established earlier, the parameter estimates are heavily biased. The gray density lines and histograms show the results of a new recovery study where we used a distribution with near-zero variance shown in the first panel in the second row of Fig. 1 as the data-generating SSRT distribution. In the new simulation, the true values equal the biased estimates from the first recovery study depicted by the gray triangles. As shown in Fig. 3, recovery performance in the new parameter region is satisfactory, in terms of both bias and coverage.

Fig. 3

Misleading parameter recovery for the SS-LNR. The black density lines and histograms show the 200 posterior distributions and the distribution of the corresponding 200 posterior means, respectively, from the parameter-recovery study with 100 stop-signal trials generated by the SSRT distribution in the middle panel in the top row of Fig. 1. The black triangles show the true values and the gray triangles show the median of the posterior means across the 200 replications. The gray density lines and histograms show results for the data-generating SSRT distribution shown in the first panel in the second row of Fig. 1. The gray triangles indicate the data-generating true values; these correspond thus to the median of the black histograms. The percentages show the coverage of the central 95% CIs

These results also illustrate that if a researcher were to fit the SS-LNR to empirical data generated from a true SSRT distribution with plausible levels of variability, and then used the resulting parameter estimates to assess the recovery performance of the model, they would mistakenly conclude that estimation is adequate. In reality, however, successful recovery is purely a consequence of using a specific set of data-generating parameter values, the biased estimates that correspond to a SSRT distribution with near-zero variance and extremely steep leading edge. In the discussion, we revisit the implications of this phenomenon of misleading parameter recovery.

Stop-Signal Racing Wald Model

We now present the results of two sets of parameter-recovery studies for the SS-RW. Both sets used a standard two-choice stop-signal design featuring only a stimulus factor (e.g., right or left arrow). The first set assumed the following five go parameters: v_T and v_F for the rate of evidence accumulation that matches and mis-matches the stimulus, respectively, B, A, and non-decision time t_g. For the stop accumulator, we assumed v_Stop, B_Stop, A_Stop, and C. Figure 4 shows the true data-generating go RT and SSRT distributions, and Fig. 5 shows the true values. In the second set, we used the same setup with the exception that A_Stop was fixed to 0, with the true SSRT distribution strongly resembling the one shown in Fig. 4. We investigated this setting because estimation of start-point variability is notoriously difficult (Boehm et al. 2018; Castro et al. 2019), and so fixing it to zero might improve estimation performance for the remaining parameters. We again examined four sample sizes, but for the sake of brevity we only discuss the 200 and 3200 stop-trial scenarios because (1) recovery of the stop parameters was poor even in the near-asymptotic case; and (2) the results for the 100, 200, and 400 stop-trial scenarios were virtually indistinguishable.

Fig. 4

True and predicted RT distributions for the SS-RW. For the go RT distribution, the black density line corresponds to correct RTs and the red density line corresponds to error RTs

Fig. 5

Parameter recovery for the SS-RW with and without A_stop as a function of the number of go and stop-signal trials. The horizontal dotted lines indicate the true values. The black bullets show the median of the posterior means across the 200 replications. The error bars show the median width of the central 95% CIs across the replications. The percentages indicate the coverage of the CIs. The ranges of the y-axes correspond to the ranges of the uniform prior distributions on the model parameters

Full SS-RW with A_Stop

Figure 5 shows parameter-recovery results for the full SS-RW with A_Stop as a function of the number of go and stop-signal trials. The Supplemental Materials show detailed results, including the distribution of the posterior means and representative posterior distributions (Figure S8). The Appendix in the Supplemental Materials provides examples of the MCMC chains.

The recovery of the go parameters is excellent: the estimates closely approximate the true values, and the coverage of the 95% CIs is close to nominal. As expected, the uncertainty of the estimates decreases as the number of go trials increases. In contrast to the go estimates, the stop estimates are heavily biased regardless of the sample size. In the near-asymptotic case with 3200 trials, v_Stop is underestimated, whereas A_Stop is slightly overestimated. The situation is more worrisome for C and B_Stop. C is severely overestimated, whereas B_Stop is severely underestimated; B_Stop is in fact estimated near zero for more than 90% of the replications. The 95% CIs are very narrow, and their coverage is far from nominal: the CIs of B_Stop, A_Stop, and C contain the true values in only 5–6% of the replications. With 200 stop-signal trials, v_Stop, B_Stop, and A_Stop are strongly overestimated, whereas C is underestimated. Note, however, that for the majority of the replications, the uniform prior distributions of v_Stop and A_Stop are barely updated and the posteriors are truncated by the upper bound of the priors (see Figure S8). This problem persisted even after quadrupling the prior range, indicating the data simply do not provide sufficient information to constrain the posteriors.⁴ Additionally, the distributions of the posterior means of v_Stop, B_Stop, and A_Stop are bimodal. This suggests that the MCMC chains got stuck on two different ranges of values of the simulated distribution, which can be thought of as a kind of local minimum problem. Note that bimodality in the posterior means was not reflected in bimodality in the posterior distributions themselves. In fact, the more prominent mode of the distribution of the posterior means was far away from the average start values and was typically more than an order of magnitude higher than the data-generating values. These results suggest that the reported biases are unlikely to reflect sampling problems associated with the presence of local minima. The Supplemental Materials show similar performance for fixed SSDs, high-accuracy paradigms, informative prior distributions, and a more complex design that features the manipulation of the stop parameters (Figures S9–S11).

The third panel of Fig. 4 shows the predicted SSRT distribution that was generated using the median of the posterior means of the stop estimates from the simulations with 3200 stop-signal trials. We did not explore the 200 stop-trial scenario because of the artificially truncated posterior distributions. Similar to the SS-LNR, the stop estimates are jointly pulled toward a parameter region where the predicted SSRT distribution has near-zero variance and an unrealistically steep leading edge, with C—and consequently the mode—approximating the mode of the true SSRT distribution, although not as closely as for the SS-LNR (estimated C = 0.199, estimated mode =0.200, and true mode =0.236). In contrast to the SS-LNR, however, this pathological behavior is present not only in small samples but also in the near-asymptotic case. These results reinforce our earlier conclusion about a trade-off between SSRT variance and the lower bound C.

The identification problem resulting from this trade-off and the associated danger of misleading parameter recovery is illustrated in Fig. 6 where we compare recovery performance for a SSRT distribution with appreciable variance and one with near-zero variance. The black density lines (right panels) and histograms (left panels) show the 200 posterior distributions and the distribution of the corresponding 200 posterior means, respectively, for the recovery study with 3200⁵ stop-signal trials using the distribution shown in the middle panel of Fig. 4 as the data generating SSRT distribution. Note that the same results are also summarized in Fig. 5. The black triangles show the true values and the gray triangles show the median of the—heavily biased—posterior means across the 200 replications. The gray density lines and histograms show the results of a new recovery study where we used a distribution with near-zero variance shown in the right panel of Fig. 4 as the data-generating SSRT distribution. In the new simulation, the true values equal the biased estimates from the first recovery study depicted by the gray triangles. As shown in Fig. 6, parameter recovery in the new parameter region is substantially better, in terms of both bias and coverage. Just as for the SS-LNR, these results illustrate that it can be misleading to rely on parameter-recovery studies that use biased SS-RW estimates as data-generating values.

Fig. 6

Misleading parameter recovery for the SS-RW. The black density lines and histograms show the 200 posterior distributions and the distribution of the corresponding 200 posterior means, respectively, from the recovery study with 3200 stop-signal trials generated by the SSRT distribution in the middle panel of Fig. 4. The black triangles show the true values, and the gray triangles show the median of the posterior means across the 200 replications. The gray density lines and histograms show results for the data-generating SSRT distribution shown in the right panel of Fig. 4. The gray triangles indicate the true values; these correspond thus to the median of the black histograms. The percentages in the right panels show the coverage of the central 95% CIs. The percentages in the left panels show the proportion of replications that resulted in extreme estimates and were excluded from the figures to increase visibility

SS-RW Without A_Stop

Figure 5 shows parameter-recovery results for the SS-RW without A_Stop (indicated as “-AS”) as a function of the number of go and stop-signal trials. As expected, the recovery of the go parameters is excellent. The bias in the stop estimates decreases substantially relative to the model with A_Stop, but the coverage of the 95% CIs is still unsatisfactory. As shown in the Supplemental Materials, the distributions of the posterior means are bimodal, with a minority of the estimates relatively close to the true values, but the majority showing—depending on the parameter—an upward or downward bias (Figure S14). The lower bound C is typically underestimated even in the near-asymptotic case; in fact with 3200 stop trials, the majority of the C estimates approaches zero.

In the Supplemental Materials, we show that poor parameter recovery is not unique to the particular setup used in our simulations and is not necessarily improved by imposing highly informative prior distributions (Figures S15–S17). We did not explore the possibility of misleading parameter recovery using the biased estimates as true values because zero or near-zero estimates of lower bounds in RT distributions would not be considered as reasonable data-generating values in most applications.

Fitting Empirical Data

We next investigated the behavior of the SS-LNR and SS-RW in fits to empirical stop-signal data reported by Matzke et al. (2019). The two-choice go task required participants to indicate with a button press whether a random-dot kinematogram displayed 45° left or right upward global motion. The difficulty of the go task was manipulated on two levels (Easy vs. Difficult) by varying the percentage of dots moving in a uniform direction, with higher coherence supporting easier perceptual judgments. Participants were instructed to withhold their response to the go stimulus when the stop signal (i.e., a gray square boarder around the go stimulus) was presented. As previously mentioned, the experiment used 395 go and 144 stop-signal trials, which is intermediate between the two lowest sample sizes used in our parameter-recovery studies. SSD was set using the staircase-tracking algorithm with step size of 0.033s.⁶

We report the results of fits to the data of a single participant, with an average error rate of 31%. We chose this particular participant because both the SS-LNR and SS-RW models resulted in interpretable parameter estimates in the sense that the posterior distributions converged to the stationary distribution ($\hat{R}<1.1$) and were not truncated by the prior bounds. The data from the other participants are available in the Supplemental Materials of Matzke et al. (2019) at https://osf.io/me26u/. To investigate the possibility that the results may reflect local minima, as was sometimes the case in the recovery studies, we repeated the analyses six times. The problem of local minima was exacerbated in real data: In contrast to the simulations, it also affected the SS-LNR and often influenced the go estimates in both models. Here we present estimates corresponding to the solution with the highest (posterior) log-likelihood.

Stop-Signal Lognormal Race Model

We used a 13-parameter SS-LNR, where the go parameters μ_T, μ_F, σ_T, σ_F, and t_g were free to vary with task difficulty, whereas the stop parameters μ_Stop, σ_Stop, and C were constrained between the Easy and Difficult conditions. We chose for a flexible parameterization to ensure that the stop parameters are not (unduly) influenced by constraints on the go parameters.

Figure 7 shows the posterior distribution of the stop parameters. The posteriors of the go parameters are available in the Supplemental Materials (Figure S19). The posteriors of μ_Stop and σ_Stop are quite wide, indicating a large degree of uncertainty in estimating these parameters. The posterior of C is bimodal and the estimate is relatively high. The right panel shows the predicted SSRT distribution that was generated using the mean of the posterior distribution of the stop estimates. Similar to the parameter-recovery results, the predicted SSRT distribution has near-zero variance and an unrealistically steep leading edge.

Fig. 7

Prior (red lines) and posterior distributions estimated from empirical data with the SS-LNR. The right panel shows the predicted SSRT distribution generated by the mean of the posterior distributions

We used posterior predictive simulations (Brooks and Gelman 1998; Gelman and Rubin 1992) to assess the descriptive accuracy of the model; the results are presented in the Supplemental Materials (Figures S20–S21). Despite the severely biased estimates, the SS-LNR provided an adequate characterization of the CDF of go RTs and signal-respond RTs, and captured the increase in response rate and median signal-respond RTs as a function of increasing SSD. Assessing the descriptive accuracy of the model is thus insufficient to detect the bias in the parameter estimates, likely because the mode of the SSRT distribution is captured relatively well by the SS-LNR.

Stop-Signal Racing Wald Model

We fit both versions of the SS-RW using a flexible parameterization. The full model featured 13 parameters, where the go parameters v_T, v_F, B, and t_g were free to vary with task difficulty, whereas A for the go accumulator and the stop parameters v_Stop, B_Stop, A_Stop, and C were constrained between the Easy and Difficult conditions. The restricted version used the same parameterization with the exception that A_Stop was fixed to zero.

Figure 8 shows the posterior distribution of the stop parameters. The posteriors of the go parameters are available in the Supplemental Materials (Figures S22–S23). The posteriors are relatively well-constrained, and the two sets of estimates are quite similar. Note, however, that the estimated C parameter is again relatively high. C was in fact estimated to be higher than the non-decision time of the go process t_g, an unlikely result given that the go and stop stimuli were presented in the same modality and—unlike the go process—the stop process does not produce an overt response. The right panels in Fig. 8 show the predicted SSRT distributions that were generated using the mean of the posterior distribution of the stop estimates. Similar to the simulations, the SSRT distribution predicted by the full SS-RW has low variance and a very steep leading edge. Unlike in the simulations where C was pulled to zero, the SSRT distribution predicted by the SS-RW without A_Stop follows the same pattern in this parameter region.

Fig. 8

Prior (red lines) and posterior distributions estimated from empirical data with the full SS-RW (top panel) and the SS-RW without A_Stop (bottom panel). The right panels show the predicted SSRT distributions generated by the mean of the posterior distributions

The results of the posterior predictive simulations are presented in the Supplemental Materials (Figures S24–S27). Both SS-RW models provided an adequate characterization of the CDF of go RTs and signal-respond RTs, and captured the increase in response rate and median signal-respond RTs as a function of increasing SSD. Again, assessing the descriptive accuracy of the model is thus insufficient to detect the bias in the parameter estimates.

Discussion

Our goal was to examine whether stop-signal evidence-accumulation models can serve as measurement models that can be used to quantify the psychological processes represented by the model parameters. We investigated two instantiation on the stop-signal evidence-accumulation framework: the stop-signal lognormal race (SS-LNR) and the stop-signal racing Wald (SS-RW) models. Our parameter-recovery studies indicated that neither the SS-LNR nor the SS-RW is suited as measurement models in standard applications of the stop-signal paradigm with a realistic number of trials. The results can be summarized as follows.

For the SS-LNR, where the finishing-time distribution of the evidence accumulators is lognormal, recovery of the parameters corresponding to the go runners was excellent even for the smallest sample size (i.e., 300 go and 100 stop-signal trials). In contrast, recovery of the parameters corresponding to the stop runner was poor, unless a very large number of trials was available. For realistic sample sizes, the stop parameters were heavily biased, resulting in severe underestimation of the variance and overestimation of the lower bound of the SSRT distribution. For the near-asymptotic case of 9600 go and 3200 stop-signal trials, the estimates were, on average, relatively accurate, but estimates of the lower-bound C were variable and the posterior distributions were poorly calibrated.

For the SS-RW, where the finishing times of the evidence accumulators follow a Wald distribution, recovery of the go parameters was good even for small sample sizes, although as expected not as good as for the SS-LNR. The recovery of the stop parameters was substantially worse than for the SS-LNR, with C severely overestimated and the decision threshold B severely underestimated even for the near-asymptotic case. As for the SS-LNR, this particular pattern of bias resulted in underestimation of the variance and overestimation of the lower bound of the SSRT distribution. From a practical standpoint, working with both models was difficult because of the problem of multiple distinct but almost equally good fits.

For both models, we observed a trade-off between the estimated variance and the lower-bound C of the finishing-time distribution of the stop runner (i.e., the SSRT distribution). This pattern acted as an “attractor,” distorting all estimates corresponding to the stop runner. Given that SSRT variance can be estimated accurately with parametric methods in models that do not assume a parameter-dependent lower bound (e.g., BEESTS; Matzke et al. 2013), our results indicate that the recovery problems arise from difficulties with estimating C, at least in realistic sample sizes. Indeed, we show in the Supplemental Materials that when C is fixed to its true value, recovery of the SS-LNR stop parameters is excellent, even with only 100 stop-signal trials (Figures S6–S7). Note, however, that using a very restrictive prior distribution with a 100-ms range on C did not have the same beneficial effect (Figures S3 and S5). For the SS-RW, fixing C to its true value substantially improved estimation for the near-asymptotic case, but not for smaller sample sizes (Figures S12–S13); small samples did not seem to provide sufficient information to estimate the remaining stop parameters v_Stop, B_Stop, and A_Stop. This is perhaps not surprising as it can be difficult to separately estimate thresholds and rates for a single-boundary diffusion process even when finishing times are observable (see parameter recovery in Castro et al. 2019).

The trade-off between SSRT variance and lower bound C signals an identifiability problem, where data-generating SSRT distributions with similar central tendency (mode) but different variances and lower bounds can yield very similar parameter estimates and the corresponding characteristically peaked “J-shaped” predicted SSRT distribution. That is, the J-shaped distribution forms an attractor, with many different true data-generating values producing the same parameter estimates. As we illustrated in Figs. 3 and 6, this behavior can result in successful but spurious parameter recovery. In particular, if a researcher were to fit the SS-LNR or SS-RW to empirical data generated from a true SSRT distribution with plausible levels of variability, and then used the resulting—biased—estimates to assess the performance of the model, they would conclude that parameter recovery was successful. However, this conclusion is mistaken as successful recovery is purely a result of using a specific set of data-generating parameter values that correspond to a J-shaped SSRT distribution. The attractor behavior is dangerous, because it could mislead even cautious researchers who follow recommended practices and perform parameter-recovery studies for their particular experimental design (Heathcote et al. 2015a), at least when the recovery is based on data-generating values obtained from fits to empirical data.

In the hope to constrain the SS-RW, we also examined a simpler version of the model where we fixed start-point variability A to zero. However, this has not improved recovery performance; the distribution of the estimates became bimodal, with a minority of the estimates close to the true values but a majority still severely biased. The pathology for C was now different from the full model, with values now being underestimated. This underestimation was so severe, with most estimates near zero, that at least if researchers obtained such results they would likely assume them to be spurious and so would not be misled. In the small-sample scenario, the bimodality in the posterior means was occasionally accompanied by bimodal posterior distributions, with modes approximating the two modes of the distribution of the posterior means. Although this particular pattern may reflect sampling problems, we believe that even these results are highly informative for researchers working with these models: Despite the possibility of sampling problems resulting from local minima, the vast majority of fits—even for the small-sample scenarios—resulted in seemingly converged and well-behaved unimodal posteriors. In real-world applications, where we do not know the true data-generating values, this behavior is clearly problematic and may lead to biased inference. As shown in the Supplemental Materials, fixing C to its true value substantially improved estimation, especially for the near-asymptotic case; in small samples, the distribution of the posterior means as well as the posterior distributions themselves still exhibited some bimodality, at least in the parameter region we had examined (Figures S12 and S18).

The problems we identified in the parameter-recovery studies were also evident in fits to real data from Matzke et al. (2019). Despite this, the models provided an adequate characterization of the CDF of go RTs and signal-respond RTs, and captured the increase in response rate and median signal-respond RT as a function of increasing SSD, likely because the mode of the SSRT distribution was captured relatively well by all models. Hence, goodness-of-fit for observable performance provides no guidance as to whether parameter identifiability problems are present. Both the SS-LNR and the SS-RW had severe problems with local minima, producing many inconsistent solutions with almost equally good fits, the pattern that initially lead Matzke et al. not to use the SS-RW with these data. The only difference from the parameter-recovery results was that the SS-RW with A_Stop = 0 produced a large rather than small estimate of C. The large estimate might be viewed as implausible because C was much slower than the non-decision time of the go runner t_g, even though stop and go stimuli were presented in the same modality. Note that Logan et al. (2014) also reported a similar pattern, where the non-decision time of the go process was estimated at 0.164 and 0.160 in the aggregate and the individual fits, respectively, whereas the non-decision time of the stop process was estimated at 0.241 in both cases. Logan et al.’s stop signal was auditory and the go stimulus visual, and it is usually assumed that transduction for auditory stimulation is, if anything, faster than for visual stimulation. Although it is impossible to categorically reject Logan et al.’s parameter estimates on these grounds, the fact that the estimates showed the same pattern that we found in our simulations, with predicted SSRT distributions having very little variance, suggests that they were distorted by the attractor behavior identified in this paper.

However, it is important to note that Logan et al. (2014) did not rely on the stop estimates to make psychological inferences. Their conclusion that the stop and go processes do not share capacity, and that there is a change in the capacity required by the go process with the number of choice alternatives, was based on model selection using the BIC. The BIC relies on goodness-of-fit and a count of the number of parameters in the models, where the latter is used as a complexity penalty. It is only in cases with multiple local minima that estimates of goodness-of-fit may be compromised, which is unlikely given the large number of trials used by Logan et al. They did rely on the sum of the go rate estimates over accumulators to infer that capacity is limited, but our results indicate adequate recovery for the go parameters for Logan et al.’s sample size.

Although these considerations suggest that Logan et al.’s (2014) psychological inferences are on solid ground, we urge caution in any further applications of parameter inference and model selection for the SS-RW, particularly in designs with a relatively small number of trials. In particular, future work should assess the performance of various model-selection methods (e.g., Evans et al. 2020) to evaluate whether and under what circumstances they provide valid and useful tools for psychological inference in stop-signal evidence-accumulation models. But for now, the only point on which our results clearly contradict Logan et al. is their claim that the SS-RW provides valid estimates of the distribution of SSRTs: our findings indicate that the SS-RW can severely underestimate SSRT variability and overestimate its lower bound.

It might be tempting to conclude from our results that the SS-LNR might provide a viable measurement model in designs with a very large number of stop-signal trials. However, we urge caution based on the likely occurrence of non-negligible levels of trigger failures in real data, which can substantially bias the stop estimates (Matzke et al. 2017a; Skipppen et al. 2019; Weigard et al. 2019). Matzke et al. (2017b) found that although the addition of trigger failures to the ex-Gaussian stop-signal race model made estimation more difficult, it remained viable even in relatively small samples. In simulations not reported here, we also investigated the effects of adding trigger failures in the SS-LNR and SS-RW. For the SS-LNR, the degradation was more marked than for the ex-Gaussian race model, indicating that the SS-LNR is unlikely to be useful in practice, even with a very large number of trials. For the SS-RW, the situation was even more troubling; we were not able to obtain converged estimates when including the additional trigger failure parameter in the model, not even for the near-asymptotic case.

We are more optimistic about measurement applications of the SS-LNR in situations where it is possible to obtain an independent estimate of the lower-bound C of the SSRT distribution. Indeed, when C was fixed to its true value, the SS-LNR provided accurate and well-constrained parameter estimates with as few as 100 stop-signal trials, which is similar to, and maybe even better than, the performance of the ex-Gaussian race model when implemented in a non-hierarchical setting. We note, however, that preliminary simulations indicate that independent estimates of the lower bound of the stop runner will have to be quite precise to be useful. Fixed lower bounds have been used for modeling the anti-saccade task, which is closely related to the stop-signal task, except that choice is not required for the go component. Hanes and Carpenter (1999) assumed a lower bound (an “irreducible minimum processing time”) of 60 ms for the visual go and stop stimuli based on the onset latency of visual cells in the macaque visuomotor system (see also Ramakrishnan et al. 2010; Walton and Gandhi 2006). Colonius et al. (2001) assumed the same lower bound for a visual go stimulus and a shorter—20 ms—lower bound for an auditory stop signal. We are concerned that the use of such fixed values requires the strong assumption of no individual differences, and that the appropriate value might vary with the nature of the stop signal. Another potential avenue might be to directly obtain constraints on the lower bound from brain activity recorded simultaneously with stop-signal performance using the model-based neuroscience approach (e.g., Forstmann and Wagenmakers 2015).

Our investigations relied exclusively on Bayesian methods using DE-MCMC sampling. However, we feel that this is anything but problematic, as Miletic et al. (2017) found that Bayesian methods were superior to maximum-likelihood estimation in the context of the Leaky Competing Accumulator model (LCA; Usher and McClelland 2001), which is also plagued by identifiability problems. Although it is possible that alternative MCMC samplers may perform better in the context of stop-signal evidence-accumulation models, this is unlikely because our earlier implementation of the SS-LNR in the WinBUGS Developmental Interface (Lunn 2003), which relies on a different sampler, was also unsuccessful. Further, Logan et al. (2014) incidentally reported parameter-recovery results based on maximum-likelihood methods in a simulation study aimed at showing that the SS-RW could produce fast error responses. Despite the large number of trials, recovery of the stop parameters was not ideal, with a nearly 30-ms overestimation of the lower-bound C.⁷ Note also that the predicted SSRT distribution generated using the maximum-likelihood estimates of the SS-RW stop parameters reported by Logan et al. closely resembles the characteristic peaked shape identified by our investigation (see Supplemental Figure S28). An alternative avenue would be to pursue quantile-based optimization methods, which—unlike likelihood-based methods—are robust to the problems caused by irregularity (Heathcote and Brown 2004). However, it remains to be shown if this will be helpful in the present context where the SSRT distribution cannot be directly observed. Note also that the quantile-based approach would necessarily forgo the many advantages of Bayesian inference. In general, future research should examine whether parameter-recovery performance depends on the interaction between the properties of stop-signal evidence-accumulation models and the particular estimation procedure used.

Another potential limitation is that the SS-LNR and SS-RW may be better behaved in parameter settings or designs that we did not investigate here, although, as reported in the Supplemental Materials, we did canvas a number of different possibilities, including a comparison of parameter recovery for the SS-LNR in three different parameter settings (Supplemental Figure S29). These results show an identical pattern of bias as reported for the parameter setting we examined in the main text. Although the additional simulations are not comprehensive (cf. White et al. 2018), they suggest that the SS-LNR does not only fail to recover the absolute value of the stop parameters but also fails to maintain the ordering of the parameters and is unable to unambiguously differentiate between the estimates even in the presence of large differences between data-generating values.

We also acknowledge that various other instantiations of the evidence-accumulation framework are possible. For example, Logan et al. (2014) also explored stop-signal evidence-accumulation models based on the Poisson counter (Van Zandt et al. 2000) and the linear ballistic accumulator (LBA; Brown and Heathcote 2008) models, but did not pursue them because they did not fit as well as the SS-RW. However, given that these models are similarly complex as the SS-RW, it seems unlikely that they would perform substantially better. The same pessimism applies to more complex models such as the interactive race model (Boucher et al. 2007) and blocked input models (Logan et al. 2015), although because these models directly address the implementation of stopping in the brain, they are in a better position to take advantage of constraints from neural data. One possible avenue to explore is the Linear Approach to Threshold with Ergodic Rate (LATER; Carpenter 1981; Carpenter and Williams 1995), a simplification of the LBA which has been used to model stopping performance in the anti-saccade task. However, LATER also assumes a lower bound for the finishing times and therefore seems unlikely to perform substantially better than the SS-LNR. Note also that most, if not all, stopping applications of LATER, have forgone the estimation of the lower bound of the runners and fixed it to a constant (e.g., Colonius et al. 2001; Hanes and Carpenter 1999; Ramakrishnan et al. 2010; Walton and Gandhi 2006).

Given that our findings specifically implicated the lower bound of the stop runner as the cause of identifiability problems, perhaps the most immediately promising avenue to obtain a measurement model requires dropping this assumption. Matzke et al.’s (2019) stop-signal race model using the ex-Gaussian distribution to model the go and stop processes does so with excellent measurement properties, and with the ability to account for failures to trigger the stop and the go runners. A lesser change would be to retain the evidence-accumulation framework for the go processes, so that some of the advantages of this approach could be maintained (see White et al. 2014, for a related approach). For example, such a model could answer Logan et al.’s (2014) question about go capacity limitations. We have obtained promising preliminary results for this “hybrid” approach, where we use the ex-Gaussian distribution to model the finishing times of the stop runner while retaining the Wald assumption for the go runners. However, this approach would be unable to clearly answer Logan et al.’s question about stop capacity, which could be confounded by a trade-off between rate and threshold changes, and obviously could not address Matzke et al.’s (2017a) question about lower bounds.

In any case, given our results, we urge the adoption of thorough case-by-case parameter-recovery studies for any alternative proposal that seeks to develop a measurement model of the stop-signal paradigm. We also recommend that such studies address the possibility that parameter estimates may reflect the presence of an attractor region. Indeed, we believe that an important broader implication of our investigation is that parameter-recovery studies should investigate data-generating values that deviate from estimated parameters so that researchers do not gain a false sense of security from possibly misleading recovery results.

Conclusion

The goal of this article was to investigate whether stop-signal evidence-accumulation models can serve as measurement models that can be used to quantify psychological processes in terms of estimated parameter values. We found that this was not the case. In realistic experimental designs, both models we examined—the stop-signal lognormal race and the stop-signal racing Wald—produced biased and variable parameter estimates. However, we acknowledge that cognitive models do not necessarily need to be measurement models to be useful. Models with suboptimal measurement properties can still provide insights into cognitive architectures by virtue of the selective influence of experimental manipulations on the model parameters and by enabling the comparison of different formalizations of performance in a given experimental paradigm (e.g., Evans et al. 2020). Future research should investigate whether and under what circumstances stop-signal evidence-accumulation models provide useful tools for psychological inference, despite their undesirable measurement properties.