Links between electrochemical thermodynamics and kinetics

Abstract

Redox systems are considered when proceeding (a) in an electrochemical cell (heterogeneous reactions), and (b) in a single compartment (homogeneous reactions), also including the case of a solution in contact with solid phases. Special emphasis is given to the electrochemical systems. Starting from equilibrium states in the individual half-cells, the cell as a whole is (1) made to work spontaneously (batteries, fuel cells) and (2) forced to induce non-spontaneous transformations (electrolysis). Kinetics needs to be considered in both cases: phenomenological aspects and rigorous mathematic tools are intended to concur to draw the picture. Supplementary material is given in order to help visualise what the equations given express.

Introduction

This contribution supplements the paper that has appeared in this journal on the thermodynamic aspects of electrochemical cells [1]. In the present article, the attention is focused on the inherent link between the thermodynamics and kinetics of electrochemical systems. Treating the kinetics, reference should always be made to thermodynamics, i.e. to static systems or to systems that only evolve in ideal conditions. This means that some concepts and equations already present in [1] will be also reported here.

Electrochemistry possesses a most powerful tool to shift equilibria (thermodynamics), and to change reaction rates (kinetics): this is the electrode potential. This tool allows one to significantly change the free energy content of reactants, products, and even transition state, by imposing an electric field: as a consequence of the so-called inner potential (ϕ)¹ of the phase, the electrically charged species in solution acquire an electrical energy (G _e). The electrical energy is a component of the electrochemical Gibbs free energy ($\tilde{G}$) of a charged species; it has to be added to the chemical Gibbs free energy (G _c) in order to fully account for the overall energy content of charged species [2]. In electrode processes, the energetics of an oxidation or of a reduction reaction can be changed dramatically. By considering a conductor (assumed to be a metal, for the sake of simplicity) dipped in the (solution) phase where the electroactive species are present, an electrical potential difference is build up between the metal phase (M) and the solution phase (s): the Galvani potential difference (Δϕ ^M,s) conditions the overall free energy content of the redox system, through a corresponding electrical free energy difference. The chemical component (being compound and solvent specific) depends only on temperature and pressure, changes of which are much less effective in driving properly the charge transfer between the metal and the electroactive species in solution. Charge transfer implies electron transfer or ion transfer (e.g. in the case of metal deposition or dissolution); electron transfer will be considered in the following. Electron transfer takes place until the electrochemical free energies of reactants and products are equal to each other. Similar to the denomination of chemical potential (μ) ascribed to the molar chemical free energy, the term electrochemical potential ($\tilde{\mu }$) is given to the molar electrochemical free energy. The general expression for a chemical equilibrium expresses the equal content of energy between the stoichiometric quantities of reagents and products, so that the driving forces for a chemical net reaction are zero:

$$\mathop \sum \limits_{i} \nu_{i} \tilde{\mu }_{i} = 0$$

(1)

where $\nu_{i}$ are the stoichiometric coefficients of the reaction species and the electrochemical potential is defined by:

$$\tilde{\mu }_{i} = \left( {\frac{{\partial \tilde{G}}}{{\partial n_{{{\text{mol}},i}} }}} \right)_{T,p,j \ne i} = \mu_{i} + z_{i} F\phi^{\alpha }$$

(2)

In turn:

$$\mu_{i} = \left( {\frac{{\partial G_{\text{c}} }}{{\partial n_{{{\text{mol}},i}} }}} \right)_{T,p,j \ne i}$$

(3)

z _i is the charge of the species, ϕ ^α is the inner potential felt by species i in the α phase, and $\tilde{G}$, the electrochemical free energy, is the sum of a chemical and an electrical contribution:

$$\tilde{G} = G_{\text{c}} + G_{\text{e}}$$

(4)

Equation (3) defines the chemical potential of the ith species as the infinitesimal variation in G _c associated with an infinitesimal variation in the number of mols of the ith component, n _mol,i , at temperature (T, absolute or thermodynamic temperature), pressure (p) and contents of the other j − 1 components kept constant. It is ascribed to the purely chemical properties of the ith species, not including the energy depending on the electric charge, to take into account in the case of electrically charged species, as expressed by Eq. (2). Equation (1) may be also expressed as $\mathop \sum \limits_{i} \nu_{i} \mu_{i} = 0$, being $\mathop \sum \limits_{i} z_{i} F\phi^{\alpha } = 0$.

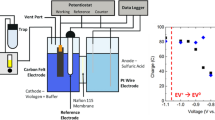
The fact that the half-cell,² consisting of the metal (electrode) (see footnote 2) and of the solution in contact with it, is necessarily complemented by a second half-cell will be considered in the following, because it is meaningless in respect of what is intended here. A galvanic cell is represented in one of the possible configurations of the electrochemical system drawn in Fig. 1.

Fig. 1

Electrochemical system suitable to represent different situations. Depending on the configuration with respect to switch S, on the value imposed to the variable resistance R _v and to voltage from an outer source, ΔV, the different situations depicted in the text are realised. Galvanic cell: S switch open, R _v assuming finite values; potentiometric cell: S switch open, R _v  → ∞; electrolytic cell: S switch closed, R _v  → ∞, ΔV working as a voltage generator

With reference to the scheme in Fig. 1, equilibrium can be achieved by turning off the switch S and by adjusting R _v so that a reasonable current can flow: the current flows because a spontaneous reaction is possible, and as a result, the Galvani potential difference in both half-cells lowers. On the other hand, insertion of an active electrical element, namely a voltage source, is also possible: it increases the Galvani potential difference in both half-cells, reversing the direction of a process with respect to the spontaneous one. In the latter case, the cell system drifts away from the equilibrium conditions more and more.

In all cases, when an electrochemical reaction proceeds, its kinetics is as important as its thermodynamics. The strong interplay between thermodynamics and kinetics constitutes the background to all what is dealt with here.

We decided to start dealing with a spontaneous redox reaction occurring in a galvanic cell, although the reaction can also proceed in a single compartment (e.g. in a homogeneous solution, or a solution system with solid phases). We like to discuss here electrochemical cells, because they allow the control of the process, in principle even to let it proceed reversibly, i.e. under thermodynamic conditions. In particular, Refs. [1, 2] will be the bases of the discussion throughout the whole article. Refs. [3–14] will be of invaluable importance to complement what is discussed here.

Thermodynamics of ideally reversible processes

The Gibbs free energy, G, is a state function: ΔG for the transition of a system from A to B states it does not depend on the path followed; it does not depend on the rate of approaching the equilibrium either.

The following relationship holds:

$$\Delta G = q - w_{\text{u}}$$

(5)

where q is the heat exchanged with the environment (<0 when released) and w _u is the so-called useful work made by (>0) or on (<0) the system. The term ‘useful work’ indicates that it does not include the work due to volume expansion or contraction.

The galvanic cell in Fig. 1 is particularly effective in illustrating the transition from a reversible to a non-reversible process, with reference to Eq. (5). The aim of a galvanic cell is to convert the free energy content of spontaneous reaction into a form of work that can be profitably used, be it electric or mechanical work, or whatever other form of useful work. In principle, also the extent of energy converted to heat may be in turn converted into work; however, this is a disadvantageous path, since the conversion factor of q to w _u is <1. In a real process, i.e. in a non-reversible process, the energy loss due to released heat can only be minimised, not zeroed. In other words, only in a process carried out reversibly q = 0, so that:

$$w_{\text{u}} = - \Delta \tilde{G} = w_{{u,{ \hbox{max} }}}$$

(6)

w _u,max representing the maximum useful work achievable. In any real situation encountered,

$$w_{{u}} < - \Delta \tilde{G}$$

(7)

Let us consider the following redox cell reaction occurring in the galvanic cell³ in Fig. 1:

$$a\,{\text{Ox}}_{1} + b\,{\text{Red}}_{2} \, \leftrightarrows \,a\,{\text{Red}}_{1} + b\,{\text{Ox}}_{2}$$

(8)

For the sake of simplicity, the electric charges carried by Ox₁ and Ox₂, by Red₂ and Red₁, as well as by Ox and Red in the following, i.e. z _Ox and z _Red, respectively, are not indicated. It is the cell reaction; n electrons are stoichiometrically involved. If R _v  → ∞, the process occurs reversibly and

$$- \Delta \tilde{G} = nFE_{\text{cell}}$$

(9)

where

$$E_{\text{cell}} = E_{\text{cell}}^{\emptyset } + \frac{RT}{nF} { \ln }\frac{{a_{{{\text{Ox}}_{2} }}^{b} a_{{{\text{Red}}_{1} }}^{a} }}{{ a_{{{\text{Red}}_{2} }}^{b} a_{{{\text{Ox}}_{1} }}^{a} }}$$

(10)

E _cell is the cell potential (or cell voltage), the so-called electromotive force (emf) of the cell, i.e. the potential difference, measured at zero current between the two half-cells under equilibrium conditions; $E_{\text{cell}}^{\emptyset }$ is the relevant standard cell potential, R is the gas constant, and F is the Faraday constant (96,485 C mol⁻¹), expressing the charge of 1 mol of electrons.

A closer look at the meaning of E _cell is worth; to this aim, the reaction in Eq. (8) should be further considered. In the same configuration of the cell in Fig. 1, two half-cells, labelled by numbers 1 and 2, respectively, concur to build up the whole cell. In the half-cells, the Ox₁/Red₁ and the Ox₂/Red₂ redox couples are present, respectively. The cell reaction in Eq. (8) can be formally split into two half-reactions. Each one of these cannot take place without the other:

$$a\,{\text{Ox}}_{1} + ne\, \leftrightarrows \,a\,{\text{Red}}_{1}$$

(11)

$$b\,{\text{Red}}_{2} \, \leftrightarrows \,b\,{\text{Ox}}_{2} + ne$$

(12)

Though not individually measurable, two half-cell potentials may be correspondingly written; each half-cell is individually under equilibrium conditions:

$$E_{{{\text{eq}},1}} = E_{1}^{\emptyset } + \frac{RT}{nF} { \ln }\frac{{ a_{{{\text{Ox}}_{1} }}^{a} }}{{ a_{{{\text{Red}}_{1} }}^{a} }}$$

(13)

$$E_{{{\text{eq}},2}} = E_{2}^{\emptyset } + \frac{RT}{nF} { \ln }\frac{{a_{{{\text{Ox}}_{2} }}^{b} }}{{ a_{{{\text{Red}}_{2} }}^{b} }}$$

(14)

Half-cell potentials, as expressed by Eqs. (13) and (14), cannot be actually measured, as it always happens for the potential of a single point. Only potential differences between two points (two electrodes in our case) are measurable. This is the reason why the half-cell potentials are actually the cell potential measured for a cell in which the second half-cell is a so-called standard hydrogen electrode (SHE) [1], to which a value of 0 V is conventionally given. Keeping this well present, we can express the Nernst equation for single half-cells [Eqs. (13) and (14)]. $E_{1}^{\emptyset }$ and $E_{2}^{\emptyset }$ are the standard potentials of the relevant redox couples. It is easy to verify the obvious relationship

$$E_{\text{cell}} = E_{{{\text{eq}},2}} {-}E_{{{\text{eq}},1}}$$

(15)

and to define

$$E_{\text{cell}}^{\emptyset } = E_{{{\text{Ox}}_{1} ,{\text{Red}}_{1} }}^{\emptyset } - E_{{{\text{Ox}}_{2} , {\text{Red}}_{2} }}^{\emptyset }$$

(16)

Figure 2 summarises into a scheme what written above.

Fig. 2

The way how physical meaning is given to the individual half-cell potentials is sketched

The half-cells are physically separated from each other by the porous septum (diaphragm) shown in Fig. 1, in order to prevent mixing of reactants and products in Eq. (8). They are, however, electrically connected, thanks to the external sub-circuit (formed by the metal wires and connections) where electrons can flow, and thanks to the internal sub-circuit closed (formed by the electrolyte solution) by migration of ions through the septum, as well as inside each solution in the half-cells; the movement of ions inside the internal sub-circuit allows the system to preserve electroneutrality.

The reduction half-reaction in Eq. (11) takes place at the electrode of the half-cell 1: electrons are transferred from the electrode to the Ox₁ species in solution, charging the electrode positively. The opposite occurs in half-cell 2. The former electrode is the cathode, and the latter one is the anode; the potential difference between the positively charged electrode and the negatively charged one is a positive emf (E _cell) value. Positive E _cell implies the occurrence of a spontaneous redox reaction, as it is suggested by Eq. (9): the electrons ‘travel’ counterclockwise in the external sub-circuit, while in the internal sub-circuit anions migrate inside each half-cell and from the left to right half-cell and cations follow the opposite direction. Diffusion of the reactant species, which are present in the two half-cells, should be minimised through the septum. Otherwise, the self-discharge phenomenon would decrease the yield of transformation of chemical energy into useful work. In this respect, let’s recall that a salt bridge [1] is more effective in minimising mixing of the reactants present in the two half-cells.

Drawings of different cells, together with the relevant cell and half-cell reactions, are reported in Ref. [1]. In particular, a cell with SHE as one of the half-cells and a cell with a reference electrode (saturated calomel electrode SCE) that is actually used in the experimental frames are found there. A galvanic cell (the classical Daniell cell) is also reported.

Redox reactions in a single compartment

Before considering further the redox reactions proceeding in an electrochemical cell as depicted in Fig. 1, redox reactions in which the four reactants are in a single environment will be discussed. Oxidised and reduced species may be dissolved in the same solution (homogeneous redox reaction), or present there in solid form (heterogeneous redox reaction). The second is, for example, the case of a Zn metal bar dipped inside a solution of Cu ions [1]. The following reaction takes place: ${\text{Zn}}_{\text{M}} + {\text{Cu}}_{\text{s}}^{2 + }\, \leftrightarrows \,{\text{Zn}}_{\text{s}}^{2 + } + {\text{Cu}}_{\text{M}}$. The reaction in Eq. (8) proceeds until the redox potentials of the Ox₁/Red₁ and Ox₂/Red₂ couples become equal to each other. At the equilibrium, the final composition is the same as that in the two half-cells, considered as a whole, in the frame of a galvanic cell; however, the forward reaction takes place by ‘direct’ interaction between Ox₁ and Red₂ and the backward reaction by ‘direct’ interaction between Red₁ and Ox₂.

Homogeneous redox reactions can follow a so-called inner sphere charge transfer or an outer sphere charge transfer mechanism. Outer sphere mechanisms require that the reactants Ox₁ and Red₂ become so close to each other that the first solvation spheres are touching each other. Then, a so-called electron hopping is possible: the electron jumps from Red₂ to Ox₁ by crossing the solvation sphere closest to the reacting species. A reorganisation of the relevant solvation spheres necessarily occurs, and the energy of activation is related to solvent rearrangement energy, though not equal to it; very minor shifts take place in the geometry of Red₂ being converted to Ox₂, and of Ox₁ being converted to Red₁. In other words, energy changes ascribable to the molecules in the solvation sphere play the major role, the species changing the oxidation state retaining their own identity, and are only undergoing minor changes in the structure.

In inner sphere charge transfers, the reacting species Ox₁ and Red₂ get coupled so tightly to each other during the reaction, as to form an activated complex, which can be regarded as a ‘single’ entity. Interaction occurs between the centres involved in the electron exchange; in the case of metal complexes, for which the theory was first developed, the main energy changes connected to the electron transfer are ascribed to a variation in the bond lengths or angles between the metal and the ligands. The change in geometry poses an energy barrier to the electron transfer process as a whole. The higher the energy required for inducing the changes, the higher the activation energy, the slower the whole charge transfer. According to the crystal field theory, a change in the spin state for the metal d orbitals requires further energy, making, at the end, the transfer of the electron even slower. Furthermore, in the transition state, a ligand of two reacting complexes may be shared. An exchange of ligand(s) between the participants of the reaction may even occur, if the change in the oxidation state requires different ligand sets. Faster charge transfer occurs between molecules that possess sites through which the charge can flow, i.e. energy states close to one another. As an example, let’s consider metal complexes in which the orbitals of the metal centre contribute for the most part to Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO)⁴ of Red₂ and Ox₁, respectively. The electron exchanged needs, hence, being transferred from the HOMO of Red₂ to the LUMO of Ox₁. If the ligands contain delocalised π electron systems (e.g. phenanthroline or bipyridine, or terpyridine), the same ligands offer the electron a sort of preferential path: energy states are available to the transferring charge. It is, however, evident that it often happens that inner sphere charge transfers are not so fast as outer sphere is.

If the reaction in Eq. (8) takes place in a single compartment, it is evident that it can be only stopped from the outside by terminating the delivery of one or more of the reactants. As an example, the redox reaction cited above, involving Zn and Cu metal and relevant ions, when both metals and both salts are present in the same compartment, can only be stopped by removing the metals. On the other hand, by only extracting Cu, the reverse reaction only occurs to a minimal extent. Furthermore, no transformation into ‘useful work’ of the energy released by the reaction is possible. The energy, according to Eq. (5), is completely transformed into heat. Finally, the direction of reaction in Eq. (8) cannot be reversed.

The Marcus theory of the charge transfer, which is not dealt with here, was originally developed for outer sphere charge transfers but was subsequently extended to inner sphere redox processes, both in solution and at an electrode.⁵

Galvanic and electrolytic cells. From thermodynamic to kinetic control

More about the galvanic cell

By considering the galvanic cell in Fig. 1, the ‘useful work’ is produced by the transfer of electrical charges from one half-cell to the other, i.e. across the E _l potential difference between the two electrodes. It is evident that E _l progressively lowers when approaching the cell equilibrium in the composition of the solutions.

When the overall reaction described by Eq. (8) is realised as two separate half-cell reactions, the flow of a finite electronic and ionic current occurs in the external and internal sub-circuits of the cell, respectively: non-equilibrium states are necessarily involved in the process; to understand what kind of non-equilibrium states may be involved, we can think of the non-homogeneity of the concentrations of the species inside the solutions, where a species is consumed and another one is produced at the electrodes, creating concentration gradients different from 0 in the close proximity of the two electrodes. Then, the Joule effect,⁶ due to the flow of current, implies heating of the conductors, i.e. loss of energy in the form of heat transferred by the system to the environment. Concurrently to the non-reversibility of the cell reaction, Eq. (5) suggests to us that w _u < −Δ$\tilde{G}$. The process is no more ideally reversible and the chemical energy is not totally converted into useful work. In the experimental reality, one can increase R _v in Fig. 1 to a very high, though finite value: the current is very low, the process takes place at a very low rate, the deviation of the evolving system from equilibrium conditions is minimum, and the heat generated by the Joule effect is correspondingly low. However, the actual potential difference between the half-cells, E, is still lower than E _cell due to different ohmic drops arising in the circuit. The higher the current, the further from equilibrium the system and the higher the loss of energy due to heat release, as well as the extent of the shift of E from E _cell, of E ₁ from E _eq,1 and E ₂ from E _eq,2.

The final equilibrium, in terms of composition of the solutions, is independent of the current flowing in the galvanic cell, as well as of the occurrence of the process in an electrochemical cell (two compartments) or in a single compartment. A different path is followed, but Eqs. (1) and (5) hold, independently of how Δ$\tilde{G}$ is distributed between the terms q and w _u. The following relationship defines the equilibrium constant for reaction in Eq. (8), whatever the path through which it is reached:

$$RT\,{ \ln }\,K_{\text{eq}} = - \Delta \tilde{G}^{\emptyset } = nFE_{\text{cell}}^{\emptyset }$$

(17)

where $E_{\text{cell}}^{\emptyset }$ is given defined in Eq. (16), Δ$\tilde{G}^{\emptyset }$ is the standard change in electrochemical free energy relative to the cell reaction, also equal to $\mathop \sum \limits_{i} \nu_{i} \tilde{\mu }_{i}$, and

$$K_{\text{eq}} = \frac{{\left( {a_{{{\text{Ox}}_{2} }} } \right)_{\text{eq}}^{b} \left( {a_{{{\text{Red}}_{1} }} } \right)_{\text{eq}}^{a} }}{{\left( {a_{{{\text{Red}}_{2} }} } \right)_{\text{eq}}^{b} \left( {a_{{{\text{Ox}}_{1} }} } \right)_{\text{eq}}^{a} }}$$

(18)

Equilibrium is reached once the potentials of the half-cells, i.e. the redox couples 1 and 2, are equal to each other: the E _cell value progressively lowers, till reaching 0 at the equilibrium expressed by Eq. (18).

The free energy of a charged species changes in dependence of the inner potential of the phase: the molar free energy content of a charged species is expressed by the electrochemical potential $\tilde{\mu }_{i}$. In the α phase [see Eq. (2)],

$$\tilde{\mu }_{i}^{\alpha } = \mu_{i}^{\alpha } + z_{i} F\phi^{\alpha }$$

(19)

where $\mu_{i}^{\alpha }$ is the chemical potential of species i, possessing $z_{i}$ electrical charge, in a phase α in which it experiences an electrical inner potential $\phi^{\alpha }$.

In order to give account of the action of the electrode potential, it is necessary to consider that, at the interface of two phases, the following reaction takes place:

$${\text{Ox}}^{\text{s}} + ne^{\text{M}}\, \leftrightarrows \,{\text{Red}}^{\text{s}}$$

(20)

For the sake of simplicity, the stoichiometric coefficients of Ox and Red species are fixed to 1; M apex indicates that the electrons are in the metal and s apex indicates the solution phase in the proximity of the electrode, i.e. at a distance of closest approach, where the transfer of the electrons occurs.

The general expression for the equilibrium of a charged species between α and β phases is as follows:

$$\tilde{\mu }_{i}^{\alpha } = \tilde{\mu }_{i}^{\beta }$$

(21)

viz.:

$$\mu_{i}^{\alpha } + z_{i} F\phi^{\alpha } = \mu_{i}^{\beta } + z_{i} F\phi^{\beta }$$

(22)

At a (metal) electrode|solution interphase [Eq. (20)], the equilibrium expressed by Eq. (22) takes the form:

$$\tilde{\mu }_{\text{Ox}}^{\text{s}} + n\tilde{\mu }_{\text{e}}^{\text{M}} = \tilde{\mu }_{{\text{R} {\text{ed}}}}^{\text{S}}$$

(23)

Under equilibrium conditions, Eq. (23) may be written in the form:

$$\left( {\mu_{\text{Ox}}^{{\emptyset,{\text{s}}}} + \frac{RT}{nF}{ \ln }\,a_{\text{Ox}} + z_{\text{Ox}} F\phi^{\text{s}} } \right) + n\left( {\mu_{\text{e}}^{{\emptyset,{\text{M}}}} - F\phi^{\text{M}} } \right) = \left( {\mu_{\text{Red}}^{{{\emptyset}},{\text{s}}} + \frac{RT}{nF}{ \ln }a_{\text{Red}} + z_{\text{Red}} F\phi^{\text{s}} } \right)$$

(24)

A rearrangement of Eq. (24), considering that z _Ox − z _Red = n, leads to:

$$\mu_{\text{Ox}}^{\emptyset,{\text{s}}} + n\mu _{\text{e}}^{{\emptyset,{\text{M}}}} -\mu_{\text{Red}}^{{\emptyset,{\text{s}}}} + \frac{RT}{nF}{ \ln }\frac{{a_{\text{Ox}} }}{{a_{\text{Red}} }} = nF\left[ {\left( {\phi^{\text{M}} - \phi^{\text{s}} } \right)} \right]_{\text{eq}}$$

(25)

where $nF(\phi^{\text{M}} - \phi^{\text{s}} )$ is the electrical component of the free energy, i.e. of the work necessary to transfer n electrons across the metal | solution interface.

Equations (24) and (25) establish a relationship between the electrical and the chemical components of the electrochemical free energy at the equilibrium. The electrode potential E is expressed by the Galvani potential difference relative to the electrode metal and the solution phase:

$$E_{{{\text{Ox}}/{\text{Red}}}} = \left( {{{\Delta\phi }}^{{{\text{M}},{\text{s}}}} } \right)_{\text{eq}} = \left[ {\left( {\phi^{\text{M}} - \phi^{\text{s}} } \right)} \right]_{\text{eq}}$$

(26)

Since the standard potential, $E^{\emptyset }$, is defined for $\frac{{a_{\text{Ox}} }}{{a_{\text{Red}} }} = 1$, a standard state for electrical component of the free energy is also defined; it coincides with the standard potential of the redox couple:

$$E_{{{\text{Ox}}/{\text{Red}}}}^{\emptyset} = \mu_{\text{Ox}}^{\emptyset,s} + n\mu_{\text{e}}^{{\emptyset,{\text{M}}}} - \mu_{\text{Red}}^{{\emptyset,{\text{s}}}}$$

(27)

A relationship similar to Eq. (17) may be written for the individual half-cell potentials.

$$RT\,{ \ln }\,K_{{{\text{Ox}}/{\text{Red}}}} = \Delta \tilde{G}_{{{\text{Ox}}/{\text{Red}}}}^{\emptyset } = nFE_{{{\text{Ox}}/{\text{Red}}}}^{\emptyset }$$

(28)

It may be redundant to notice that all quantities in Eqs. (13), (14), and (28) can be only computed in the frame of a cell completed by a reference electrode, e.g. a standard hydrogen electrode, SHE.

The following expression is often used:

$$E_{{{\text{Ox}}/{\text{Red}}}} = E_{{{\text{Ox}}/{\text{Red}}}}^{\emptyset '} + \frac{RT}{nF}\ln \frac{{c_{\text{Ox}} }}{{c_{\text{Red}} }}$$

(29)

where $E_{{{\text{Ox}}/{\text{Red}}}}^{\emptyset '}$ is the formal potential of the Ox/Red couple, i.e. the modification of the standard potential to include the activity coefficients of Ox and Red species and side reaction coefficients accounting for (chemical equilibria of the redox species). In many cases, in fact, it is impossible to calculate the resulting deviations, since neither the thermodynamic equilibrium constants are known, nor it is possible to calculate the activity coefficients [1]. The potential of the cell reaction and the potential of the half-cell reaction are expressed in terms of concentrations.

It is clear that one needs a spontaneous cell reaction, if the aim is to harvest energy. It can be used to produce a sound from a radio, to light an incandescent lamp, to activate a mechanical drive, or—why not—to heat an oven.

On the other hand, in potentiometric measurements,⁷ a similar electrochemical system is built, but flow of current is prevented, except for the negligible extent necessary to make a high-impedance voltmeter work. In a potentiometric setup, with reference to Fig. 1, the switch S is open and R _v tends to ∞; the V voltmeter measures the emf of a cell in which one electrode is the reference and the other is the indicator electrode.

Unified treatment of galvanic and electrolytic cell

At variance with the galvanic cell, in an electrolytic cell, the spontaneous reaction is reversed: making reference to the scheme in Fig. 1, this is achieved by closing the S switch, by inserting the external continuous voltage source, ΔV, and by making R _v tend to ∞. The voltage generator is connected with the two electrodes in such way that the direction of the two reactions, which spontaneously proceed in the galvanic cell, is reversed. This means that the negative pole of the voltage source is connected with that electrode which was the negative pole of the galvanic cell, and the positive pole of the source is connected with the electrode that was the positive pole of the galvanic cell. When the emf of the external voltage source is lower than E _cell, the spontaneous reaction can still proceed and the electrochemical cell determines the direction of the current. For equal values of emf and ΔV, no current flows, and for ΔV higher than emf, the current direction is reversed and electrolysis is taking place. The cell reaction in Eq. (8) is reversed, i.e. a non-spontaneous reaction is forced to proceed: the galvanic cell is turned into an electrolytic cell. A number of changes occur in the electrochemical cell:

• 1. In half-cell 1, electrons are forced to pass from the electrode to Ox₁:

Ox₁ + ne ⇆ Red₁

It is now the cathodic compartment of the cell, but the reduction is not a spontaneous one: it occurs thanks to the negative electrode potential imposed by the external voltage source.

• 2. In half-cell 2, electrons are ‘extracted’ by the electrode from Red₂:

Red₂ ⇆ Ox₂ + ne

It is now an anodic compartment of the cell, but the oxidation is forced by the positive potential imposed by the external voltage source.

• 3. Electrons flow counterclockwise in the external sub-circuit, and ions migrate in direction opposite to those of the galvanic cell in the internal sub-circuit.

• 4. Reaction in Eq. (8) shifts further and further from equilibrium with increasing the applied potential.

Summarising, a cathode is spontaneously positively charged in a galvanic cell and forced to be negatively charged in an electrolytic cell; in any cases, it is always the electrode at which a reduction occurs. On the other hand, an anode is spontaneously negatively charged in a galvanic cell and forced to be positively charged in an electrolytic one, being, however, always the electrode at which oxidation occurs. The different situations are sketched in Fig. 3. Note that in both configurations oxidation occurs at the anode⁸ and reduction occurs at the cathode.

Fig. 3

Anode and cathode in a galvanic and in an electrolytic cell

Fig. 4

Scheme of a two-electrode cell

The relationships hereafter hold for the case of both a galvanic and an electrolytic cell. Let ΔV be the value of the voltage difference between cathode and anode, resulting in ΔV > 0 and ΔV < 0 for a galvanic and for an electrolytic cell, respectively. Let E ₁ and E ₂ be the actual electrode potentials, different from the equilibrium value by the η overpotential, ⁹ either for the occurrence of a spontaneous or of a forced charge transfer. By defining:

$$\eta_{1} = E_{1} {-}E_{{{\text{eq}},1}}$$

(30)

$$\eta_{2} = E_{2} {-}E_{{{\text{eq}},2}}$$

(31)

it follows that, for the single electrode, in any cases:

$$\eta_{\text{anode}} > 0\,\,{\text{and}}\,\,\eta_{\text{cathode}} < 0$$

(32)

η _anode + η _cathode gives the overpotential of the cell as a whole, i.e. the shift of the cell potential, E, with respect to E _cell due to the flow of current

$$\eta = E{-}E_{\text{cell}}$$

(33)

and

$$\eta = \eta_{\text{anode}} + \eta_{\text{cathode}}$$

(34)

The following relationship holds:

$$\pm \Delta V = E_{\text{cell}} \mp \eta \mp iR_{\text{s}} = E \mp iR_{\text{s}}$$

(35)

where upper and lower signs hold for a galvanic and for an electrolytic cell, respectively; iR _s is the so-called ohmic drop in solution.¹⁰

Electrolytic cells. Measurement of the current

It has been pointed out that in electrolytic cells an external voltage source forces the cell process to occur in a non-spontaneous direction. In the amperometric techniques, the attention is devoted to what happens, in terms of current, at an electrode, which is called the working electrode (WE), polarised at a suitable potential or subsequent different potentials. A second electrode is called, quite aptly, the auxiliary electrode (AE) or counter electrode, since its role is only that of closing the electric circuit by providing an electrode where the electrons flow in the opposite direction. Although the extension to different situations is quite easy, it is worth mentioning that we refer here to amperometric techniques in which the WE possesses a quite small surface area. Small current intensities are measured, and small overall electric charges are delivered, so that only meaningless changes in the composition of the solution are caused. The current measurement is typically performed either, at a constant potential, as a function of time (chronoamperometry) or as a function of the potential, which is varied with time (voltammetry). The function according to which the potential is varied with time is defined by the waveform and, concurrently, the characteristics (and the denomination) of the relevant technique: different E(t) functions define different voltammetric techniques.

It is clear from Eq. (35) that in the electrolytic cell depicted, when ΔV is applied between the two electrodes, the individual electrode potential values are not known. The value of E _cell may be known by a suitable potentiometric measurement. On the other hand, the term iR _s may be either minimised, down to a negligible value, or even computed by measuring R _s with an impedance bridge; η is, hence, computed, but it cannot be separated into the two individual components, i.e. η _anode and η _cathode, respectively. η _anode and η _cathode constitute the extent of the shift of the actual anode and cathode potentials from the relevant equilibrium values, as expressed by Eqs. (30) and (31), respectively. They are necessary to perform a forced oxidation and reduction, respectively. The question is hence: How is the overall overvoltage, η, subdivided into the energies acting on the reaction at the anode and at the cathode, respectively?¹¹

In a two-electrode scheme (see Fig. 4), the only possibility to know what is of interest is achieved by minimisation of |η _AE|, so that the overall overvoltage η is practically identical with η _WE.

This goal may be pursued, to a first approximation, by using an AE possessing a much larger surface area than the WE. The extent of polarisation of an electrode, i.e. the deviation from the equilibrium electrode potential, is a function of the current density (j), i.e. the current flowing per unit electrode area, rather than of the overall current. Since the WE area in the amperometric techniques is much smaller than the area of the AE, the same absolute current flowing at both electrodes implies a much lower current density at the AE than on WE: the shift of the AE potential from the equilibrium value is much smaller, i.e. |η _AE| ≪ |η _WE|, so that η _WE ≈ η.

However, the use of an AE with a large surface area is only of rather limited effect in making η _WE approximately known. The three-electrode circuit (see Fig. 5) represents a definite step forward to the accurate knowledge of the actual WE potential.

Fig. 5

Scheme of a three-electrode cell

In correspondence with ΔV imposed between WE and AE, belonging to the ‘main circuit’, the potential difference between the WE and a reference electrode (RE) is measured in an additional circuit, with a high-impedance voltmeter that prevents the current from assuming meaningful values. The current flowing in the WE-AE circuit is recorded as a function of the potential measured in the WE-RE one. The voltage source supplies the ΔV voltage necessary for the WE-AE potential difference to assume the required value. Noteworthy, RE is a poorly polarisable electrode, such as the already mentioned SCE, or an Ag/AgCl, Cl⁻ one (see footnote 9) [1, 17].

A three-electrode circuit, possessing a suitable geometry as to location, shape, and size of the three electrodes, allows the actual WE potential to be known with satisfactory accuracy. However, the RE is inside the electric field generated by the WE-AE circuit, in a point obviously different from that in which WE is located: an inner potential difference exists between the two points of the solution phase to which Δϕ _RE and Δϕ _WE make reference. In other words, the ϕ value of the solution phase where RE is located is different from that where WE is, to a Δϕ extent: the potential difference measured between WE and RE also includes this Δϕ, which is called the uncompensated ohmic drop (iR _u ). RE may be inserted in a compartment containing both solvent and electrolyte at a high enough concentration, ending with a capillary (Luggin or Haber-Luggin capillary), in which no current flows, and hence, no ohmic drop occurs, so that the potential at the RE coincides with that at the end of the capillary. This allows the RE to be located very close to the WE surface, without interfering significantly with phenomena in solution induced by the current flow, such as the mass transfer to and from the electrode. The resulting three-electrode cell finally looks as reported in Fig. 6. Use of a Luggin capillary is important when the solution has a low conductivity and when the currents between the WE and the AE are large. In analytical measurements, this is rarely necessary. On the other hand, in mechanistic studies typical of so-called molecular electrochemistry, amperometric techniques are often used in such conditions that relatively high currents are measured. At the same time, highest possible precision in the measures is required: a proper cell geometry, i.e. areas and reciprocal locations of the three electrodes assuring constant potential at any points of WE, and as low as possible ohmic drop between WE and RE, are mandatory.

Fig. 6

A three-electrode cell

Electronic tools (positive feedback, current interrupt) are available in electrochemical instrumentation for amperometric techniques, in order to insert a correction accounting for the ‘uncompensated ohmic drop’. Correction by software of the potential measured by the voltmeter, once the solution resistance between RE and WE is measured, is also possible. The measured current allows the construction of a potential scale that reflects the values actually assumed by the WE.

A large variety of different electrode mechanisms may be operative: preceding and follow-up chemical reactions as well as adsorption of educts or products may happen, and multistep electron transfer reaction may occur. The mass transfer to and from the electrode of species Ox and Red, respectively, constitutes a process that is, in all cases, in series with the charge transfer. Mass transfer will not be considered at the moment, assuming that the concentrations of electroactive species at the electrode are given by the Nernst equation or by the kinetics of the charge transfer: Ox and Red species at the electrode are affected by nothing else than the rate of the charge transfer, excess or deficiency of Ox or Red species at the electrode being ignored. This means that indicating with x the distance from the electrode surface, and with $c_{\text{Ox}}^{*}$ and $c_{\text{Red}}^{*}$ the concentrations in the ‘bulk’ of the solution, i.e. at a distance from the electrode at which the concentrations are not significantly altered by the electrode reaction, in any cases, it holds that c _Ox(x = 0) = $c_{\text{Ox}}^{*}$ and c _Red(x = 0) = $c_{\text{Red}}^{*}$. Furthermore, we will consider here the case of the so-called uncomplicated charge transfer, where a simple n electron charge transfer occurs, involving species soluble and stable in the solution phase. An oxidation reaction is considered as an example:

$${\text{Red}} \leftrightarrows {\text{Ox}} + ne$$

(36)

Our attention is, hence, limited to the transfer of n electrons to the electrode from the Red species in solution, in the close proximity of the surface itself. No consideration is made as to what happens further, at the moment.

Electrode kinetics

In line with the foregoing discussion, we like to emphasise that the rate of this n electron charge transfer depends on the rate of the slowest step, which is mostly a single electron charge transfer. In other words, the whole kinetics of the anodic oxidation or cathodic reduction in a species is conditioned by a one-electron charge transfer; the additional eventual electrons exchanged in the overall process increase the extent of the current flowing, though not conditioning the rate of the process. In this frame, the current may result coincident or higher than predicted by the rate of the charge transfer: a nF proportionality factor links rate to current.

As anticipated in the first lines of this contribution, a fascinating aspect of electrochemistry is the fact that one can affect with the electrode potential both the redox equilibrium (thermodynamics) and the rate of the reduction and oxidation reactions.

The relative energy levels of reactants and products may be changed by changing the electrode potential, acting consequently on the value of the equilibrium constant for reaction in Eq. (8), i.e. affecting the thermodynamics of the system. Furthermore, at variance with what happens in the chemical kinetics, in which the plots of the standard free energy versus reaction coordinates are usually only parametric in pressure and temperature; in electrode kinetics, the electrode potential plays a fundamental role.

It is worth noticing that, similarly to the redox reactions occurring in a homogeneous solution, outer and inner sphere mechanisms are distinguished also for oxidations and reductions occurring at an electrode that are affected by charge transfer overvoltages. In this case, of course, one of the partners of the redox reaction is the electrode itself. This causes that different electrode materials may present significantly different charge transfer overvoltages for reactions occurring via an inner sphere charge transfer. Figure 6 gives a sketch of the two different interactions between electroactive species and electrode.

Considering the oxidation or reduction reaction involving the Ox/Red couple, in principle, the rate of the oxidation reaction in Eq. (36) is given by the vector sum of forward (oxidation) and backward (reduction) reactions of the slowest oxidation step, assumed here to involve one electron, according to what has been discussed above:

$$\vec{v}\left( t \right) = \vec{k}_{{{\text{h}},{\text{f }}}} c_{\text{Red}} \left( {x = 0;t} \right) + \vec{k}_{{{\text{h}},{\text{b}}}} c_{\text{Ox}} \left( {x = 0;t} \right)$$

(37)

where $\vec{k}_{{{\text{h}}.{\text{f}}}}$ and $\vec{k}_{{{\text{h}},{\text{b}}}}$ indicate the relevant heterogeneous rate constants, whereas c _Red and c _Ox are the concentrations of the species in the reduced and in the oxidised form, respectively. Their values have to be considered at the distance from the electrode at which charge transfer takes place, chosen as the origin of the distance coordinate (x = 0). With reference to Fig. 7, the OHP may identify the limit, in the solution phase, of the so-called electrical double layer, i.e. the layer within which molecules and ions of the solution assume a structure different from that in the bulk of the solution. It should be kept in mind that, according to the double-layer theory, the potential and composition changes are confined to ca. 1 nm in concentrated electrolytes, while they can extend to several tens of nm in dilute ones. The variable t is inserted from Eq. (37) onwards, in order to account for possible dependence of the rate (and of the consequently flowing current) on time, due to possible changes in concentration of the electroactive species at the electrode. Since the reaction occurs at the electrode|solution interface, v is expressed as mol cm⁻² s⁻¹; since mol cm⁻³ are the units of c, the kinetic constants are expressed in cm s⁻¹. The direction of the rate vectors is the same, the sign being, however, opposite, so that scalar quantities with opposite sign are suitable to express the net rate.

Fig. 7

Schemes of outer and inner sphere charge transfers at an electrode. GC glassy carbon. The broken line crossing the iron ions or complexes identifies the so-called Outer Helmholtz Plane (OHP). From Ref. [18] with permission of the American Chemical Society

Moreover, in order to express the rate of the process in terms of current, one possible statement of the Faraday’s law of electrolysis should be used:

$$Q = nFn_{\text{mol}}$$

(38)

where Q indicates the number of Coulomb (C) spent during the electrochemical process; as already specified, the units of F are C mol⁻¹. Once n _mol is the number of mol reacted per unit electrode area, expressed in mol cm⁻², the unit for Q is C cm⁻². The corresponding current density:

$$j = {\text{d}}Q/{\text{d}}t$$

(39)

results expressed in C cm⁻² s⁻¹, assuming that a normalisation with respect to the electrode surface area is performed, as required by the definition of j. The commonly used unit for j is Amperes per unit area, A cm⁻², so that the relationship:

$$j\left( t \right) = nFv\left( t \right)$$

(40)

where n is the number of electrons that are exchanged as a whole, as a consequence of the occurrence of the reactions accounted for by Eq. (37) (see below and note¹² for better comprehension of underlying arguments): Eq. (40) constitutes the well-known relationship between current density and reaction rate, once the above-specified, proper units are ascribed to v(t).

According to the accepted convention, a positive sign is ascribed to the anodic current:

$$j\left( t \right) = nF\left[ {k_{\text{h,f}} c_{\text{Red}} \left( {0;t} \right){-} \, k_{\text{h,b}} c_{\text{Ox}} \left( {0;t} \right)} \right]$$

(41)

where k _h,f and k _h,b, are the kinetic rate constants for forward (oxidation) and backward (reduction) reactions, respectively.

It is well known from the chemical kinetics that a plot of the standard Gibbs free energy versus the co-called reaction coordinates accounts for the energy content of the system in passing from the reactants to the products and vice versa. The energy content of the initial and final states defines the thermodynamics of the reactants/products system, as expressed by numerous equations reported in this article. The intermediate states account for the energy content along the reaction path followed, referred to a suitable parameter describing the evolution of the system. This can consist of the distance between reacting species, of the value of a bond length or of a bond angle that changes in a reacting molecule, or of anything capable to quantitatively account for the progress of the reaction. In some cases, a suitable expression, including more or even all changing parameters, is used.

In few cases, the trend of the energy content of the intermediate systems is monotonic in character—see, for example, breaking and formation of the I–I bond in the iodine molecule leading to or forming from iodine atoms. In some cases, the plot presents one or more relative maxima. For the sake of simplicity, let’s consider the case of a reaction path that only implies one relative maximum: the geometry and free energy content in correspondence with the maximum define the so-called transition complex or activated complex. The free energy required by one mole of the reactant in the standard state to achieve the top of the energy hill constitutes the activation standard free energy for the reaction in one $(\Delta G_{\text{f}}^{\emptyset \# } )$ or in the opposite direction $(\Delta G_{\text{b}}^{\emptyset \# } )$; the whole plot defines both the thermodynamics (energy difference between reactants and products) and the kinetics of the process. In chemical kinetics, the plot only depends on temperature and pressure.

On the contrary, the electrical component of $\tilde{\mu }$, in addition to condition of the relative stability of oxidised and reduced forms of the Ox/Red redox couple, also affects the energetics of the transition from one to the other partner of the couple involved in the charge transfer. It follows that the electrode kinetics is accounted for by a plot of electrochemical free energy $\tilde{G}$ versus reaction coordinates; it results from the sum of a molar chemical standard free energy with a molar electrical free energy G _e versus reaction coordinate plot. For a given Ox/Red system, there are infinite possible plots of the electrical component, corresponding to infinite number of possible potential values assumed by the electrode. The equilibrium and the conversion rate of Red to Ox and vice versa may be, in principle, tuned of your choosing. Figure 8 reports a triad of the discussed plots, relative to an equilibrium or non-equilibrium potential, assumed by or imposed to the electrode at which the charge transfer takes place.

Fig. 8

The whole energetics of the charge transfer in the text (upper plot), as the sum of the chemical component (middle plot) and an electrical component (bottom plot)

Noteworthy, the values of electrical free energy by passing from Red to Ox follow a monotonic trend (Fig. 8). The value of the charge transfer coefficient, α [21], fixes the fraction of ${{\Delta }}\phi$ ($\alpha F{{\Delta }}\phi$—bottom plot in Fig. 8) that should be added to or subtracted from the chemical standard activation free energy for the reaction in one direction, $\Delta G_{\text{c,f}}^{\emptyset \# }$ (see middle plot in Fig. 8), to obtain the electrochemical activation free energy (upper plot in Fig. 8). A (1 – α)$F{{\Delta }}\phi$ energy should be subtracted or added, respectively, for the reaction in the opposite direction. In the case of an oxidation reaction, the more positive ${{\Delta }} \phi$ the higher the contribution of the electrical component to speed up the forward reaction, the more negative ${{\Delta }}\phi$ the higher the contribution of the electrode potential to speed up the reverse reaction, according to the following linear free energy relationships:

$$\Delta G_{\text{e,f}}^{\# } = - \alpha F\Delta \phi$$

(42)

and

$$\Delta G_{\text{e,b}}^{\# } = \left( {1 - \alpha } \right)F\Delta \phi$$

(43)

where $\Delta G_{\text{e,f}}^{\# }$ and $\Delta G_{\text{e,b}}^{\# }$ indicate the electrical contribution [see Eq. (5)], in terms or activation energy, of the electrode potential to forward (oxidation) and to backward (reduction) reaction, respectively. As a further consideration, it is experimentally verified that α varies in the very most cases within the range 0.3 ÷ 0.7, resulting often close to 0.5. This allows discarding limiting situations in which the conformation and, consequently, the electronic state of the transition complex are too similar to that of the reactant or of the product.

The differences between the energy of the relative maximum and those of reactants and products in the plot of Fig. 8 are expressed by:

$${{\Delta }}\tilde{G}_{\text{f}}^{\# } = {{\Delta }}G_{{{\text{c}},{\text{f}}}}^{\emptyset \# } - \alpha F{{\Delta }}\phi$$

(44)

and

$${{\Delta }}\tilde{G}_{\text{b}}^{\# } = {{\Delta }}G_{{{\text{c}},{\text{b}}}}^{\emptyset \# } + \left( {1 - \alpha } \right)F{{\Delta }}\phi$$

(45)

where ${{\Delta }}\tilde{G}_{\text{f}}^{\# }$ and ${{\Delta }}\tilde{G}_{\text{b}}^{\# }$ indicate the electrochemical activation free energy for forward (oxidation) and backward (reduction) charge transfer, respectively, $\Delta G_{{{\text{c}},{\text{f}}}}^{\emptyset\# }$ and $\Delta G_{{{\text{c}},{\text{b}}}}^{\emptyset\# }$ are the corresponding standard chemical components of the Gibbs free energy of activation of the reaction, and, for the sake of simplicity, ${{\Delta }}\phi$ is used from here onwards to indicate ${{\Delta }}\phi^{{{\text{M}},{\text{s}}}}$.¹³ On the basis of Eqs. (44) and (45), the rate constants that give reason of the actual rate of the charge transfer, i.e. of the current flowing, are given by:

$$k_{{{\text{h}},{\text{f}}}} = \frac{{k_{B} T}}{h}\exp \left[ { - \frac{{\Delta \tilde{G}_{\text{f}}^{\# } }}{RT}} \right] = k_{{{\text{c}},{\text{f}}}} {\text{exp }}\left[ {\frac{\alpha F\Delta \phi }{RT}} \right]$$

(46)

and

$$k_{{{\text{h}},{\text{b}}}} = \frac{{k_{B} T}}{h}\exp \left[ { - \frac{{{{\Delta }}\tilde{G}_{\text{b}}^{\# } }}{RT}} \right] = k_{{{\text{c}},{\text{b}}}} \,{\text{exp }}\left[ {\frac{{-\left( {1 - \alpha } \right)F{{\Delta }}\phi }}{RT}} \right]$$

(47)

where $k_{B}$ and $h$ are the Boltzmann and Planck constants, respectively. Equations (46) and (47) account for both chemical and electrical contributions to the charge transfer kinetics. Hence, every term in Eq. (41) has been defined. An alternative expression of the current density is possible:

$$j\left( t \right) = nF\left\{ {\frac{{k_{B} T}}{h}\exp \left[ { - \frac{{{{\Delta }}\tilde{G}_{\text{f}}^{\# } }}{RT}} \right] c_{\text{Red}} \left( {0;t} \right) {-} \frac{{k_{B} T}}{h}\exp \left[ { - \frac{{{{\Delta }}\tilde{G}_{\text{b}}^{\# } }}{RT}} \right] c_{\text{Ox}} \left( {0;t} \right)} \right\}$$

(48)

Based on the expression for the chemical kinetic constant, fictitiously ‘extracted’ from the actual constant defined in Eqs. (46) and (47):

$$k_{{{\text{c}},{\text{f}}}} = \frac{{k_{B} T}}{h}\exp \left[ { - \frac{{{{\Delta }}G_{{{\text{c}},{\text{f}}}}^{\emptyset \# } }}{RT}} \right]$$

(49)

and

$$k_{{{\text{c}},{\text{b}}}} = \frac{{k_{B} T}}{h}\exp \left[ { - \frac{{{{\Delta }}G_{{{\text{c}},{\text{b}}}}^{\emptyset \# } }}{RT}} \right]$$

(50)

which are common expressions for chemical kinetic constants. A further expression for the current density can be written, in which the dependence on the electrode potential is explicit:

$$j\left( t \right) = nF\left\{ {k_{{{\text{c}},{\text{f}}}} \exp \left[ {\frac{{\alpha F{{\Delta }}\phi }}{RT}} \right] c_{\text{Red}} \left( {0;t} \right) - k_{{{\text{c}},{\text{b}}}} \exp \left[ {\frac{{-\left( {1 - \alpha } \right)F{{\Delta }}\phi }}{RT}} \right] c_{\text{Ox}} \left( {0;t} \right)} \right\}$$

(51)

In the particular situation of E = E _eq, i.e. at Δϕ = (Δϕ) _eq (see Fig. 11 in the following), j(t) = 0 which implies that j _f(t) = j _b(t). The so-called exchange current density is defined by:

$$j_{0} \left( t \right) = nFk_{\text{c,f}}\ c_{\text{Red}} (0;t)\,{ \exp}\left[{\frac{{\alpha F(\Delta \phi )_{\text{eq}}}}{RT}}\right] = nFk_{\text{c,b}}\ c_{\text{Ox}} \left( {0;t} \right)\,{ \exp}\left[{\frac{{- (1 - \alpha )F(\Delta \phi )_{\text{eq}}}}{RT}}\right]$$

(52)

i.e.:

$$j_{0} \left( t \right) = j_{\text{f}} \left( t \right) = j_{\text{b}} \left( t \right)$$

(53)

Since it holds that

$$E = E_{\text{eq}} + \eta$$

(54)

and recalling that a positive value for η favours the oxidation reaction considered in our example, it follows from Eqs. (51) and (52) that

$$j\left( t \right) = j_{0} \left( t \right)\left\{ { \exp }\left[{\frac{{\alpha F{\eta }}}{RT}} \right] { \, - { \exp }} \left[ {\frac{-\left( {1 - \alpha } \right)F\eta}{RT}}\right]\right\}$$

(55)

The value of the exchange current density accounts for the degree of reversibility of the charge transfer: the higher j ₀(t) the higher the degree of reversibility of the charge transfer. As shown in Fig. 9, the higher j ₀(t), the smaller |η | values are required to make a given anodic or cathodic current flow.

Fig. 9

Equation (55) is plotted for two charge transfers very different as to degree of reversibility. c_Ox(0;t) and c_Red(0;t) assume constant values, independent of the η value

j ₀(t) accounts the dynamic character of the charge transfer. It is not directly measurable electrochemically, since it flows with equal intensity in opposite directions at E = E _eq; as already evidenced, the net current density, j(t), equals 0. It can be determined by extrapolation from the current values measured at potentials more positive or negative with respect to E _eq, to such an extent to be suitable to make one of the two terms in Eq. (55) negligible, in the so-called Tafel plot:

$$j\left( t \right) = j_{0} \left( t \right)\left\{ { \exp }\left[ {\frac{{\alpha F{\eta }}}{RT}} \right]\right\}$$

(56)

i.e.

$${ \ln }\,j\left( t \right) = { \ln }\,j_{0} \left( t \right) + {\frac{{\alpha F{\eta }}}{RT}}$$

(57)

and

$$j\left( t \right) = j_{0} \left( t \right)\left\{ { \exp }\left[ {\frac{-\left( {1 - \alpha } \right)F\eta}{RT}}\right]\right\}$$

(58)

i.e.

$${ \ln }\,j\left( t \right) = { \ln }\,j_{0} (t) -{\frac{\left( {1 - \alpha } \right)F\eta}{RT}}$$

(59)

The Tafel plot in Fig. 10 accounts for the Tafel Eqs. (58) and (60).

Fig. 10

Tafel plot for anodic and cathodic portions of the j versus η curve [see Eqs. (57) and (59)]. α = 0.5, T = 298 K, j ₀  = 10⁻⁶ A cm⁻². Adapted from Ref. [12]

In summary, the determination of the transfer coefficient requires the experimental measurement of the Tafel slope. Since many electrode reactions involve the participation of more than one electron, their mechanistic investigation should include different elementary one-electron transfer steps in the reaction scheme. In the case of a multistep electrode reaction, the quasi-equilibrium or the steady state method can be applied. In the case of the quasi-equilibrium method, it is assumed that all the steps except the rate determining one are in equilibrium.

The term of symmetry factor β is also used. It is the transfer coefficient for a one-electron transfer step. In the case of a symmetric potential energy barrier, β = 0.5.

It is possible to define a parameter, characterising the degree of reversibility of the charge transfer and to draw out a relationship between the standard electrode potential (standard electrical free energy) and the relevant chemical counterpart.

If

$$c_{\text{Ox}} \left( {0;t} \right) = c_{\text{Red}} \left( {0;t} \right) \Rightarrow E = E^{\emptyset '} \Rightarrow j\left( t \right) = 0 \Rightarrow j_{\text{f}} \left( t \right) = j_{\text{b}} \left( t \right)$$

(60)

In view of Eqs. (48), (44), and (45), it holds that

$$k_{\text{h,f}} = k_{\text{h,b}} \,\,{\text{and}}\,\,{{\Delta }}\tilde{G}_{\text{f}}^{\emptyset \# } = \Delta \tilde{G}_{\text{b}}^{\emptyset \# }$$

(61)

Equal electrochemical standard free energies are proper of reactants and products at E = $E^{\emptyset '}$, implying that

$$\left( {\Delta \tilde{G}^{\emptyset } } \right)_{{E = E^{\emptyset '} }} = 0$$

(62)

It follows that a common standard heterogeneous kinetic rate constant k _s,h is defined for both forward and backward charge transfers:

$$k_{\text{s,h}} = k_{\text{c,f}}\, { \exp }\left[{\frac{{\alpha FE^{\emptyset '}}}{RT}}\right] = k_{\text{c,b}}\, { \exp }\left[{\frac{-\left( {1 - \alpha } \right)FE^{\emptyset '}} {RT}}\right]$$

(63)

A positive shift from E°’ obviously favours the forward oxidation and vice versa as to the backward reduction. Combining Eqs. (63) and (51):

$$j\left( t \right) = nFk_{\text{s,h}}\left \{ c_{\text{Red}} \left( {0;t} \right){ \exp }\left[{\frac{{\alpha F(E - E^{\emptyset '} )}}{RT}}\right]{-}{\text{c}}_{\text{Ox}} \left( {0;t} \right){ \exp }\left[{\frac{{- \left( {1 - \alpha } \right) F(E - E^{\emptyset '} )}}{RT}}\right]\right\}$$

(64)

Very importantly, k _s,h accounts for the degree of reversibility of the charge transfer.

Equations (55) and (64) are possible forms of the Erdey-Grúz–Volmer (or Butler–Volmer) (see footnote 12) equation.

Figure 11 reports the kinetic plots for charge transfers possessing different degree of reversibility: different k _s,h and different j ₀ values correspond to different ${{\Delta }}\tilde{G}_{\text{f}}^{\emptyset \# } = {{\Delta }}\tilde{G}_{\text{b}}^{\emptyset \# }$. Comparing the quantities reported in the ordinate axis in the plots in Fig. 10, it is evident that electrical and, consequently, electrochemical standard free energies may be only defined in this case, i.e. for E = $E^{\emptyset}$.

Fig. 11

Plots similar to those in Fig. 7, relative to different degree of reversibility of the charge transfer, are shown for the particular case of E = $E^{\emptyset'}.$ Arrows indicate the direction along which curves with progressive increase in the degree of reversibility are found

Noteworthy, curves on Fig. 11 refer to ideally reversible charge transfer:

$${{\Delta }}G_{{{\text{c}},{\text{f}}}}^{\emptyset \# } = {{\Delta }}G_{{{\text{c}},{\text{b}}}}^{\emptyset \# } = 0$$

(65)

Incidentally, let’s notice that the plots in Fig. 11 give account of the relationship:

$${{\Delta }}G_{\text{c}}^{\emptyset } = nFE^{\emptyset }$$

(66)

which is nothing else than Eq. (28).

As it is evident from the plots in Fig. 11, as well as from the different expressions for the Erdey-Grúz–Volmer equation, in which both c_Ox(0;t) and c_Red(0;t) are kept constant, whatever the η value, in all cases the current density tends to unrealistic (even impossible) high values for high enough overvoltages. It is easy to verify that at increasing the degree of reversibility, this happens for not so big shifts of E from $E^{\emptyset}$.

It is evident that this constitutes an unrealistic situation because the physical model does not account for the mass transfer limitations, arising when the charge transfer rate exceeds certain limits. The electrode kinetics should be complemented by mass transfer, occurring as a consequence of the charge transfer.

The rest of the story dealing with an uncomplicated charge transfer with both the involved species soluble in solution requires the consideration of how the perturbation arising at the electrode by the charge transfer propagates into the solution. In principle, different mass transfer mechanisms are operative in the transport of reacting species to the electrode and of the product away from the electrode. However, depending on the specific amperometric technique adopted, carefully controlled conditions for the mass transfer processes are sought; this is essential in order to perform reproducible tests leading to reproducible responses, as well as to make a reliable comparison with the theoretical responses. Such an agreement with theory is not only mandatory in the case of mechanistic studies, such as those performed in molecular electrochemistry, but also in electroanalysis and in preparative electrochemistry. It is intention of the authors to deal extensively with the mass transfer mechanisms and related issues in a next contribution to this same publication.