1 Introduction

R&D is key to long-term success in many industries such as the pharmaceutical sector. However, effectively allocating resources to the most valuable R&D project(s) is challenging (Hartmann and Hassan 2006). Valuing (sequential) R&D projects has thus received much attention in academia and corporate practice (e.g., Amram et al. 2006; Cassimon et al. 2011a; Nichols 1994). In this regard, it is well acknowledged among researchers and practitioners that R&D investments represent real options to the investing firm (Huchzermeier and Loch 2001; Koussis et al. 2013; Pennings and Lint 1997; Perlitz et al. 1999). As such, R&D projects typically do not lead to immediate cash flows but open up further investment opportunities. Traditional valuation methodologies fail to capture this option-like flexibility though (Bowman and Moskowitz 2001; Pennings and Lint 1997). Consequently, calculating real option values and incorporating these values when analyzing whether to fund the respective investments has been called for in the academic literature for decades (Denison et al. 2012).

Albeit this potential of real options valuation, numerous studies have shown that many firms do not explicitly incorporate the real options approach in allocating R&D resources (e.g., Baker et al. 2011; Bennouna et al. 2010; Block 2007; Graham and Harvey 2001). However, in some industries like the pharmaceutical sector, real options analysis seemingly found its place in the method set as an auxiliary valuation tool:Footnote 1 Hartmann and Hassan (2006), in their study of leading international research-based pharmaceutical and biotech companies, find that roughly one quarter of the surveyed R&D managers use real options analysis as a valuation method. Among the obstacles to more widespread adoption of real options analysis, the complexity of option pricing models and a perceived lack of transparency stand out (Hartmann and Hassan 2006, for further evidence, see Baker et al. 2011; Bowman and Moskowitz 2001; Lander and Pinches 1998). Thus, continuous-time analytical option pricing models in particular are characterized by “low practical validity” (Worren et al. 2002) because of their advanced, intransparent valuation algorithms (Lander and Pinches 1998; Triantis 2005). Consequently, Hartmann and Hassan (2006: 353) emphasize that “academia is challenged to develop more adequate models to boost acceptance,” and they emphasize the potential of binomial approaches. Binomial real options approaches do not require sophisticated continuous-time stochastic calculus (Lander and Pinches 1998) but allow scenario planning techniques to be integrated to determine possible development paths for the value of the underlying R&D project (Alessandri et al. 2004; Miller and Waller 2003). As scenario planning is one of the most common long-term planning tools in corporate practice, binomial approaches have the potential to be implemented in corporate practice. In this paper, we therefore propose a binomial compound real options approach to modeling sequential R&D investments that typically require a series of more than two irreversible investments. We increase the practical validity of current compound option models by simplifying the existing valuation methodology (see Copeland and Antikarov 2001; Copeland et al. 2005; Mun 2006). Specifically, based upon the same set of assumptions as prior models, we show that the number of computational steps for valuing a z-fold compound option can be reduced from z steps to just a single step. Our work thus provides a heuristic framework for fostering the adoption of binomial compound option valuation techniques in R&D management. However, we have to note that in the case of R&D, no (perfect) market for trading such a unique “asset” exists. This is an inherent limitation of the binomial compound option valuation technique that needs to be considered when applying the methodology in corporate practice.

We demonstrate the applicability of our approach using the real-world example of valuing a new drug application (NDA), building upon empirical data from the typical drug development process presented in Kellogg and Charnes (2000). This example has been used in various prior papers that mostly chose an analytical approach to modeling compound real options (e.g., Cassimon et al. 2004; Cassimon et al. 2011b). Thus, we can compare our approach to existing models and assess the practical validity of the different approaches.

The remainder of this paper is structured as follows. In Sect. 2, we present the Kellogg and Charnes (2000) example and we outline how such sequential R&D investments can be modeled as compound options, before we finally present our binomial model. In Sect. 3, we apply this approach to valuing the NDA as presented in Kellogg and Charnes (2000). Finally, in Sect. 4, we discuss the practical validity of our approach, we present conclusions, and we outline avenues for future research.

2 Modeling sequential investment decisions as compound options

2.1 Applying binomial option pricing methodology to sequential R&D investments

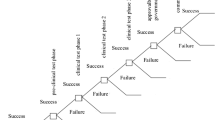
To further illustrate the problem of valuing sequential R&D projects, we refer to the example presented in Kellogg and Charnes (2000), which has received wide attention in academia and, for example, was analyzed by Cassimon et al. (2004). The Kellogg and Charnes (2000) example describes the 6-stage R&D process of a real-life biotechnology company (i.e., Agouron Pharmaceuticals). Figure 1 outlines the progress of the R&D stages and summarizes the most important valuation parameters obtained from Kellogg and Charnes (2000). The R&D project consists of a discovery phase (1 year), a preclinical phase (3 years), three clinical phases I to III (1, 2, and 3 years, respectively), and the FDA filing phase (2 years). The total time to a possible approval is thus 12 years. During those 12 years, typically no revenues occur. The total costs (i.e., investments) incurred in each phase are depicted in Fig. 1 (note that all values are in thousand US$). They represent real-life data collected by Kellogg and Charnes (2000).Footnote 2 In the discovery phase, cost primarily incurs for chemists and biologists developing concepts for synthesizing new molecular entities. In the preclinical phase and the subsequent clinical trial I–III, costs incur for testing the drugs on animals and humans. In the final pre-approval phase, cost incurs for submitting the NDA to the US Food and Drug Administration (FDA) for review. In the subsequent post-approval phase, the company receives revenues from selling the new drug while additional costs (e.g., marketing, product extensions) are incurred. This allows calculating post-approval cash flows. The uncertain possible net payoff values from commercialization are also depicted in Fig. 1. For deriving these payoff values, Kellogg and Charnes (2000) present a scenario analysis for the development of future post-approval cash flows, assuming that a drug reaching the market would fall into one of the categories presented in the work of Myers and Howe (1997). In their study, the (reasonable) investment for the commercialization depends on the expected (gross) payoff of the R&D project. Therefore, Fig. 1 depicts the expected net payoffs from commercialization after (scenario-specific) investments. Cash flows are then discounted to time t = 12 assuming a discount rate of 12.9 %, again following Myers and Howe (1997).

Fig. 1
figure 1

Example of sequential R&D investment

Full size image

This example shows that R&D investments are often sequential and thus typically require a series of more than two irreversible investments, while significant positive project cash flows are realized only when the project is complete (also see Majd and Pindyck 1987). The first investment made to initiate the project can be interpreted as an option premium as it opens up the opportunity to make further investments depending on the progress of the project. On the one hand, sequentiality offers increased flexibility to dynamically allocate resources depending on how the R&D project develops (i.e., how uncertainty resolves) over time (e.g., Klingebiel and Adner 2012). On the other hand, sequentiality also increases the complexity of the decision problem: In the case of failure, the R&D project can be abandoned at any time, but if the project prospers over time, further resources can be allocated, and budgets can also be increased (e.g., Gong et al. 2011). On the methodological level, this implies that simply adding up the isolated values of the option rights inherent in a single R&D project can result in significant misevaluation (Trigeorgis 1993). Instead, sequential R&D investment projects comprising a series of more than just two payments have to be valued as compound real options, that is, options on options (Cassimon et al. 2004; Lee et al. 2008; Pennings and Sereno 2011). We focus exclusively on compound call options as they mirror the iterative multistage R&D management decision process (Crama et al. 2013; Ghosh and Marvin 2012; Kort et al. 2010) and are thus the most appropriate for modeling sequential R&D investments.

Option pricing models are based on a perfect market assumption (Black and Scholes 1973; Cox et al. 1979). However, when applying option pricing techniques to real investment problems, the perfect market assumption does not hold. For example, in the case of R&D, investments are undertaken in order to achieve an innovation. Consequentially, no (perfect) market for trading such a unique “asset” exists. This, of course, is an inherent limitation of the real options approach that needs to be carefully reflected when applying the methodology in corporate practice. However, we still refer to the example of R&D for several reasons: First, this limitation exists for any real investment problem under uncertainty that can be modeled as a real option. Examples include among others IT infrastructure investments (e.g., Panayi and Trigeorgis 1998), venture capital (e.g., Davis et al. 2004), and exploration projects (e.g., Paddock et al. 1988). Second, R&D is still the most prominent application of the real options approach in corporate practice and academic literature. We can thus build on a well-established stream of research and are able to link our results to prior work. Finally, prior research has investigated how the violation of the perfect market assumption affects the model results. Most importantly, on incomplete markets no asset exists that perfectly correlates with the value of the investment project under consideration. In this case, a highly correlated asset can serve as a surrogate when forming a duplicating portfolio (Paddock et al. 1988). The calculated option value thus represents an upper boundary of the investment project value. Still, this can be considered valuable information for corporate decision making (Nau and McCardle 1991; Liu 2010). We thus argue that applying option pricing techniques to valuing sequential R&D investments is a worthwhile approach.

Option pricing models are commonly classified as either continuous-time (closed-form solution) models such as the seminal work of Black and Scholes (1973) and Geske (1979) or discrete-time models such as Cox et al. (1979) and Rendleman and Bartter (1979). Continuous-time models assume a continuous stochastic process for the development of the investment project under consideration and require advanced mathematical calculus such as partial differential equations to determine the final project value. In addition to the complexity of the valuation algorithm, applying analytical models to real options assumes the continuous trading of the underlying asset (i.e., the R&D project) to dynamically duplicate the payoff. While a dynamic programing approach can mitigate tradability constraints, it is difficult to apply in many real-life situations when, for example, the number of state variables is high. In this case, numerical-lattice approaches constitute more practical approaches to valuation (Tr igeorgis 1996). However, discrete-time models require adjustments of the duplicating portfolio only at discrete points in time. Reevaluations of R&D projects are also usually made at equidistant points in time, e.g., on a quarterly, semiannual, or annual basis, which may represent the discrete points in time where the duplicating portfolio is adjusted. Discrete-time real options models thus provide a suitable framework for valuing sequential R&D investment decisions. However, the use of discrete-time models comes at the cost of imposing a simplified (e.g., binomial) distribution of the asset value.

A prominent subcategory of discrete-time models is binomial option pricing models that consider two distinct possible outcomes for the R&D project in every (sub-) period (see Cox et al. 1979; Rendleman and Bartter 1979). Reducing the number of possible states in each period to two states is a simplification of the (real) valuation problem that comes at the cost of reducing the analysis to only one source of uncertainty. However, a common distinction of sources of uncertainty in the literature on valuation of R&D or new product development (NPD) is the distinction between market uncertainty and technical uncertainty (e.g., Cassimon et al. 2011a). Market uncertainty usually resolves over time, whereas technical uncertainty can only be reduced by undertaking the project. Therefore, technical uncertainty does not generate a value of waiting to invest. Modeling technical and market uncertainty, Schneider et al. (2008), for example, assume a lognormal distribution for the relevant parameters (e.g., market share, price, etc.). The value of the underlying is modeled as a Geometric Brownian Motion, where the different sources of uncertainty are assumed to be independent. However, we argue that in the case of long-term projects like pharmaceutical R&D applying scenario planning is more appropriate for capturing uncertainty than using other quantitative forecasting techniques to develop a scenario tree. Thus, we focus on binomial lattices that implicitly aggregate multiple sources of uncertainty to different scenarios (e.g., best case vs. worst case). Therefore, problems of exactly specifying each source of uncertainty and specifying their correlation can be mitigated. Given our objective of practical validity and complexity reduction, we thus focus on the binomial modeling approach as in Cox et al. (1979) and Rendleman and Bartter (1979) who allows sequential decision problems to be analyzed in the simplest model setup. In this regard, our model can be classified as a heuristic approach because it assumes simplified distributions for the asset value of the derivative project. Thus, the number of possible states for the value of the derivative project is reduced, and thereby also the number of possible values of the compound option is limited.

2.2 Simplifying the arbitrage-based valuation of compound options

In this section, we demonstrate how the current valuation methodology of compound option models can be simplified. As we consider this methodological contribution of our work valid for any iterative multistage resource allocation process, we use common real option model terminology as established in prior work (Cox et al. 1979; Rendleman and Bartter 1979). However, in Sect. 3, we demonstrate the specific applicability of our model to valuing the Kellogg and Charnes (2000) example, thus turning to the specific R&D context.

In all (real) option models, the payoff of a single-fold call option is duplicated by investing in m (0 ≤ m ≤ 1) parts of the derivative project V and partly financing this investment by taking out a risk-free loan of B (B ≤ 0).Footnote 3 The strike price is I,Footnote 4 the risk-free interest rate is r f and the time to maturity is τ. Assuming complete and arbitrage-free markets (e.g., for a highly correlated surrogate asset), the value C t of the single-fold option is

$$ C_{t} \quad = \quad m\, \cdot \,V_{t} + B\quad = \quad \frac{{C_{t + 1}^{ + } - C_{t + 1}^{ - } }}{u - d} + \frac{{u\, \cdot \,C_{t + 1}^{ - } - d\, \cdot \,C_{t + 1}^{ + } }}{{(u - d)\cdot(1 + r_{f} )^{\tau } }}, $$
(1)

where

$$ \begin{aligned} &C_{t + 1}^{ + / - } = \hbox{max} [0,\;(V_{t + 1}^{ + / - } - I)], \hfill \\ &\quad {\text{with}}\quad V_{t + 1}^{ + } = V_{t} \cdot u,\quad V_{t + 1}^{ - } = V_{t} \cdot d\quad {\text{and}}\quad 0 < d < 1 < (1 + r_{f} ) < u, \hfill \\ \end{aligned} $$
(2)
$$ m_{t} \quad = \quad \;\frac{{C_{t + 1}^{ + } - C_{t + 1}^{ - } }}{{V_{t + 1}^{ + } - V_{t + 1}^{ - } }}\quad = \quad \frac{{C_{t + 1}^{ + } - C_{t + 1}^{ - } }}{{(u - d) \cdot V_{t} }} $$
(3)
$$ B_{t} \quad = \quad \;\frac{{C_{t}^{ - } \cdot V_{t + 1}^{ + } - C_{t + 1}^{ + } \cdot V_{t + 1}^{ - } }}{{(1 + r_{f} ) \cdot (V_{t + 1}^{ - } - V_{t + 1}^{ + } )}}\quad = \quad \frac{{u \cdot C_{t + 1}^{ - } - d \cdot C_{t + 1}^{ + } }}{{(u - d) \cdot (1 + r_{f} )}}. $$
(4)

A series of uncertain investments I 0, I 1, …, I n , can be valued as a compound option by recursively applying these formulas. For the following valuation of the compound option, we use the notation depicted in Fig. 2. C z,t is the value of a z-fold (compound) option at time t. More specifically, an investment in t = i can be considered an option to make an investment in the next round in t = i + 1, where the option is exercised only if the project value is greater than the investment I i+1 needed to continue the investment; otherwise, the project is abandoned (Lin 2002).

Fig. 2
figure 2

Valuing sequential investments as compound option (adapted from Lee et al. 2008: 48)

Full size image

In the first step, applying the current valuation methodology from the extant literature, the innermost option must be valued with an extended time to maturity from t 0 to t n . Extending the innermost option’s time to maturity is necessary to duplicate the twofold option by acquiring the (single-fold) innermost option and taking out a risk-free loan (also see Benaroch et al. 2006, who explicitly state this assumption). Then, in the second step, the value of the twofold compound option can be determined by forming a portfolio D 1,t of a single-fold option C 1,t in t that duplicates the payoff of the option in t + 1 by investing in m 1,t parts of the underlying and taking out a risk-free loan of B 1,t :

$$ D_{1,t} \quad \; = \quad m_{1,t} \cdot V_{t} + B_{1,t}. $$
(5)

Now, we consider a compound option C 2,t that represents an option on the option C 1,t . Applying the compound option methodology proposed in current literature, we can determine the value of the twofold compound option by forming the duplicating portfolio D 2,t , thus investing in m 2,t parts of the single-fold option C t and taking out a risk-free loan of B 2,t . However, the value of the single-fold option C t is duplicated by D 1,t [also see Eq. (5)]. Consequently, the payoff of the twofold compound option C 2,t can be duplicated by a portfolio which consists of the partially debt-funded acquisition of the single-fold option’s duplicating portfolio D 1,t . We call this stepwise duplication process the “indirect duplication”:

$$ D_{2,t} \quad = \quad m_{2,t} \cdot C_{1,t} + B_{2} \quad = \quad m_{2,t} \cdot D_{1,t} + B_{2}. $$
(6)

Applying the indirect duplication, which is the only method proposed in the current literature on real options (e.g., Copeland and Antikarov 2001), the valuation of a z-fold compound option requires a total of z computational steps, where in each computational step a binomial tree for the value of the layer of the compound option is derived.

Referring to the Kellogg and Charnes (2000) example, the indirect duplication requires a total of 6 computational steps to value the sixfold compound option. In each step, a binomial tree for each layer of the compound option has to be developed. In the first step, a binomial lattice for the value of the underlying project (considering the net payoffs) for the whole 12 periods (t = 0 to t = 12) needs to be developed (this is also depicted in the gray boxes in Fig. 5 in the appendix). Then, in the next step, the binomial tree for the second layer of the compound option needs be derived by taking into account the investment in t = 10 and calculating the net payoffs of the twofold compound option applying formula (2). This allows again applying formula (1) to calculate the value of the twofold option from t = 0 to t = 9. This procedure needs to be repeated in the following steps 3–6 to determine the value of the sixfold option, which is the R&D project. In our opinion, this methodology which is found in common text books (e.g., Copeland and Antikarov 2001) is not very straightforward especially when applied to higher-fold compound options (z > 2). However, within the very same set of assumptions (i.e., complete and arbitrage-free markets), we can reduce the multistep sequential duplication process to a single-step duplication process. Thus, we can derive the lattice that depicts the value of the z-fold compound option directly from the lattice depicting the value of the derivative project. Note that we have duplicated the single-fold option by taking out a risk-free loan and by acquiring part of the derivative project. Referring to Ross’s (1978) general analysis of duplicating uncertain income streams as linear combinations of traded assets, we can duplicate the twofold compound option by directly investing in m 2,t * parts of the derivative project and a higher relative amount of debt B 2,t *. We call this approach “direct duplication”:Footnote 5

$$ \begin{gathered} D_{2,t} = \quad m_{2,t} \cdot D_{1,t} + B_{2,t} \quad = \quad m_{2,t} \cdot \left[ {m_{1,t} \cdot V_{t} + B_{1,t} } \right] + B_{2,t} \hfill \\ \quad \quad \;\;{\kern 1pt} = \quad m_{2,t}^{*} \cdot V_{t} + B_{2,t}^{*} \;,\quad {\kern 1pt} with\quad m_{2,t}^{*} \;\; = \quad m_{1,t} \cdot m_{2,t} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} B_{2,t}^{*} \;\;{\kern 1pt} {\kern 1pt} = \quad m_{2,t} \cdot B_{1,t} \; + \;B_{2,t}. \hfill \\ \end{gathered} $$
(7)

In this approach, the duplicating portfolio of the single-fold option D 1,t is a linear combination of a risk-free loan B and the acquisition of m shares of the underlying. The duplicating portfolio of the twofold compound option D 2,t again is a linear combination of D 1,t and a risk-free loan. D 2,t can thus be directly modeled as a linear combination of the original underlying and a risk-free loan. In this line of reasoning, Garman (1976) noted that the value of any compound option is a piecewise linear function of the value of the derivative project. By induction, the direct valuation can be generalized to a valuation of any z-fold compound option. This means that any z-fold compound option can be valued by forming a duplicating portfolio of m z,t * parts of the underlying and a risk-free loan of B z,t *, where

$$ m_{z,t}^{*} \;\; = \quad \prod\limits_{i = 1}^{z} {m_{i,t} } ,\,{\text{and}} $$
(8)
$$ B_{z,t}^{*} \;\; = \quad B_{{{\text{z}} - 1,t}}^{*} \cdot m_{{{\text{z}},t}}^{*} + B_{{{\text{z}},t}} ,\,{\text{that can be reformulated as}} $$
(9)
$$ B_{z,t}^{*} = \sum\limits_{l = 1}^{z} {B_{l,t} \cdot \prod\limits_{i = l + 1}^{z} {m_{i,t} } } . $$

The parameter m z,t *, which represents the acquired part of the derivative project, is the product of all fold-specific parts m i,t of the fold-specific underlying, which is an (i−1)-fold (compound) option (or the derivative project if i = 1). Given that 0 ≤ m i,t  ≤ 1, the part of the derivative project that needs to be acquired to form a duplicating portfolio decreases in the fold number z. B z,t* can be calculated as sum of m z,t parts of B z−1,t * (that is the amount of risk-free loan of the duplicating portfolio of the (z−1)-fold compound option) and the increment of an additional risk-free loan.Footnote 6 Thus, by increasing the number of stages in a sequential investment project from (z−1) to z, an increment B z,t of debt is added to finance the acquisition of (part of) the derivative underlying when forming the duplicating portfolio. Consequently, the fraction of irreversibly committed option premium decreases. This has interesting implications for the valuation of compound options: The valuation of any compound option can be computed in a single step by directly forming a duplicating portfolio consisting of the derivative project and a risk-free loan. Directly duplicating a z-fold compound option requires applying Eqs. (1) to (6) and using the derivative project (and a risk-free loan) in Eqs. (5) and (6) instead of the duplicating portfolio of the (z−1)-fold compound option as we will demonstrate in Sect. 3.

Most importantly, the direct duplication and the indirect valuation are mathematically equivalent and thus yield the exact same results; however, the direct duplication does not require any additional and more restrictive assumptions compared to the indirect duplication. We simply refer to the perfect markets assumption and the absence of cash flows before the project is completed, as in the case of indirect duplication. Overall, the direct duplication of a compound option is a methodological simplification that requires fewer computational steps than prior approaches; furthermore, no complexity reduction versus loss-of-accuracy tradeoff exists. The heuristic characteristic of our approach thus lies in the assumption of a simplified binomial distribution for the asset value of the underlying project which leads to a reduced complexity.

3 Applying the direct duplication approach to R&D

3.1 The Kellogg and Charnes (2000) example as a binomial compound option

In this section, we apply the direct duplication approach to the Kellogg and Charnes (2000) NDA example, thus demonstrating the applicability of our approach in a real-world context. Furthermore, we can compare our approach to existing models referring to the very same example, and assess the practical validity of the different approaches. Note that Kellogg and Charnes (2000) do not present a compound option approach, while Cassimon et al. (2004) compute an analytical extension of the Geske (1979) model. The latter approach thus requires sophisticated modeling in Mathematica™ and does not offer an intuitive algorithm that allows management to check the plausibility of the computed results. However, our approach allows directly duplicating the compound option with just standard spreadsheet calculation programs (e.g., MS Excel™) and thus enables management to comprehend the necessary computational steps.

As in Kellogg and Charnes (2000), we assume Cox et al. (1979) parameters u = 1.30 and d = 0.77 and a risk-free rate r = 7.09 % for our analysis. The value of the derivative project in every node of the lattice can be determined with the following equation:

$$ V_{n}^{ + / - } \quad = \quad V_{0} \; \cdot \;u^{n - m} \; \cdot \;d^{m} , $$
(10)

where (n−m) (0 ≤ m ≤ n) is the total number of realizations of the growth factor u, while m is the number of realizations of factor d.

Using these values as inputs, we obtain a value for the sixfold compound option in t = 0 of 59,958 thousand US$. Note that our direct approach requires only a single computational step which allows the calculation to be depicted in a single spreadsheet; this would not be possible applying the standard indirect approach. Figure 5 in Appendix A shows the detailed spreadsheet (the MS Excel™ sheet containing all formulae is also provided as supplementary material to this article). Given that the option premium (costs in t = 0) is 2,200 thousand US$, it is beneficial to acquire the real option and initiate the R&D project.

To further illustrate the direct duplication methodology, we examine the valuation of the last two stages of the project development process as a twofold compound option. Figure 3 depicts this sublattice.Footnote 7 The gray boxes depict the development of the value of the derivative project, excluding investments I t , to keep the project alive. For example, in t = 10, an investment of I 10 = 3,300 is required to start the FDA filing phase, which takes another 2 years. In the best case (the upper path of the binomial lattice), the value of the R&D project increases to 2,877,759, resulting in a net payoff value of 2,156,699 from the subsequent commercialization (these values are also taken from Kellogg and Charnes (2000); in their study, the (reasonable) investment for the commercialization depends on the (gross) payoff of the R&D project, which seems a realistic assumption to us).Footnote 8 From the different payoff scenarios in t = 12, the value of the (single-fold) option in t = 11 and t = 10 can be calculated by applying Eq. (1). In t = 10, management needs to decide about investment I 10: a rational R&D manager will invest an additional 3,300—thus exercising the twofold compound option from the clinical phase 3—only if the value of the underlying single-fold option is higher than the required investment [the exercise decision is thus represented by Eq. (2)]. In the best-case scenario in t = 10, the value of the project is 1,702,616, and the value of the single-fold real option is 1,275,742 (see Fig. 3). Subtracting the exercise price of the twofold compound option of 3,300 results in a 1,272,442 net payoff for the twofold compound option. In this manner, we can calculate all possible (net) payoffs for the twofold compound option.

Fig. 3
figure 3

Binomial lattice of the drug development process

Full size image

To determine the value of the twofold compound option in t = 9, we need to duplicate its payoffs from the duplicating portfolio. Applying the indirect valuation methodology suggested in existing literature on binomial compound option modeling requires a valuation of the single-fold option with an extended time to maturity from t = 0 to t = 12. This step is necessary to form a duplicating portfolio of the twofold compound option. In the next step, it is necessary to model (and value) the lattice of the twofold compound option from t = 0 to its time to maturity (t = 10), to build a duplicating portfolio of the threefold compound option and so on. Thus, z lattices must be modeled to finally derive the lattice that depicts the value of the z-fold compound option. However, with our suggested methodology, we can directly duplicate any compound option by acquiring part of the derivative project and a risk-free loan. In t = 9, in the best-case scenario, the payoff of the twofold compound option can be directly duplicated by acquiring 0.7498 parts of the derivative asset and taking out a risk-free loan of −3,990.8254:

$$ \begin{gathered} 0.7498 \cdot 1{,}702{,}816 + ( - 3{,}990.8254) \cdot 1.0709\quad = \quad 1{,}272{,}442 \hfill \\ 0.7498 \cdot 1{,}008{,}754 + ( - 3{,}990.8254) \cdot 1.0709\quad = \quad 752{,}057 \hfill \\ \end{gathered}. $$

Thus, the value of the option is 978,098:

$$ 0.7498 \cdot 1{,}309{,}858 + ( - 3{,}990.8254)\quad = \quad 978{,}098. $$

With the R&D project progressing over time, the binomial tree becomes smaller as development paths that were not realized can be excluded from the analysis. This also allows updating information on the R&D project in case a project manager finds that assumptions of previous calculations were not accurate.

3.2 Leverage of the duplicating portfolio as measure of commitment

Given that R&D investments are highly irreversible (Goel and Ram 2001; Pindyck 1991), the investments made up to a given point in time determine the firms “commitment” to the project (Bremser and Barsky 2004; Ghemawat 1991; Sull 2003). We define commitment in a broad sense as all valuable resources irreversibly dedicated to a certain R&D project. However, by investing sequentially, the initial commitment is reduced, and further investments can be deferred until uncertainty has resolved and new information about the R&D project is available. The more the sequence of investments is staged, the lower ceteris paribus the initial investment necessary to start the project while the time between two investment payments decreases (given that the project’s total time to completion remains unchanged). However, most projects require a “minimal investment rate” that must be sustained to keep the project alive (Mölls and Schild 2012). Consequently, there are certain limits to increasing the sequentiality of the investment process.

To analyze the effects of staging on the firm’s propensity to make further investments in a real option setting, a measure of commitment is needed. Generally, the more the investments are staged (i.e., with higher sequentiality), the lower ceteris paribus the commitment to the project at a certain point in time. We therefore suggest the “leverage of the duplicating portfolio” as a measure of the firm’s commitment to a given series of investments. Smith (2007) proposes the amount of up-front investment relative to the total investment required to complete the project as a measure of an investment project’s sequentiality, and thus its commitment. Smith’s (2007) approach is thus input-oriented, as it solely depends on the investments I t . However, we think that a measure reflecting how much the firm has already invested relative to the current market value of its real option is more informative, as the market value determines the firm’s propensity to make further investments. We therefore differ from Smith’s (2007) approach and suggest the leverage of the duplicate portfolio as a market value-based measure of the sequentiality of the R&D project. The leverage not only considers how much additional investment is needed but also how uncertainty has resolved over time. The leverage of the duplicating portfolio and the commitment to the R&D project are inversely related; the higher the leverage, the lower ceteris paribus the commitment. The leverage thus reflects how the commitment develops over time depending on the progress of the project. We therefore define the leverage of the duplicating portfolio L z,t as the proportion B z,t * of the risk-free loan in acquiring m z,t * shares of the underlying asset with a value of V t (see Naik and Uppal 1994 for a similar formulation):

$$ \begin{aligned} L_{z,t} &= \frac{{\left| {B_{z,t}^{*} } \right|}}{{m_{z,t}^{*} \cdot V_{t} }} \hfill \\ &= \frac{{ - \sum\limits_{l = 1}^{z} {B_{l,t} \cdot \prod\limits_{i = l + 1}^{z} {m_{i,t} } } }}{{\prod\limits_{i = 1}^{z} {m_{i,t}^{{}} } \;\; \cdot \;\;V_{t} }} \hfill \\ \end{aligned}. $$
(11)

Expression (m z,t *· V t ) can be interpreted as the (gross) total value of the duplicating portfolio, with B z,t * the amount funded by a risk-free loan. Similar to a debt-funded firm, the ratio of both expressions can be denoted as the leverage ratio of the portfolio (note that L must not be confused with the leverage of the firm for valuing an option on the equity of a debt-funded firm in Geske’s (1979) model). The leverage is thus complement to the “equity ratio,” which reflects the (relative) amount of irreversible investments made up to a certain point in time or, in other words, the commitment to the R&D project. Therefore, the leverage and the commitment are inversely related. Thus, given the sequentially of the R&D project in our example, a levered position corresponds to a weaker commitment to continuing the project because the sunk costs, which are the irreversibly committed investment payments that have already been spent on the project, are low relative to the (gross) project value.

Overall, the leverage ratio L mirrors important aspects of sequential versus unstaged investment projects. First, as the number of stages of the investment increases, the leverage ratio of the compound option also increases (ceteris paribus). This reflects the relatively lower initial capital investment of sequential investment projects compared to complete irreversible up-front financed projects that inevitably have an (implicit) leverage of zero. Second, this lower initial capital investment has a risk-reducing effect since losses are limited to the option premium(s), that is, prior investment outlays. Sequential investment projects can thus be characterized as low-commitment (R&D) strategies (see Klingebiel and Adner 2012) or as “exploratory investments” (Bar-Ilan and Strange 1998) as the staging of investments implies varying degrees of commitment. Consequently, the leverage of the duplicating portfolio is a market-based operationalization of the (resource) commitment construct, and might be used as such also in future empirical research studies.

We can now illustrate how the leverage of the duplicating portfolio develops in the example from Cassimon, Engelen, Thomassen, and van Wouwe (2004) and Kellogg and Charnes (2000). The leverage depends on (1) the series of investments made (their impact is similar to Smith 2007) but also on (2) the value of the derivative project. If a project develops favorably, further investments are made, and the value of the derivative project increases. We therefore would expect a continuous decline of the leverage that reflects the increased commitment over time.

Figure 4 illustrates the leverage L (red line) for the best-case path of the R&D project (the upper path in the binomial lattice, see Fig. 5 in Appendix A) where in any sub-period a value increase (u) is realized. The points in time when further investments I t are required to keep the project running are marked with a cross. The investments obviously lead to a decrease in the leverage that reflects the increased commitment. Figure 4 also illustrates that even in periods when no investments are made, the leverage still decreases. This can be explained by the positive development of the “market value” of the R&D project. We consider this a methodological advantage as Smith’s (2007) measure for the “degree of sequentiality” depicts only the amount of investments made up to a certain point in time, relative to the total investments needed to complete the project. This measure is independent of the progress of the project and therefore does not truly capture the firm’s propensity to make further investments.

Fig. 4
figure 4

L, m*, and B* of the duplicating portfolio in the best-case path

Full size image
Fig. 5
figure 5

Sixfold compound option value

Full size image

To supplement the discussion of the option’s leverage, Fig. 4 also visualizes in addition to L the parameters m* and the absolute amount of B* of the duplicating portfolio, again in the best-case path, as the number of periods goes from 1 to 11 (m* and B* can only be determined for t = n−1). While m* remains almost at the same level,Footnote 9 the development of the absolute amount of debt B* decreases over time which is one factor in the decrease of the leverage L (the other being the increasing value of the underlying project). Furthermore, note that a significant decrease of B* occurs at those points in time where additional capital infusions are made (e.g., t = 7). Thus, the increasing commitment is also reflected in the substitution of debt for equity.

3.3 Implementing the model in corporate R&D management

We developed our proposed binomial model, answering the call of Hartmann and Hassan (2006), who emphasize the need to “boost acceptance” of the real options approach in corporate practice. In this context, it is crucial that a valuation methodology can be easily implemented in corporate R&D management (Triantis 2005). The implementation of our model requires the following procedure, using standard spreadsheet calculation programs such as MS Excel™. First, the multiplicative binomial tree has to be modeled for the entire duration of the project. Most challenging is estimating the parameters u and d, as the option value is highly sensitive to their specification. However, possible development paths for the value of the underlying R&D project can be derived using scenario planning techniques (Miller and Waller 2003). Second, the necessary investments need to be estimated as well as the specific points in time where these capital infusions become necessary. These investments determine the time to maturity of each compound option and can be obtained from the R&D project plan. Third, the risk-free interest rate can be derived from the yield of government bonds with an equivalent maturity date. These input parameters given, the value of the z-fold compound option can be calculated recursively, starting with the innermost option that must be valued for the time period between the last two investment payments applying Eqs. (1) to (4). In our NDA example, the innermost option thus must be valued from t = 10 to t = 12 (also see Fig. 3). Next, the value of the twofold compound option on the innermost option is calculated. The possible payoffs of the twofold compound option are determined by comparing the innermost option’s value to the investment payment necessary to acquire the innermost option. This requires substituting the value of the innermost option for V t in Eq. (2). Again, in our example, the investment to acquire the innermost option is 3,300 (in thousands), whereas the innermost option’s value depends on the progress of the R&D project (see Figs. 3 and 6). Next, the value of the threefold compound option, whose underlying is the twofold option, is computed accordingly. Applying this recursive valuation methodology, the value of any z-fold compound option can be calculated in a single binomial tree (see Fig. 5 in appendix A), thus requiring only a single computational step. The calculation can be depicted in a single spreadsheet, which can be used as a “graphic user interface” (also see Ghosh and Marvin 2012). Note that these “steps” for implementing the model listed above must not be confused with the number of computational steps, which is just one in the case of our direct duplication. Applying the sequential duplication proposed in current literature requires calculating each of the compound option’s z layers starting from t = 0, resulting in a total of z computational steps.

Overall, for implementation issues, our proposed model reduces valuation complexity and thus allows for a more user-friendly graphic “interface.” In this context, our approach builds upon generally accepted tools in R&D management, including commonly used spreadsheet programs (i.e., MS Excel™) and scenario planning. This is often a key requirement for implementation in corporate practice.

4 Discussion and conclusion

In this paper, we proposed an approach to modeling sequential compound options inherent in R&D projects by applying binomial lattice techniques. We argue that our binomial approach to modeling sequential compound options enhances the practical validity of the real options approach (1) by reducing the mathematical complexity compared to continuous-time analytical option pricing models, (2) by significantly reducing the number of computational steps to value a z-fold compound option from z steps (as in prior binomial approaches) to just one step, and (3) using an approach that mirrors the iterative multistage resource allocation process of sequential investment analysis, thus potentially increasing managers’ awareness of option-like rights (Driouchi and Bennett 2011). Note that (correctly) valuing real options requires an awareness of option-like rights in the first place. Furthermore, our approach shifts focus from a single initial R&D investment decision to effectively exercising the subsequent investment options (to continue the R&D project). In this context, we present the market-based leverage as a measure of the firm’s commitment to a given series of R&D investments. The leverage measure illustrates the risk-reducing effects of sequential investment projects to management, thus mitigating underinvestment problems.

There are several limitations to our suggested approach. Most of these limitations are closely related to the real options approach in general and are thus not model-specific. Most importantly, we have emphasized that in the case of R&D, no (perfect) market for trading such a unique “asset” exists. This is an inherent limitation of the real options approach that needs to be considered when applying the methodology in corporate practice. However, prior literature states that a highly correlated tradable asset can serve as a surrogate when forming a duplicating portfolio. Furthermore, the use of discrete-time binomial models comes at the cost of imposing a simplified distribution of the asset value. Estimating the parameters u and d is thus challenging, as the option value is highly sensitive to their specification. However, the same argument applies to the variance in the (analytical) models of Black and Scholes (1973) and Geske (1979). We also have to admit that we cannot ultimately predict the potential acceptance of our approach in corporate practice. However, as demonstrated in Verbeeten’s (2006) study, highly uncertain environments increase firms’ willingness to adopt more sophisticated capital budgeting practices. As R&D is typically associated with high levels of uncertainty, we think that implementing our approach is most likely in R&D management (also see Hartmann and Hassan 2006). Also note that although we use the example of NDA valuation, our proposed compound option model works in any iterative multistage resource allocation process. For example, valuing start-up firms whose business-model mainly builds upon R&D (e.g., biotech firms) shares many features with R&D valuation. We thus suggest that our approach can also be applied in future research to valuing such companies, whose lead R&D compound accounts for the key value driver.